人教版数学九年级上册:24.2.2 直线和圆的位置关系-课件(共18张ppt)
文档属性
| 名称 | 人教版数学九年级上册:24.2.2 直线和圆的位置关系-课件(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 21:40:40 | ||
图片预览





文档简介
(共18张PPT)
切
线
的
判
定
24.2.2直线与圆的位置关系
只要你认真听完今天的课你就会明白!
问题
1
当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2
砂轮打磨工件飞出火星的方向是什么方向?
[学习目标]
1.理解切线的判定定理,会准确过圆上一点画圆的切线;
2.会用圆的切线判定定理进行简单的证明.
3.
在解决问题中培养分析问题和解决问题的能力,总结常用辅助线的做法.
预习反馈:
优秀小组:
第3组、第6组、
优秀个人:
赵钰佳、张珂馨、
杨晓杰、陈丽坤、
樊筱玉、杨志伟
存在的问题:
1、概念理解不到位;
2、审题不够仔细;
3、书写不规范。
2.直线和圆的位置关系可以通过哪些方法判断呢?
预习案:
(1)直线和圆公共点个数;
(2)数量关系:d与r的大小关系.
3.请你根据上述方法,分析直线和圆相切的判断方法:
(1)直线和圆公共点个数:只有一个公共点时;
(2)数量关系:
d=r
.
1.直线和圆的位置关系有几种?
①相交
②相切
③相离
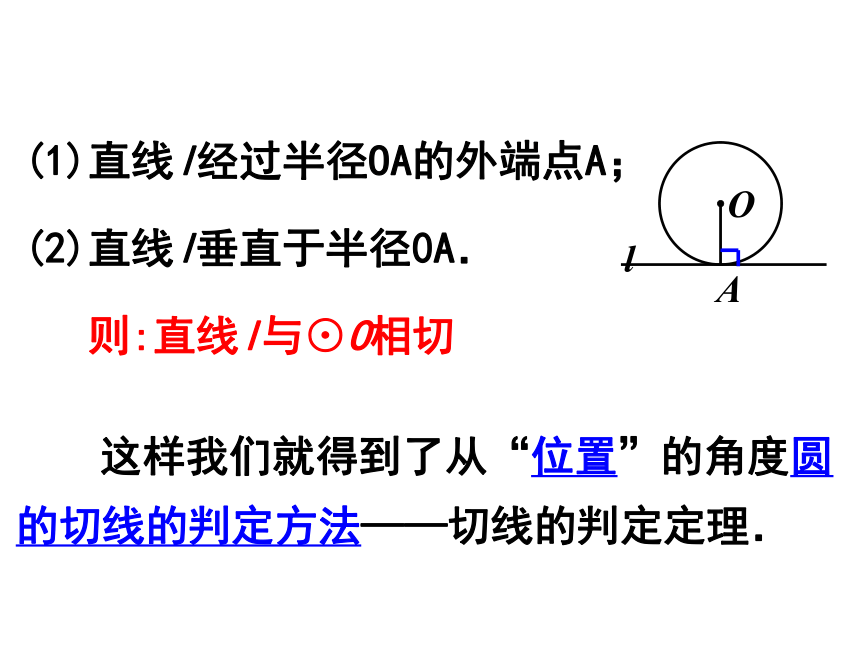
(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切
这样我们就得到了从“位置”的角度圆的切线的判定方法——切线的判定定理.
A
O
l
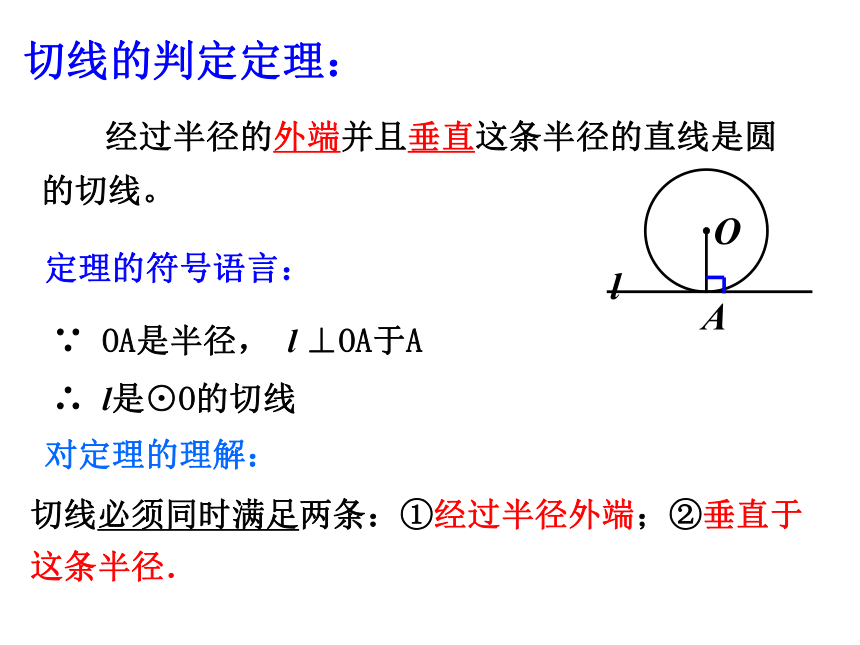
切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解:
切线必须同时满足两条:①经过半径外端;②垂直于
这条半径.
A
O
l
定理的符号语言:
∵
OA是半径,
l
⊥OA于A
∴
l是⊙O的切线
1、判断:
(1)过半径的外端的直线是圆的切线(
)
(2)与半径垂直的的直线是圆的切线(
)
(3)过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线.
2.圆的切线必须同时满足两个条件:
①经过半径外端;②垂直于这条半径.
1.判定直线与圆相切有三种方法?
如图,已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,
所以连接OC,只要证明AB⊥OC即可。
如图,
为等腰三角形,O是底边BC
的中点,腰AB与⊙O相切于点D.
求证:AC是⊙O的切线.
O
B
A
C
探究一、二的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直.简记为:有交点,连半径,证垂直.
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长.简记为:无交点,作垂直,证半径.
1、切线的判定方法;
2、切线的作法;
3、常见辅助线.
(1)当直线与圆有公共点时,简说成“连半径,证垂直”;
(2)当直线与圆没有公共点时,简说成“作垂直,证半径”
课堂小结
当堂检测:
1.下列说法正确的是(
)
A.与圆有公共点的直线是圆的切线.
B.和圆心距离等于圆的半径的直线是圆的切线;
C.垂直于圆的半径的直线是圆的切线;
D.过圆的半径的外端的直线是圆的切线
当堂检测:
2.
已知:AB是⊙O的直径,∠ABT=45°,
AT=AB.
求证:AT是⊙O的切线.
证明:∵AB=AT,∠ABT=45°
∴∠ATB=∠ABT=45°
∴∠TAB=180°-∠ABT-∠ATB=90°
∴AT⊥AB,
即AT是⊙O的切线.
当堂检测:
3.已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°.
求证:直线AB是⊙O的切线.
不经历风雨,怎么见彩虹
没有人能随随便便成功!
能力提升
1、如图,AB是⊙O的直径,O为圆心,AD、BD是圆的弦,且∠PDA=∠PBD。直线PD是⊙O的切线吗?请说明理由。
切
线
的
判
定
24.2.2直线与圆的位置关系
只要你认真听完今天的课你就会明白!
问题
1
当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2
砂轮打磨工件飞出火星的方向是什么方向?
[学习目标]
1.理解切线的判定定理,会准确过圆上一点画圆的切线;
2.会用圆的切线判定定理进行简单的证明.
3.
在解决问题中培养分析问题和解决问题的能力,总结常用辅助线的做法.
预习反馈:
优秀小组:
第3组、第6组、
优秀个人:
赵钰佳、张珂馨、
杨晓杰、陈丽坤、
樊筱玉、杨志伟
存在的问题:
1、概念理解不到位;
2、审题不够仔细;
3、书写不规范。
2.直线和圆的位置关系可以通过哪些方法判断呢?
预习案:
(1)直线和圆公共点个数;
(2)数量关系:d与r的大小关系.
3.请你根据上述方法,分析直线和圆相切的判断方法:
(1)直线和圆公共点个数:只有一个公共点时;
(2)数量关系:
d=r
.
1.直线和圆的位置关系有几种?
①相交
②相切
③相离
(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切
这样我们就得到了从“位置”的角度圆的切线的判定方法——切线的判定定理.
A
O
l
切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解:
切线必须同时满足两条:①经过半径外端;②垂直于
这条半径.
A
O
l
定理的符号语言:
∵
OA是半径,
l
⊥OA于A
∴
l是⊙O的切线
1、判断:
(1)过半径的外端的直线是圆的切线(
)
(2)与半径垂直的的直线是圆的切线(
)
(3)过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线.
2.圆的切线必须同时满足两个条件:
①经过半径外端;②垂直于这条半径.
1.判定直线与圆相切有三种方法?
如图,已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,
所以连接OC,只要证明AB⊥OC即可。
如图,
为等腰三角形,O是底边BC
的中点,腰AB与⊙O相切于点D.
求证:AC是⊙O的切线.
O
B
A
C
探究一、二的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直.简记为:有交点,连半径,证垂直.
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长.简记为:无交点,作垂直,证半径.
1、切线的判定方法;
2、切线的作法;
3、常见辅助线.
(1)当直线与圆有公共点时,简说成“连半径,证垂直”;
(2)当直线与圆没有公共点时,简说成“作垂直,证半径”
课堂小结
当堂检测:
1.下列说法正确的是(
)
A.与圆有公共点的直线是圆的切线.
B.和圆心距离等于圆的半径的直线是圆的切线;
C.垂直于圆的半径的直线是圆的切线;
D.过圆的半径的外端的直线是圆的切线
当堂检测:
2.
已知:AB是⊙O的直径,∠ABT=45°,
AT=AB.
求证:AT是⊙O的切线.
证明:∵AB=AT,∠ABT=45°
∴∠ATB=∠ABT=45°
∴∠TAB=180°-∠ABT-∠ATB=90°
∴AT⊥AB,
即AT是⊙O的切线.
当堂检测:
3.已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°.
求证:直线AB是⊙O的切线.
不经历风雨,怎么见彩虹
没有人能随随便便成功!
能力提升
1、如图,AB是⊙O的直径,O为圆心,AD、BD是圆的弦,且∠PDA=∠PBD。直线PD是⊙O的切线吗?请说明理由。
同课章节目录
