北师大版数学九年级上册:6.3.2 反比例函数与一次函数综合 导学案(含答案)
文档属性
| 名称 | 北师大版数学九年级上册:6.3.2 反比例函数与一次函数综合 导学案(含答案) | 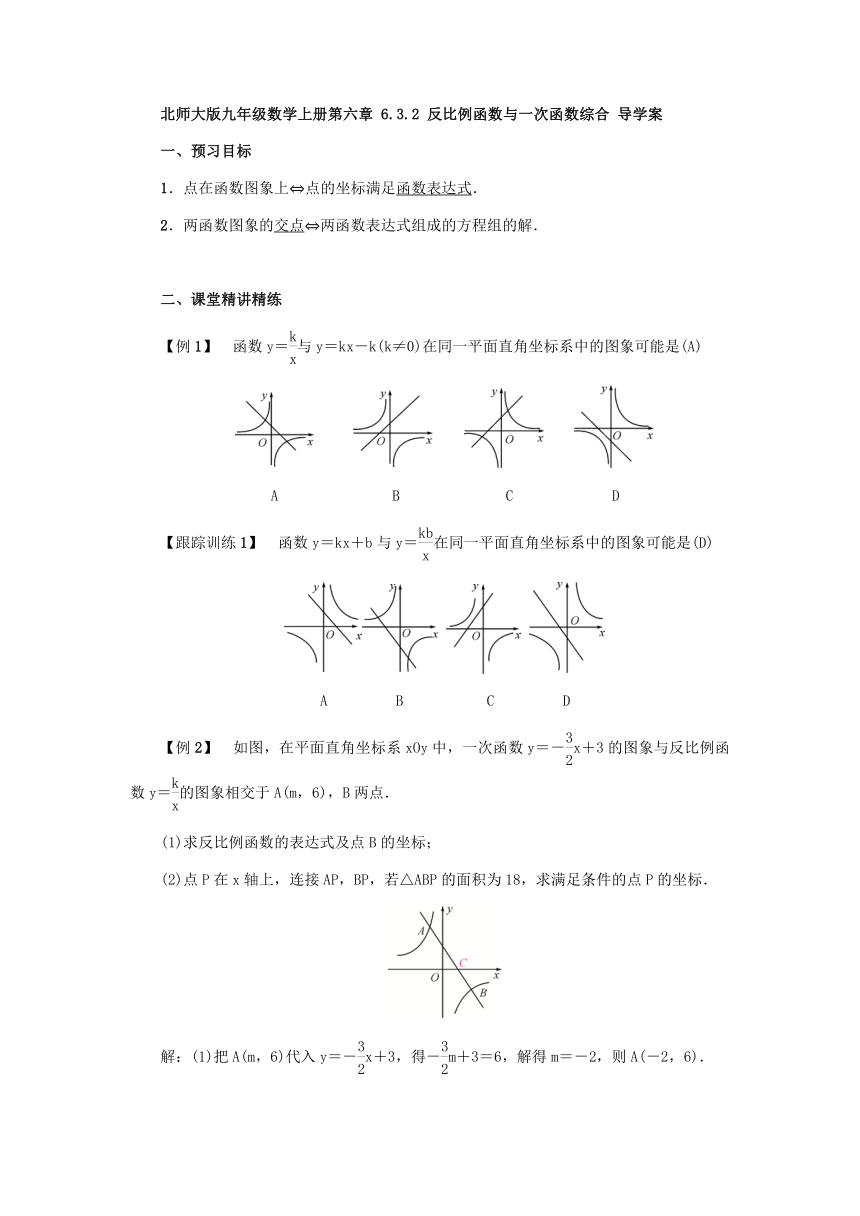 | |
| 格式 | docx | ||
| 文件大小 | 88.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 10:42:08 | ||
图片预览


文档简介
北师大版九年级数学上册第六章
6.3.2
反比例函数与一次函数综合
导学案
一、预习目标
1.点在函数图象上?点的坐标满足函数表达式.
2.两函数图象的交点?两函数表达式组成的方程组的解.
二、课堂精讲精练
【例1】 函数y=与y=kx-k(k≠0)在同一平面直角坐标系中的图象可能是(A)
A
B
C
D
【跟踪训练1】 函数y=kx+b与y=在同一平面直角坐标系中的图象可能是(D)
A
B
C
D
【例2】 如图,在平面直角坐标系xOy中,一次函数y=-x+3的图象与反比例函数y=的图象相交于A(m,6),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)点P在x轴上,连接AP,BP,若△ABP的面积为18,求满足条件的点P的坐标.
解:(1)把A(m,6)代入y=-x+3,得-m+3=6,解得m=-2,则A(-2,6).
把A(-2,6)代入y=,得k=-2×6=-12.
∴反比例函数的表达式为y=-.
联立解得或
∴B点坐标为(4,-3).
(2)设y=-x+3与x轴的交点为C,则C(2,0),
设P(t,0),∵S△APC+S△BPC=S△ABP,
∴×|t-2|×6+×|t-2|×3=18,
解得t=6或t=-2,
∴P点坐标为(6,0)或(-2,0).
【跟踪训练2】 如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A,B两点,其中点A的坐标为(-1,4),点B的坐标为(4,n).
(1)根据图象,直接写出满足k1x+b>的x的取值范围;
(2)求这两个函数的表达式;
(3)点P在线段AB上,且S△AOP∶S△BOP=1∶2,求点P的坐标.
解:(1)x<-1或0<x<4.
(2)把A(-1,4)代入y=,得4=,解得k2=-4,
∴反比例函数的表达式为y=.
∴B(4,-1).
把A(-1,4),B(4,-1)代入y=k1x+b,得
解得
∴一次函数的表达式为y=-x+3.
(3)设AB与y轴交于点C.
∵点C在直线y=-x+3上,∴C(0,3).
∵S△AOB=OC·(|xA|+|xB|)=×3×(1+4)=7.5,S△AOP∶SBOP=1∶2,∴S△AOP=2.5.
∵S△AOC=×3×1=1.5,∴S△COP=2.5-1.5=1.
又∵OC=3,∴×3·xP=1,xP=.
把xP=代入y=-x+3,得yP=.
∴P(,).
三、课堂巩固训练
1.如图,一次函数y=kx-3的图象与反比例函数y=的图象交于A,B两点,其中A点坐标为(2,1),则k,m的值为(C)
A.k=1,m=2
B.k=2,m=1
C.k=2,m=2
D.k=1,m=1
2.如图,一次函数y1=ax+b和反比例函数y2=的图象交于A(-2,m),B(1,n)两点.若y1<y2,则x的取值范围是(D)
A.x>-2
B.x<-2或x>1
C.-2<x<1
D.-2<x<0或x>1
3.如图,已知点A(4,a),B(-10,-4)是一次函数y=kx+b图象与反比例函数y=图象的交点,且一次函数与x轴交于C点.
(1)求该反比例函数和一次函数的表达式;
(2)连接AO,BO,求△AOB的面积.
解:(1)∵点A(4,a),B(-10,-4)是一次函数y=kx+b图象与反比例函数y=图象的交点,
∴-4=.∴m=40.
∴反比例函数的表达式为y=.
把A(4,a)代入y=,得a==10,∴A(4,10).
把A(4,10),B(-10,-4)代入y=kx+b,得
解得
∴一次函数的表达式为y=x+6.
(2)在y=x+6中,令y=0,得x=-6,
∴C(-6,0).
∴S△AOB=S△AOC+S△BOC=×6×10+×6×4=42.
课堂总结
1.解决反比例函数与一次函数的综合问题,通常联立两个函数表达式,求方程组的解来确定交点坐标,也可将交点坐标代入两个表达式,求表达式中的待定系数.
2.在同一平面直角坐标系中,利用图象可以直观地比较几个函数值的大小,函数图象的相对位置高低与函数值的大小等价,图象在上方的,函数值较大.
3.解决反比例函数与一次函数图象交点个数问题,应联立两个函数表达式,构造一元二次方程,根据根的判别式判断交点情况,具体如下:①当Δ>0时,两个函数图象有两个交点;②当Δ=0时,两个函数图象有且只有一个交点:③当Δ<0时,两个函数图象没有交点.
6.3.2
反比例函数与一次函数综合
导学案
一、预习目标
1.点在函数图象上?点的坐标满足函数表达式.
2.两函数图象的交点?两函数表达式组成的方程组的解.
二、课堂精讲精练
【例1】 函数y=与y=kx-k(k≠0)在同一平面直角坐标系中的图象可能是(A)
A
B
C
D
【跟踪训练1】 函数y=kx+b与y=在同一平面直角坐标系中的图象可能是(D)
A
B
C
D
【例2】 如图,在平面直角坐标系xOy中,一次函数y=-x+3的图象与反比例函数y=的图象相交于A(m,6),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)点P在x轴上,连接AP,BP,若△ABP的面积为18,求满足条件的点P的坐标.
解:(1)把A(m,6)代入y=-x+3,得-m+3=6,解得m=-2,则A(-2,6).
把A(-2,6)代入y=,得k=-2×6=-12.
∴反比例函数的表达式为y=-.
联立解得或
∴B点坐标为(4,-3).
(2)设y=-x+3与x轴的交点为C,则C(2,0),
设P(t,0),∵S△APC+S△BPC=S△ABP,
∴×|t-2|×6+×|t-2|×3=18,
解得t=6或t=-2,
∴P点坐标为(6,0)或(-2,0).
【跟踪训练2】 如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A,B两点,其中点A的坐标为(-1,4),点B的坐标为(4,n).
(1)根据图象,直接写出满足k1x+b>的x的取值范围;
(2)求这两个函数的表达式;
(3)点P在线段AB上,且S△AOP∶S△BOP=1∶2,求点P的坐标.
解:(1)x<-1或0<x<4.
(2)把A(-1,4)代入y=,得4=,解得k2=-4,
∴反比例函数的表达式为y=.
∴B(4,-1).
把A(-1,4),B(4,-1)代入y=k1x+b,得
解得
∴一次函数的表达式为y=-x+3.
(3)设AB与y轴交于点C.
∵点C在直线y=-x+3上,∴C(0,3).
∵S△AOB=OC·(|xA|+|xB|)=×3×(1+4)=7.5,S△AOP∶SBOP=1∶2,∴S△AOP=2.5.
∵S△AOC=×3×1=1.5,∴S△COP=2.5-1.5=1.
又∵OC=3,∴×3·xP=1,xP=.
把xP=代入y=-x+3,得yP=.
∴P(,).
三、课堂巩固训练
1.如图,一次函数y=kx-3的图象与反比例函数y=的图象交于A,B两点,其中A点坐标为(2,1),则k,m的值为(C)
A.k=1,m=2
B.k=2,m=1
C.k=2,m=2
D.k=1,m=1
2.如图,一次函数y1=ax+b和反比例函数y2=的图象交于A(-2,m),B(1,n)两点.若y1<y2,则x的取值范围是(D)
A.x>-2
B.x<-2或x>1
C.-2<x<1
D.-2<x<0或x>1
3.如图,已知点A(4,a),B(-10,-4)是一次函数y=kx+b图象与反比例函数y=图象的交点,且一次函数与x轴交于C点.
(1)求该反比例函数和一次函数的表达式;
(2)连接AO,BO,求△AOB的面积.
解:(1)∵点A(4,a),B(-10,-4)是一次函数y=kx+b图象与反比例函数y=图象的交点,
∴-4=.∴m=40.
∴反比例函数的表达式为y=.
把A(4,a)代入y=,得a==10,∴A(4,10).
把A(4,10),B(-10,-4)代入y=kx+b,得
解得
∴一次函数的表达式为y=x+6.
(2)在y=x+6中,令y=0,得x=-6,
∴C(-6,0).
∴S△AOB=S△AOC+S△BOC=×6×10+×6×4=42.
课堂总结
1.解决反比例函数与一次函数的综合问题,通常联立两个函数表达式,求方程组的解来确定交点坐标,也可将交点坐标代入两个表达式,求表达式中的待定系数.
2.在同一平面直角坐标系中,利用图象可以直观地比较几个函数值的大小,函数图象的相对位置高低与函数值的大小等价,图象在上方的,函数值较大.
3.解决反比例函数与一次函数图象交点个数问题,应联立两个函数表达式,构造一元二次方程,根据根的判别式判断交点情况,具体如下:①当Δ>0时,两个函数图象有两个交点;②当Δ=0时,两个函数图象有且只有一个交点:③当Δ<0时,两个函数图象没有交点.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
