北师大版数学九年级上册:5.1 投影 导学案(含答案)
文档属性
| 名称 | 北师大版数学九年级上册:5.1 投影 导学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 21:38:23 | ||
图片预览



文档简介
11391900118491005.1投影 导学案
第1课时 投影、中心投影
1、预习目标
1.物体在光线的照射下,会在地面和其他平面上留下它的影子,这是投影现象,影子所在的平面称为投影面.
2.灯光的光线可以看成是从一个点发出的,这样的光线所形成的投影称为中心投影.
3.点光源下物体的顶端、影子的顶端(或端点)及点光源在一条直线上,不同物体的顶端及其影子的顶端(或端点)所在的直线都相交于点光源.
2、课堂精讲精练
【例1】 如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)_①_.
①越来越长,②越来越短,③长度不变.
小明在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是_5.95米.
【跟踪训练1】 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向下移时,圆形阴影的大小变化情况是(A)
A.越来越小
B.越来越大
C.大小不变
D.不能确定
【例2】 如图是小明与爸爸(线段AB)、爷爷(线段CD)在同一路灯下的情景,其中,粗线分别表示三人的影子.
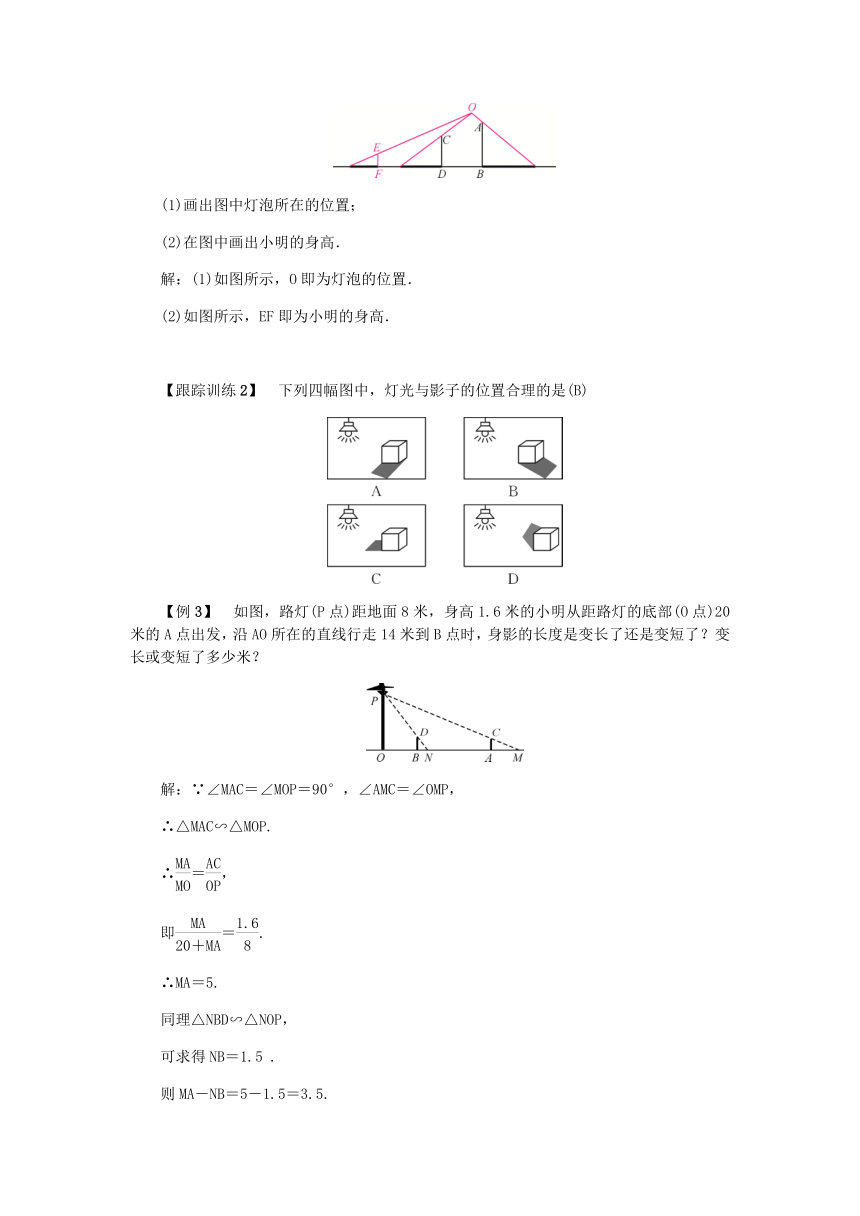
(1)画出图中灯泡所在的位置;
(2)在图中画出小明的身高.
解:(1)如图所示,O即为灯泡的位置.
(2)如图所示,EF即为小明的身高.
【跟踪训练2】 下列四幅图中,灯光与影子的位置合理的是(B)
【例3】 如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点出发,沿AO所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
解:∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
∴△MAC∽△MOP.
∴=,
即=.
∴MA=5.
同理△NBD∽△NOP,
可求得NB=1.5 .
则MA-NB=5-1.5=3.5.
∴小明的身影变短了,短了3.5米.
【跟踪训练3】 小明家的客厅有一张直径为1.2米,高0.8米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立如图的平面直角坐标系,其中D点坐标为(2,0),则点E的坐标是(4,0).
3、课堂巩固训练
1.下列各种现象属于中心投影的是(B)
A.上午人走在路上的影子
B.晚上人走在路灯下的影子
C.中午用来乘凉的树影
D.早上升旗时地面上旗杆的影子
2.如图,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为(B)
A.8 cm B.20 cm C.3.2 cm D.10 cm
3.两根不一样长的木杆垂直竖立在地面上,若它们的影长相等,则此时的投影是中心投影.
4.如图,已知路灯离地面的高度AB为4.8 m,身高为1.6 m的小明站在D处的影长为2 m,那么此时小明离电杆AB的距离BD为4m.
5.小华和小明在同一盏路灯下的影长如图所示,请找出路灯的位置.
解:如图,点P即为路灯灯泡所在位置.
4、课堂总结
1.作一物体中心投影的方法即可以过投影中心与物体的顶端作直线,直线与投影面的交点与物体的底端之间的线段即为该物体的影子.
2.求光源点的方法:
(1)过一物体的顶端及其影子的顶端作一直线;
(2)过另一物体的顶端及其影子的顶端也作一直线,两直线的交点即为光源点.
3.中心投影下物体的影子随光源的位置和方向的变化而变化,同时也随物体的位置和方向的变化而变化.
4.观察物体时,盲区的大小与视点和物体的远近有关,也与视线前是否有障碍物有关.第2课时 平行投影
第2课时 平行投影
1、预习目标
1.太阳光线可以看成平行光线,平行光线所形成的投影称为平行投影.
2.平行光线与投影面垂直时,这种投影称为正投影.
3.将一个圆形纸板放在太阳光下,它所形成的投影可能是圆,也可能是椭圆,还可能是线段.
4.在同一时刻,不同物体在阳光下的影长与物高是成正比例的.
2、课堂精讲精练
【例1】 (1)如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是(B)
A.③-④-①-② B.②-①-④-③
C.④-①-②-③ D.④-①-③-②
(2)如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于10米.
【跟踪训练1】 下面4个图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是④①③②.
【例2】 【注重动手操作】如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6 m的小明(AB)落在地面上的影长为BC=2.4 m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16 m,请求出旗杆DE的高度.
解:(1)影子EG如图所示.
(2)∵DG∥AC,
∴∠ACB=∠DGE.
又∵∠ABC=∠DEG=90°,
∴Rt△ABC∽△Rt△DEG.
∴=,即=.解得DE=.
∴旗杆DE的高度为 m.
【跟踪训练2】 如图是住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=30 m,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高(精确到0.1 m,≈1.73);
(2)若甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
解:(1)延长OB交DC于点E,作EF⊥AB,交AB于F,易得矩形ACEF,∴AF=CE.
在Rt△BEF中,
∵EF=AC=30 m,∠FEB=30°,
∴BE=2BF.
设BF=x,则BE=2x.
根据勾股定理知BE2=BF2+EF2,
∴(2x)2=x2+302,
∴x=10(负值舍去).
∴x≈17.3(m).
∴EC=AF=30-17.3=12.7(m).
(2)当甲幢楼的影子刚好落在点C处时,△ABC为等腰三角形,
因此,当太阳光与水平线夹角为45°时,甲楼的影子刚好不落在乙楼的墙上.
3、课堂巩固训练
1.下列现象不属于投影的是(B)
A.皮影 B.素描画 C.手影 D.树影
2.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是(D)
3.如图所示,甲、乙两建筑物在太阳光的照射下的影子的端点重合在C处,若BC=20 m,CD=40 m,乙的楼高BE=15 m,则甲的楼高AD=30m.
4.如图所示,太阳光线AC和A′C′是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?说明理由.
解:建筑物一样高.
证明:∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°.
∵AC∥A′C′,∴∠ACB=∠A′C′B′.
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
∴AB=A′B′,即建筑物一样高.
4、课堂总结
1.由于平行投影的光线是平行的,而物体的顶端与影子的顶端确定的直线就是光线,故根据另一物体的顶端可作出其影子.
2.在同一时刻,相互平行的物体在太阳光下的投影也是平行的.
3.在同一时刻,相互平行的物体的高与影长成正比,这个性质为我们提供了一种测量较高物体高度的重要方法.
4.在不同时刻,物体在太阳光下形成的影子的长短、方向和形状都是不同的.
5.平行投影与中心投影的区别与联系
区别
联系
光线
物体与投影面
平行时的投影
平行
投影
平行的光线
全等
都是物体在光线的照射下,在某个平面内形成的影子(即都是投影)
中心
投影
从一点出发
的光线
放大(位似变
换)
第1课时 投影、中心投影
1、预习目标
1.物体在光线的照射下,会在地面和其他平面上留下它的影子,这是投影现象,影子所在的平面称为投影面.
2.灯光的光线可以看成是从一个点发出的,这样的光线所形成的投影称为中心投影.
3.点光源下物体的顶端、影子的顶端(或端点)及点光源在一条直线上,不同物体的顶端及其影子的顶端(或端点)所在的直线都相交于点光源.
2、课堂精讲精练
【例1】 如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)_①_.
①越来越长,②越来越短,③长度不变.
小明在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是_5.95米.
【跟踪训练1】 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向下移时,圆形阴影的大小变化情况是(A)
A.越来越小
B.越来越大
C.大小不变
D.不能确定
【例2】 如图是小明与爸爸(线段AB)、爷爷(线段CD)在同一路灯下的情景,其中,粗线分别表示三人的影子.
(1)画出图中灯泡所在的位置;
(2)在图中画出小明的身高.
解:(1)如图所示,O即为灯泡的位置.
(2)如图所示,EF即为小明的身高.
【跟踪训练2】 下列四幅图中,灯光与影子的位置合理的是(B)
【例3】 如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点出发,沿AO所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
解:∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
∴△MAC∽△MOP.
∴=,
即=.
∴MA=5.
同理△NBD∽△NOP,
可求得NB=1.5 .
则MA-NB=5-1.5=3.5.
∴小明的身影变短了,短了3.5米.
【跟踪训练3】 小明家的客厅有一张直径为1.2米,高0.8米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立如图的平面直角坐标系,其中D点坐标为(2,0),则点E的坐标是(4,0).
3、课堂巩固训练
1.下列各种现象属于中心投影的是(B)
A.上午人走在路上的影子
B.晚上人走在路灯下的影子
C.中午用来乘凉的树影
D.早上升旗时地面上旗杆的影子
2.如图,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为(B)
A.8 cm B.20 cm C.3.2 cm D.10 cm
3.两根不一样长的木杆垂直竖立在地面上,若它们的影长相等,则此时的投影是中心投影.
4.如图,已知路灯离地面的高度AB为4.8 m,身高为1.6 m的小明站在D处的影长为2 m,那么此时小明离电杆AB的距离BD为4m.
5.小华和小明在同一盏路灯下的影长如图所示,请找出路灯的位置.
解:如图,点P即为路灯灯泡所在位置.
4、课堂总结
1.作一物体中心投影的方法即可以过投影中心与物体的顶端作直线,直线与投影面的交点与物体的底端之间的线段即为该物体的影子.
2.求光源点的方法:
(1)过一物体的顶端及其影子的顶端作一直线;
(2)过另一物体的顶端及其影子的顶端也作一直线,两直线的交点即为光源点.
3.中心投影下物体的影子随光源的位置和方向的变化而变化,同时也随物体的位置和方向的变化而变化.
4.观察物体时,盲区的大小与视点和物体的远近有关,也与视线前是否有障碍物有关.第2课时 平行投影
第2课时 平行投影
1、预习目标
1.太阳光线可以看成平行光线,平行光线所形成的投影称为平行投影.
2.平行光线与投影面垂直时,这种投影称为正投影.
3.将一个圆形纸板放在太阳光下,它所形成的投影可能是圆,也可能是椭圆,还可能是线段.
4.在同一时刻,不同物体在阳光下的影长与物高是成正比例的.
2、课堂精讲精练
【例1】 (1)如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是(B)
A.③-④-①-② B.②-①-④-③
C.④-①-②-③ D.④-①-③-②
(2)如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于10米.
【跟踪训练1】 下面4个图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是④①③②.
【例2】 【注重动手操作】如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6 m的小明(AB)落在地面上的影长为BC=2.4 m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16 m,请求出旗杆DE的高度.
解:(1)影子EG如图所示.
(2)∵DG∥AC,
∴∠ACB=∠DGE.
又∵∠ABC=∠DEG=90°,
∴Rt△ABC∽△Rt△DEG.
∴=,即=.解得DE=.
∴旗杆DE的高度为 m.
【跟踪训练2】 如图是住宅区内的两幢楼,它们的高AB=CD=30 m,两楼间的距离AC=30 m,现需了解甲楼对乙楼的采光的影响情况.
(1)当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高(精确到0.1 m,≈1.73);
(2)若甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
解:(1)延长OB交DC于点E,作EF⊥AB,交AB于F,易得矩形ACEF,∴AF=CE.
在Rt△BEF中,
∵EF=AC=30 m,∠FEB=30°,
∴BE=2BF.
设BF=x,则BE=2x.
根据勾股定理知BE2=BF2+EF2,
∴(2x)2=x2+302,
∴x=10(负值舍去).
∴x≈17.3(m).
∴EC=AF=30-17.3=12.7(m).
(2)当甲幢楼的影子刚好落在点C处时,△ABC为等腰三角形,
因此,当太阳光与水平线夹角为45°时,甲楼的影子刚好不落在乙楼的墙上.
3、课堂巩固训练
1.下列现象不属于投影的是(B)
A.皮影 B.素描画 C.手影 D.树影
2.李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是(D)
3.如图所示,甲、乙两建筑物在太阳光的照射下的影子的端点重合在C处,若BC=20 m,CD=40 m,乙的楼高BE=15 m,则甲的楼高AD=30m.
4.如图所示,太阳光线AC和A′C′是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?说明理由.
解:建筑物一样高.
证明:∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°.
∵AC∥A′C′,∴∠ACB=∠A′C′B′.
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
∴AB=A′B′,即建筑物一样高.
4、课堂总结
1.由于平行投影的光线是平行的,而物体的顶端与影子的顶端确定的直线就是光线,故根据另一物体的顶端可作出其影子.
2.在同一时刻,相互平行的物体在太阳光下的投影也是平行的.
3.在同一时刻,相互平行的物体的高与影长成正比,这个性质为我们提供了一种测量较高物体高度的重要方法.
4.在不同时刻,物体在太阳光下形成的影子的长短、方向和形状都是不同的.
5.平行投影与中心投影的区别与联系
区别
联系
光线
物体与投影面
平行时的投影
平行
投影
平行的光线
全等
都是物体在光线的照射下,在某个平面内形成的影子(即都是投影)
中心
投影
从一点出发
的光线
放大(位似变
换)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
