一次函数图象的应用（2）

课题： 6.5 一次函数图象的应用（2） 主备人：左良成
学习目标
一、进一步训练学生的识图能力，能通过函数图象获取信息，解决简单的实际问题；
二、能利用二个一次函数图象解决较复杂的实际问题；
学习重点：利用函数图象解决各种生活问题。
学习难点：正确地根据图象获取信息，并解决现实生活中的有关问题．
知识回顾
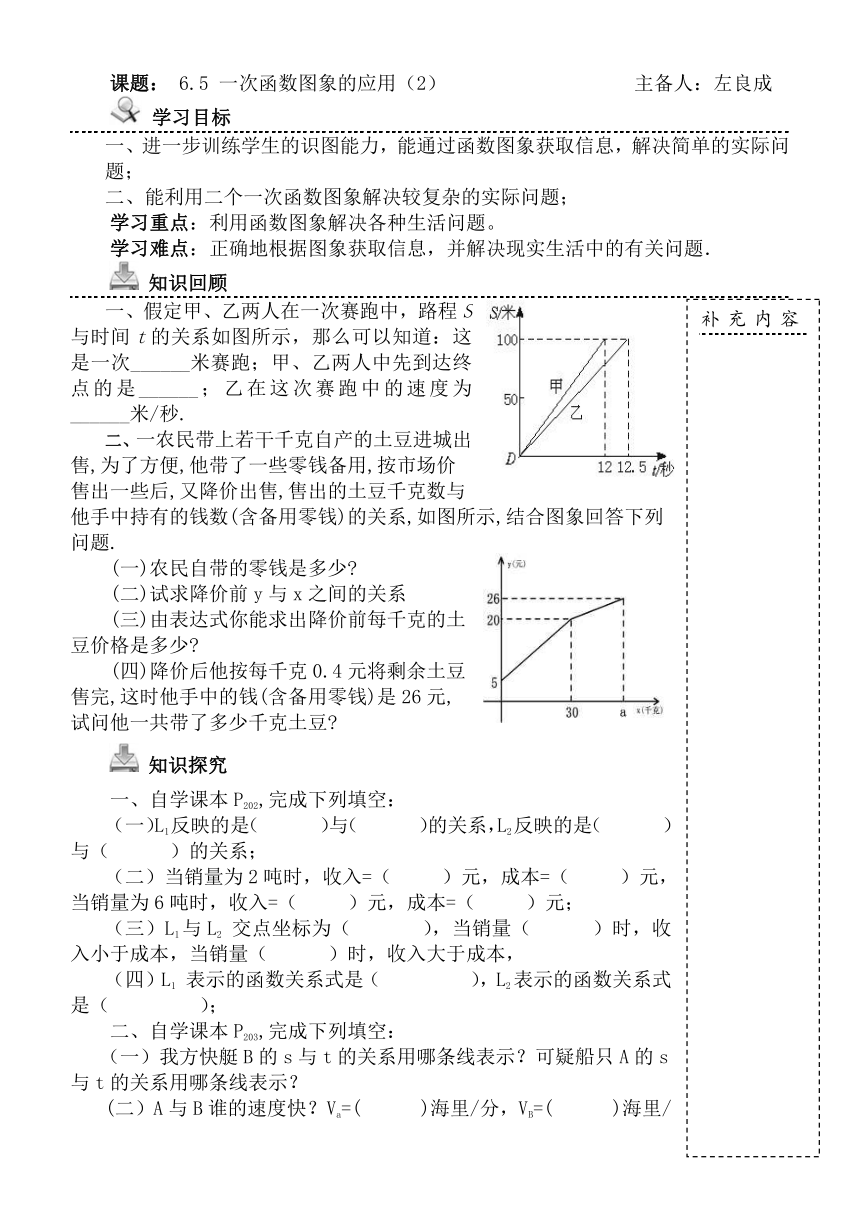
一、假定甲、乙两人在一次赛跑中，路程S与时间t的关系如图所示，那么可以知道：这是一次______米赛跑；甲、乙两人中先到达终点的是______；乙在这次赛跑中的速度为______米/秒.
二、一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(一)农民自带的零钱是多少
(二)试求降价前y与x之间的关系
(三)由表达式你能求出降价前每千克的土豆价格是多少
(四)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆
知识探究
一、自学课本P202,完成下列填空：
（一）L1反映的是（ ）与（ ）的关系，L2反映的是（ ）与（ ）的关系；
（二）当销量为2吨时，收入=（ ）元，成本=（ ）元，当销量为6吨时，收入=（ ）元，成本=（ ）元；
（三）L1与L2 交点坐标为（ ），当销量（ ）时，收入小于成本，当销量（ ）时，收入大于成本，
（四）L1 表示的函数关系式是（ ），L2表示的函数关系式是（ ）；
二、自学课本P203,完成下列填空：
（一）我方快艇B的s与t的关系用哪条线表示？可疑船只A的s与t的关系用哪条线表示？
(二）A与B谁的速度快？Va=( )海里/分，VB=( )海里/分；
（三）延长L1与L2，观察图象，15分钟内B能否追上A？
（四）一直追下去，B能否追上A？为什么？
（五）观察图象，在离海岸12海里内，B能否将A拦截？
知识反馈
基础题：
如图1：OA、BA分别表示甲乙两名学生运动的一次函数的图象，图中s和t分别表示运动的路程和时间，根据图象请你判断：
（1）甲乙谁的速度比较快？为什么？
答：___________________________________________.
（2）快者的速度比慢者的速度每秒快多少米？
答：____________________________________________.
提高题：
某移动通讯公司开设两种业务.“全球通”：先缴50元月租费，然后每通话1分钟，再付0.4元，“神州行”：不缴纳月租费，每通话1分钟，付话费0.6元（通话均指市话）.若设一个月内通话x分钟，两种方式的费用分别为y1和y2元.（通话时不足1分钟的按1分钟计算，如3分20秒按4分钟收费）
（1）写出y1、y2与x之间的函数关系式.
（2）在同一坐标系下做出以上两个函数的图象.
（3）一个月内通话多少分钟，两种费用相同.
（4）某人估计一个月内通话300分钟，应选择哪种合算？
创新题：
一家小型放影厅盈利额y（元）同售票数x之间的关系如图2所示，其中保险部门规定：超过150人时，要缴纳公安消防保险费50元.试根据关系图回答下列问题：
（1）当售票数x满足0＜x≤150时，盈利额y（元）与x之间的函数关系式是________.
（2）当售票数x满足150＜x≤250时，盈利额y（元）与x之间的函数关系式是________.
（3）当售票数x为__________时，不赔不赚；当售票数x满足__________时，放影厅要赔本；若放影厅要获得最大利润200元，此时售票数x应为________.
（4）当x满足________时，此时利润比x=150时多.
知识小结
应用多个一次函数图象解决实际问题时需注意什么？
课后反思
补充内容