2020-2021学年华东师大新版九年级上册数学《第23章 图形的相似》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版九年级上册数学《第23章 图形的相似》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
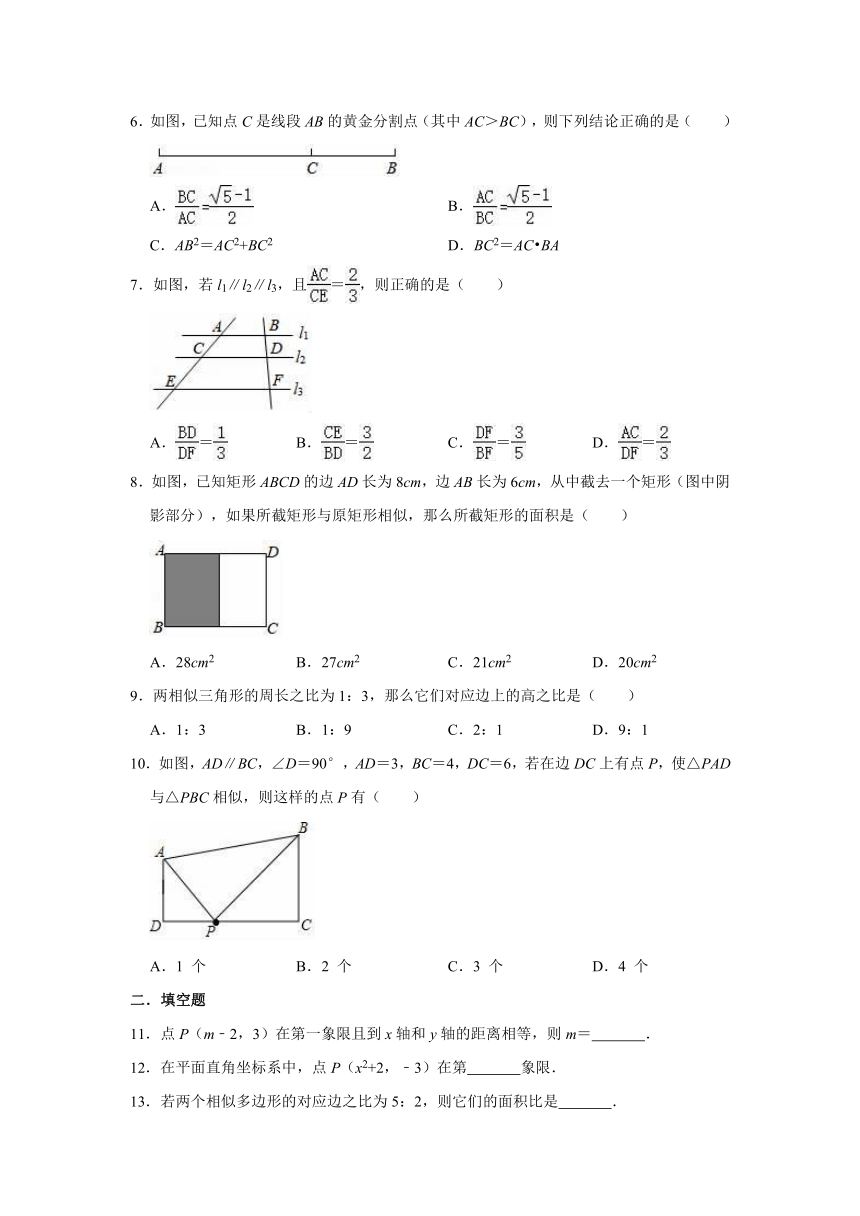
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 00:00:00 | ||
图片预览


文档简介
2020-2021学年华东师大新版九年级上册数学《第23章
图形的相似》单元测试卷
一.选择题
1.在平面直角坐标系xOy中,点P的坐标是(m2+1,﹣2020),则点P的位置在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知,则下列式子不一定成立的是( )
A.
B.
C.
D.3y﹣5=5(x﹣1)
3.若某个直角三角形的两直角边之比为2:3,则确定了该三角形的( )
A.形状
B.周长
C.面积
D.斜边
4.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12.若D,E分别为边AC,BC的中点,则DE的长为( )
A.5
B.5.5
C.6
D.6.5
5.如图,以点O为位似中心,画一个四边形A'B'C'D',使它与四边形ABCD位似,且相似比为,则下列说法错误的是( )
A.四边形ABCD∽四边形A'B'C'D'
B.点C,O,C′三点在同一直线上
C.=
D.OB=OB′
6.如图,已知点C是线段AB的黄金分割点(其中AC>BC),则下列结论正确的是( )
A.
B.
C.AB2=AC2+BC2
D.BC2=AC?BA
7.如图,若l1∥l2∥l3,且=,则正确的是( )
A.=
B.=
C.=
D.=
8.如图,已知矩形ABCD的边AD长为8cm,边AB长为6cm,从中截去一个矩形(图中阴影部分),如果所截矩形与原矩形相似,那么所截矩形的面积是( )
A.28cm2
B.27cm2
C.21cm2
D.20cm2
9.两相似三角形的周长之比为1:3,那么它们对应边上的高之比是( )
A.1:3
B.1:9
C.2:1
D.9:1
10.如图,AD∥BC,∠D=90°,AD=3,BC=4,DC=6,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有( )
A.1
个
B.2
个
C.3
个
D.4
个
二.填空题
11.点P(m﹣2,3)在第一象限且到x轴和y轴的距离相等,则m=
.
12.在平面直角坐标系中,点P(x2+2,﹣3)在第
象限.
13.若两个相似多边形的对应边之比为5:2,则它们的面积比是
.
14.△ABC中,各边中点围成的三角形周长是3cm,则△ABC的周长为
.
15.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2cm,则它的最长边为
cm.
16.已知一个梯形的中位线长为5cm,其中一条底边的长为6cm,那么该梯形的另一条底边的长是
cm.
17.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AC=8,AE=6,AB=12,则BD等于
.
18.将一根2m的绳子黄金分割,分割后较长绳子的长约是
m(精确到0.01m).
19.如图,四边形ABCD与四边形EFGH是位似图形,位似中心是点O,已知,则=
.
20.如图,四边形EFGH是△ABC内接正方形,BC=20cm,高AD=12cm,则内接正方形的边长EF=
cm.
三.解答题
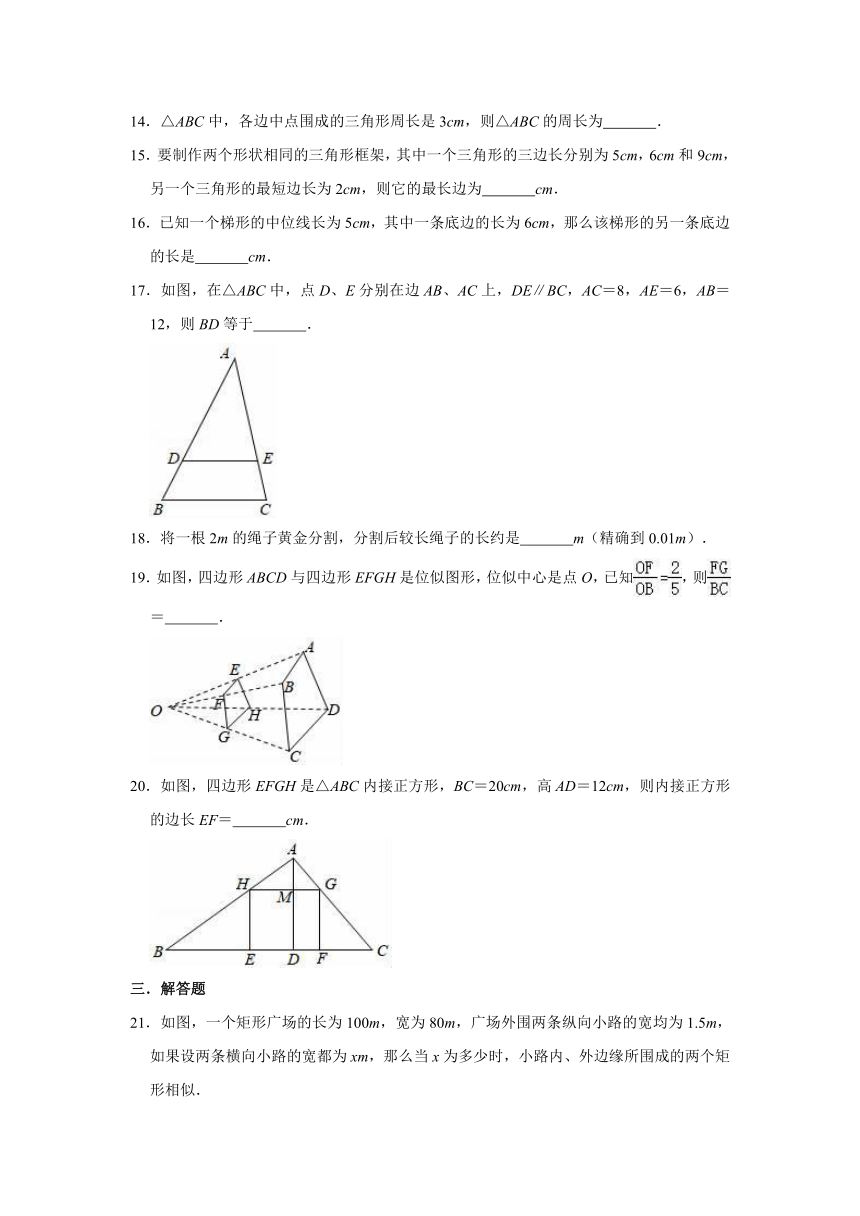
21.如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果设两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.
22.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=20°,求∠PFE的度数.
23.三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图,△ABC中,AB=AC,且∠A=36°.
(1)在图中用尺规作边AB的垂直平分线交AC于D,交AB于E,连接BD(保留作图痕迹);
(2)请问△BDC是不是黄金三角形,如果是,请给出证明,如果不是,请说明理由.
24.如图,DE∥AB,EF∥BC,AF=5cm,FB=3cm,CD=2cm,求BD的长.
25.在平面直角坐标系中,已知点M的坐标为(2m+3,m﹣1).
(1)若点M在x轴上,求m的值;
(2)已知点N的坐标为(﹣3,2),且直线MN⊥x轴,求线段MN的长.
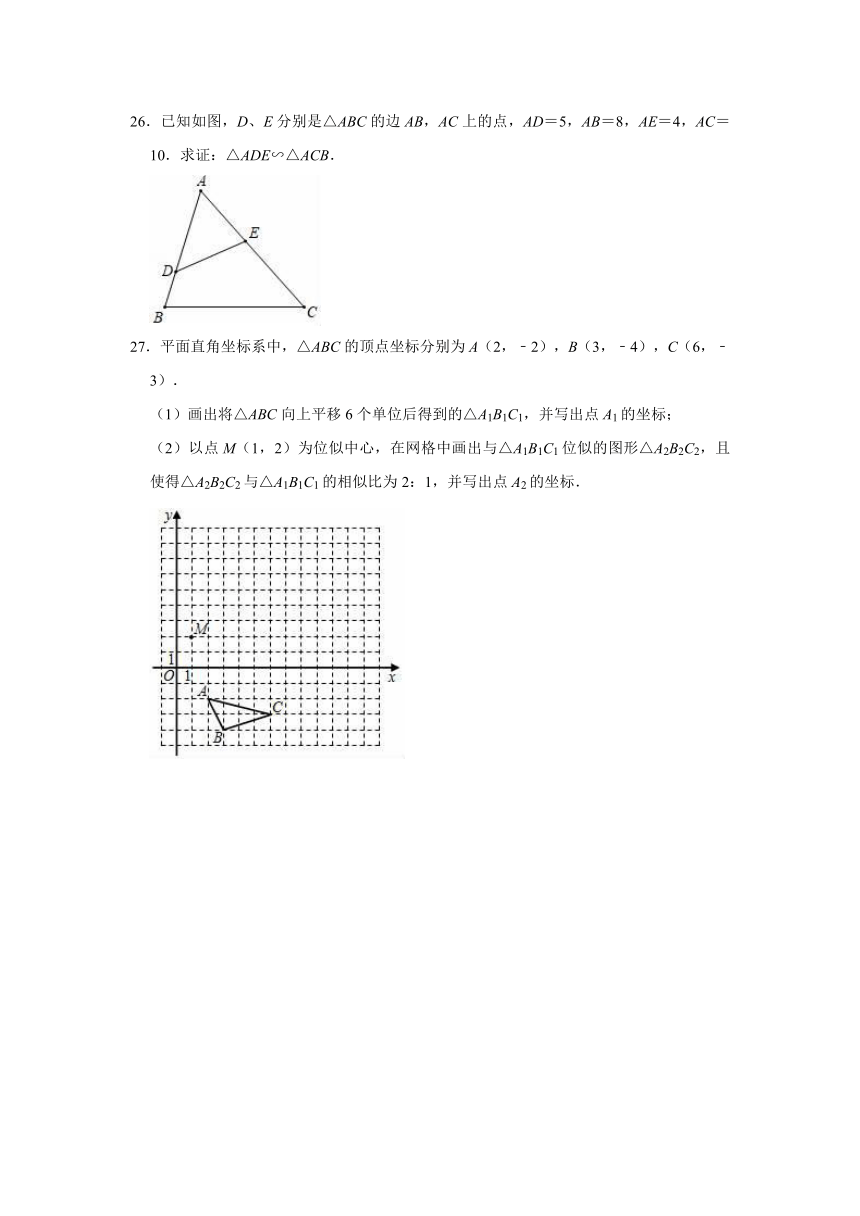
26.已知如图,D、E分别是△ABC的边AB,AC上的点,AD=5,AB=8,AE=4,AC=10.求证:△ADE∽△ACB.
27.平面直角坐标系中,△ABC的顶点坐标分别为A(2,﹣2),B(3,﹣4),C(6,﹣3).
(1)画出将△ABC向上平移6个单位后得到的△A1B1C1,并写出点A1的坐标;
(2)以点M(1,2)为位似中心,在网格中画出与△A1B1C1位似的图形△A2B2C2,且使得△A2B2C2与△A1B1C1的相似比为2:1,并写出点A2的坐标.
参考答案与试题解析
一.选择题
1.解:∵m2≥0,
∴m2+1>0,
∴点P(m2+1,﹣2020)的位置在第四象限.
故选:D.
2.解:∵,
∴==,
故A成立;
当x=3,y=5时,
则,
==,
∴≠,
故B不一定成立;
∵,
∴==﹣,
故C
成立;
∵,
∴3y=5x,
∴3y﹣5=5x﹣5,
∴3y﹣5=5(x﹣1),
故D成立;
故选:B.
3.解:∵直角三角形的两直角边之比为2:3,
∴虽不能确定两直角边的值,但能确定其比值,
∴能确定该直角三角形的形状,
故选:A.
4.解:∵∠C=90°,AC=5,BC=12,
∴AB===13,
∵AD=DC,CE=EB,
∴DE=AB=6.5,
故选:D.
5.解:∵四边形A'B'C'D'与四边形ABCD位似,
∴四边形A'B'C'D'∽四边形ABCD,A选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,
∴点C,O,C′三点在同一直线上,B选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,位似比为,
∴=,C选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,位似比为,
∴AB∥A′B′,
∴==,
∴OB=OB′,D选项说法错误,符合题意;
故选:D.
6.解:∵点C是线段AB的黄金分割点,且AC>BC,
∴==,
∴选项A符合题意,
AC2=BC?AB,
∴选项D不符合题意;
∵==,
∴选项B不符合题意;
∵AB2≠AC2+BC2,
∴选项C不符合题意;
故选:A.
7.解:∵l1∥l2∥l3,且=,
∴=,
∴=;
故选:C.
8.解:依题意,在矩形ABDC中截取矩形ABFE,
则矩形ABDC∽矩形AEFB,
则,
设AE=x(cm),得到:
,
解得:x=4.5,
则截取的矩形面积是:6×4.5=27(cm2).
故选:B.
9.解:∵两相似三角形的周长之比为1:3,
∴两相似三角形的相似比为1:3,
∴它们对应边上的高之比等于相似比=1:3,
故选:A.
10.解:∵AB⊥BC,
∴∠B=90°.
∵AD∥BC
∴∠A=180°﹣∠B=90°,
∴∠PAD=∠PBC=90°.
设DP的长为x,则CP长为6﹣x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则DP:CP=AD:BC,
即x:(6﹣x)=3:4,
解得:x=
②若△APD∽△BPC,则DP:PC=AD:BC,
即x:4=3:(6﹣x),
整理得:x2﹣6x+12=0,
∵△<0,
这种情形不存在,
∴满足条件的点P的个数是1个,
故选:A.
二.填空题
11.解:∵点P(m﹣2,3)在第一象限且到x轴和y轴的距离相等,
∴m﹣2=3,
解得:m=5.
故答案为:5.
12.解:∵x2≥0,
∴x2+2>0,
∴点P(x2+2,﹣3)的位置在第四象限.
故答案为:四.
13.解:∵两个相似多边形的对应边的比是5:2,
∴这两个多边形的面积比是52:22,
即这两个多边形的面积比是25:4,
故答案为:25:4.
14.解:∵D、E、F分别为AB、AC、BC的中点,
∴AB=2EF,AC=2DF,BC=2DE,
∵△DEF的周长为3,
∴DE+DF+EF=3,
∴△ABC的周长=AB+AC+BC=2(DE+DF+EF)=6(cm),
故答案为:6cm.
15.解:设另一个三角形的最长边为xcm,
∵两个三角形相似,
∴=,
解得,x=,
则另一个三角形的最长边为cm,
故答案为:.
16.解:设梯形的另一条底边为xcm,
由题意得:6+x=2×5,
解得x=4.
即梯形的另一条底边的长为4cm.
故答案为:4.
17.解:∵DE∥BC,
∴=,
∵AC=8,AE=6,AB=12,
∴=,
∴AD=9,
∴BD=AB﹣AD=12﹣9=3.
故答案为:3.
18.解:分割后较长绳子的长约为:(m),
故答案为:1.24.
19.解:∵四边形ABCD与四边形EFGH是位似图形,
∴FG∥BC,
∴△OFG∽△OBC,
∴,
∵,
∴=,
故答案为:.
20.解:设EF=xcm,则HG=MD=xcm,
∵四边形EFGH是△ABC内接正方形,
∴HG∥BC,
∴△AHG∽△ABC,
∴,
∵BC=20cm,高AD=12cm,
∴AM=(12﹣x)cm,
∴,
解得x=7.5,
即EF的长为7.5cm,
故答案为:7.5.
三.解答题
21.解:当(100+3):100=(80+2x):80时,小路内、外边缘所围成的两个矩形相似.
解得x=1.2
答:当x为1.2m时,小路内、外边缘所围成的两个矩形相似.
22.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=20°.
23.解:(1)作边AB的垂直平分线交AC于D,交AB于E,连接BD,如图所示:
(2)△BDC是黄金三角形,理由如下:
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=36°,
∵∠A=36°,AB=AC,
∴∠ABC=∠C=(180°﹣36°)=72°,
∴∠DBC=∠ABC﹣∠ABD=72°﹣36°=36°,
又∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴△BDC是黄金三角形.
24.解:∵DE∥AB,EF∥BC,AF=5cm,FB=3cm,CD=2cm,
∴,
∴=,
∴,
解得:BD=cm.
25.解:(1)由题意得:m﹣1=0,
解得:m=1;
(2)∵点N(﹣3,2),且直线MN⊥x轴,
∴m﹣1=﹣3,
解得
m=﹣2.
∴M(﹣3,﹣3),
∴MN=2﹣(﹣3)=5.
26.证明:∵AD=5,AB=8,AE=4,AC=10,
∴,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB.
27.解:(1)如图,△A1B1C1为所作,A1(2,4);
(2)如图,△A2B2C2为所作,A2(3,6).
图形的相似》单元测试卷
一.选择题
1.在平面直角坐标系xOy中,点P的坐标是(m2+1,﹣2020),则点P的位置在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知,则下列式子不一定成立的是( )
A.
B.
C.
D.3y﹣5=5(x﹣1)
3.若某个直角三角形的两直角边之比为2:3,则确定了该三角形的( )
A.形状
B.周长
C.面积
D.斜边
4.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12.若D,E分别为边AC,BC的中点,则DE的长为( )
A.5
B.5.5
C.6
D.6.5
5.如图,以点O为位似中心,画一个四边形A'B'C'D',使它与四边形ABCD位似,且相似比为,则下列说法错误的是( )
A.四边形ABCD∽四边形A'B'C'D'
B.点C,O,C′三点在同一直线上
C.=
D.OB=OB′
6.如图,已知点C是线段AB的黄金分割点(其中AC>BC),则下列结论正确的是( )
A.
B.
C.AB2=AC2+BC2
D.BC2=AC?BA
7.如图,若l1∥l2∥l3,且=,则正确的是( )
A.=
B.=
C.=
D.=
8.如图,已知矩形ABCD的边AD长为8cm,边AB长为6cm,从中截去一个矩形(图中阴影部分),如果所截矩形与原矩形相似,那么所截矩形的面积是( )
A.28cm2
B.27cm2
C.21cm2
D.20cm2
9.两相似三角形的周长之比为1:3,那么它们对应边上的高之比是( )
A.1:3
B.1:9
C.2:1
D.9:1
10.如图,AD∥BC,∠D=90°,AD=3,BC=4,DC=6,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有( )
A.1
个
B.2
个
C.3
个
D.4
个
二.填空题
11.点P(m﹣2,3)在第一象限且到x轴和y轴的距离相等,则m=
.
12.在平面直角坐标系中,点P(x2+2,﹣3)在第
象限.
13.若两个相似多边形的对应边之比为5:2,则它们的面积比是
.
14.△ABC中,各边中点围成的三角形周长是3cm,则△ABC的周长为
.
15.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2cm,则它的最长边为
cm.
16.已知一个梯形的中位线长为5cm,其中一条底边的长为6cm,那么该梯形的另一条底边的长是
cm.
17.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AC=8,AE=6,AB=12,则BD等于
.
18.将一根2m的绳子黄金分割,分割后较长绳子的长约是
m(精确到0.01m).
19.如图,四边形ABCD与四边形EFGH是位似图形,位似中心是点O,已知,则=
.
20.如图,四边形EFGH是△ABC内接正方形,BC=20cm,高AD=12cm,则内接正方形的边长EF=
cm.
三.解答题
21.如图,一个矩形广场的长为100m,宽为80m,广场外围两条纵向小路的宽均为1.5m,如果设两条横向小路的宽都为xm,那么当x为多少时,小路内、外边缘所围成的两个矩形相似.
22.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=20°,求∠PFE的度数.
23.三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图,△ABC中,AB=AC,且∠A=36°.
(1)在图中用尺规作边AB的垂直平分线交AC于D,交AB于E,连接BD(保留作图痕迹);
(2)请问△BDC是不是黄金三角形,如果是,请给出证明,如果不是,请说明理由.
24.如图,DE∥AB,EF∥BC,AF=5cm,FB=3cm,CD=2cm,求BD的长.
25.在平面直角坐标系中,已知点M的坐标为(2m+3,m﹣1).
(1)若点M在x轴上,求m的值;
(2)已知点N的坐标为(﹣3,2),且直线MN⊥x轴,求线段MN的长.
26.已知如图,D、E分别是△ABC的边AB,AC上的点,AD=5,AB=8,AE=4,AC=10.求证:△ADE∽△ACB.
27.平面直角坐标系中,△ABC的顶点坐标分别为A(2,﹣2),B(3,﹣4),C(6,﹣3).
(1)画出将△ABC向上平移6个单位后得到的△A1B1C1,并写出点A1的坐标;
(2)以点M(1,2)为位似中心,在网格中画出与△A1B1C1位似的图形△A2B2C2,且使得△A2B2C2与△A1B1C1的相似比为2:1,并写出点A2的坐标.
参考答案与试题解析
一.选择题
1.解:∵m2≥0,
∴m2+1>0,
∴点P(m2+1,﹣2020)的位置在第四象限.
故选:D.
2.解:∵,
∴==,
故A成立;
当x=3,y=5时,
则,
==,
∴≠,
故B不一定成立;
∵,
∴==﹣,
故C
成立;
∵,
∴3y=5x,
∴3y﹣5=5x﹣5,
∴3y﹣5=5(x﹣1),
故D成立;
故选:B.
3.解:∵直角三角形的两直角边之比为2:3,
∴虽不能确定两直角边的值,但能确定其比值,
∴能确定该直角三角形的形状,
故选:A.
4.解:∵∠C=90°,AC=5,BC=12,
∴AB===13,
∵AD=DC,CE=EB,
∴DE=AB=6.5,
故选:D.
5.解:∵四边形A'B'C'D'与四边形ABCD位似,
∴四边形A'B'C'D'∽四边形ABCD,A选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,
∴点C,O,C′三点在同一直线上,B选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,位似比为,
∴=,C选项说法正确,不符合题意;
∵四边形A'B'C'D'与四边形ABCD位似,位似比为,
∴AB∥A′B′,
∴==,
∴OB=OB′,D选项说法错误,符合题意;
故选:D.
6.解:∵点C是线段AB的黄金分割点,且AC>BC,
∴==,
∴选项A符合题意,
AC2=BC?AB,
∴选项D不符合题意;
∵==,
∴选项B不符合题意;
∵AB2≠AC2+BC2,
∴选项C不符合题意;
故选:A.
7.解:∵l1∥l2∥l3,且=,
∴=,
∴=;
故选:C.
8.解:依题意,在矩形ABDC中截取矩形ABFE,
则矩形ABDC∽矩形AEFB,
则,
设AE=x(cm),得到:
,
解得:x=4.5,
则截取的矩形面积是:6×4.5=27(cm2).
故选:B.
9.解:∵两相似三角形的周长之比为1:3,
∴两相似三角形的相似比为1:3,
∴它们对应边上的高之比等于相似比=1:3,
故选:A.
10.解:∵AB⊥BC,
∴∠B=90°.
∵AD∥BC
∴∠A=180°﹣∠B=90°,
∴∠PAD=∠PBC=90°.
设DP的长为x,则CP长为6﹣x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则DP:CP=AD:BC,
即x:(6﹣x)=3:4,
解得:x=
②若△APD∽△BPC,则DP:PC=AD:BC,
即x:4=3:(6﹣x),
整理得:x2﹣6x+12=0,
∵△<0,
这种情形不存在,
∴满足条件的点P的个数是1个,
故选:A.
二.填空题
11.解:∵点P(m﹣2,3)在第一象限且到x轴和y轴的距离相等,
∴m﹣2=3,
解得:m=5.
故答案为:5.
12.解:∵x2≥0,
∴x2+2>0,
∴点P(x2+2,﹣3)的位置在第四象限.
故答案为:四.
13.解:∵两个相似多边形的对应边的比是5:2,
∴这两个多边形的面积比是52:22,
即这两个多边形的面积比是25:4,
故答案为:25:4.
14.解:∵D、E、F分别为AB、AC、BC的中点,
∴AB=2EF,AC=2DF,BC=2DE,
∵△DEF的周长为3,
∴DE+DF+EF=3,
∴△ABC的周长=AB+AC+BC=2(DE+DF+EF)=6(cm),
故答案为:6cm.
15.解:设另一个三角形的最长边为xcm,
∵两个三角形相似,
∴=,
解得,x=,
则另一个三角形的最长边为cm,
故答案为:.
16.解:设梯形的另一条底边为xcm,
由题意得:6+x=2×5,
解得x=4.
即梯形的另一条底边的长为4cm.
故答案为:4.
17.解:∵DE∥BC,
∴=,
∵AC=8,AE=6,AB=12,
∴=,
∴AD=9,
∴BD=AB﹣AD=12﹣9=3.
故答案为:3.
18.解:分割后较长绳子的长约为:(m),
故答案为:1.24.
19.解:∵四边形ABCD与四边形EFGH是位似图形,
∴FG∥BC,
∴△OFG∽△OBC,
∴,
∵,
∴=,
故答案为:.
20.解:设EF=xcm,则HG=MD=xcm,
∵四边形EFGH是△ABC内接正方形,
∴HG∥BC,
∴△AHG∽△ABC,
∴,
∵BC=20cm,高AD=12cm,
∴AM=(12﹣x)cm,
∴,
解得x=7.5,
即EF的长为7.5cm,
故答案为:7.5.
三.解答题
21.解:当(100+3):100=(80+2x):80时,小路内、外边缘所围成的两个矩形相似.
解得x=1.2
答:当x为1.2m时,小路内、外边缘所围成的两个矩形相似.
22.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=20°.
23.解:(1)作边AB的垂直平分线交AC于D,交AB于E,连接BD,如图所示:
(2)△BDC是黄金三角形,理由如下:
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=36°,
∵∠A=36°,AB=AC,
∴∠ABC=∠C=(180°﹣36°)=72°,
∴∠DBC=∠ABC﹣∠ABD=72°﹣36°=36°,
又∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴△BDC是黄金三角形.
24.解:∵DE∥AB,EF∥BC,AF=5cm,FB=3cm,CD=2cm,
∴,
∴=,
∴,
解得:BD=cm.
25.解:(1)由题意得:m﹣1=0,
解得:m=1;
(2)∵点N(﹣3,2),且直线MN⊥x轴,
∴m﹣1=﹣3,
解得
m=﹣2.
∴M(﹣3,﹣3),
∴MN=2﹣(﹣3)=5.
26.证明:∵AD=5,AB=8,AE=4,AC=10,
∴,
又∵∠DAE=∠CAB,
∴△ADE∽△ACB.
27.解:(1)如图,△A1B1C1为所作,A1(2,4);
(2)如图,△A2B2C2为所作,A2(3,6).
