2020-2021学年华东师大新版九年级上册数学《第24章 解直角三角形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版九年级上册数学《第24章 解直角三角形》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 366.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 19:31:06 | ||
图片预览




文档简介
2020-2021学年华东师大新版九年级上册数学《第24章
解直角三角形》单元测试卷
一.选择题
1.如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB于D,则下列结论错误的是( )
A.CD?AC=AB?BC
B.AC2=AD?AB
C.BC2=BD?AB
D.AC?BC=AB?CD
2.如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinB等于( )
A.
B.
C.
D.
3.已知△ABC是锐角三角形,若AB>AC,则( )
A.sinA<sinB
B.sinB<sinC
C.sinA<sinC
D.sinC<sinA
4.在Rt△ABC中,∠C=90°,若cosB=,则tanA的值是( )
A.
B.
C.
D.
5.如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道,用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是( )
A.
B.
C.
D.
6.已知直角三角形一个锐角的度数为40°,则它的另一个内角(锐角)的度数为( )
A.140°
B.60°
C.50°
D.40°
7.如图,已知∠AOB=60°,P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=5,则ON的长度是( )
A.9
B.6.5
C.6
D.5.5
8.如图,某商场一楼与二楼之间的电梯示意图.∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.
m
B.4m
C.4m
D.8m
9.如图,边长为4的等边△ABC中,CD⊥AB于点D,E为AC中点,则DE的长是( )
A.1
B.2
C.
D.2.5
10.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么cos∠ACB值为( )
A.
B.
C.
D.
二.填空题
11.如果∠α是锐角,且sin,那么tanα的值是
.
12.如图,Rt△ABC中,∠C=90°,AC=4,BC=6,则sinA=
.
13.如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为
海里.
14.用科学计算器计算
sin37.5°(比较大小)
15.已知α为锐角,且满足sin(α+15°)=,则tanα=
.
16.如图,将一个装有水的杯子斜放在水平的桌面上,其截面可看作一个宽BC=6厘米的矩形.当水面触到杯口边缘时,水面宽度BE=12厘米,此时杯子的倾斜角α等于
度.
17.已知等腰三角形的两边长分别为6cm和3cm,则此它周长是
cm;已知等腰三角形的一个内角为50°,则它的顶角为
°.
18.如图,在△ABC中,CD⊥AB交AB于点D,BE⊥AC交AC于点E,F为BC的中点,BC=10,DE=8,则△DEF的面积为
.
19.如图,△ABC中,∠B=70°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为
.
20.在△ABC中,∠ABC=90°,BD⊥AC.若AD=2cm,DC=4cm,则BD=
.
三.解答题
21.已知∠A为锐角且sinA=,则4sin2A﹣4sinAcosA+cos2A的值是多少.
22.选做题(从下面两题中任选一题,如果做了两题的,只按第(2)题评分)
(1)用科学计算器计算:135×sin13°≈
(结果精确到0.1)
(2)已知α是锐角,且sin(α+15°)=.计算﹣4cosα﹣(π﹣3.14)0+tanα+()﹣1的值
23.如图,已知△ABC,∠ACB=90°.
(1)求作AB边上的高CD.(尺规作图,保留作图痕迹,不写作法)
(2)若AD=2,BD=4,求高CD的长.
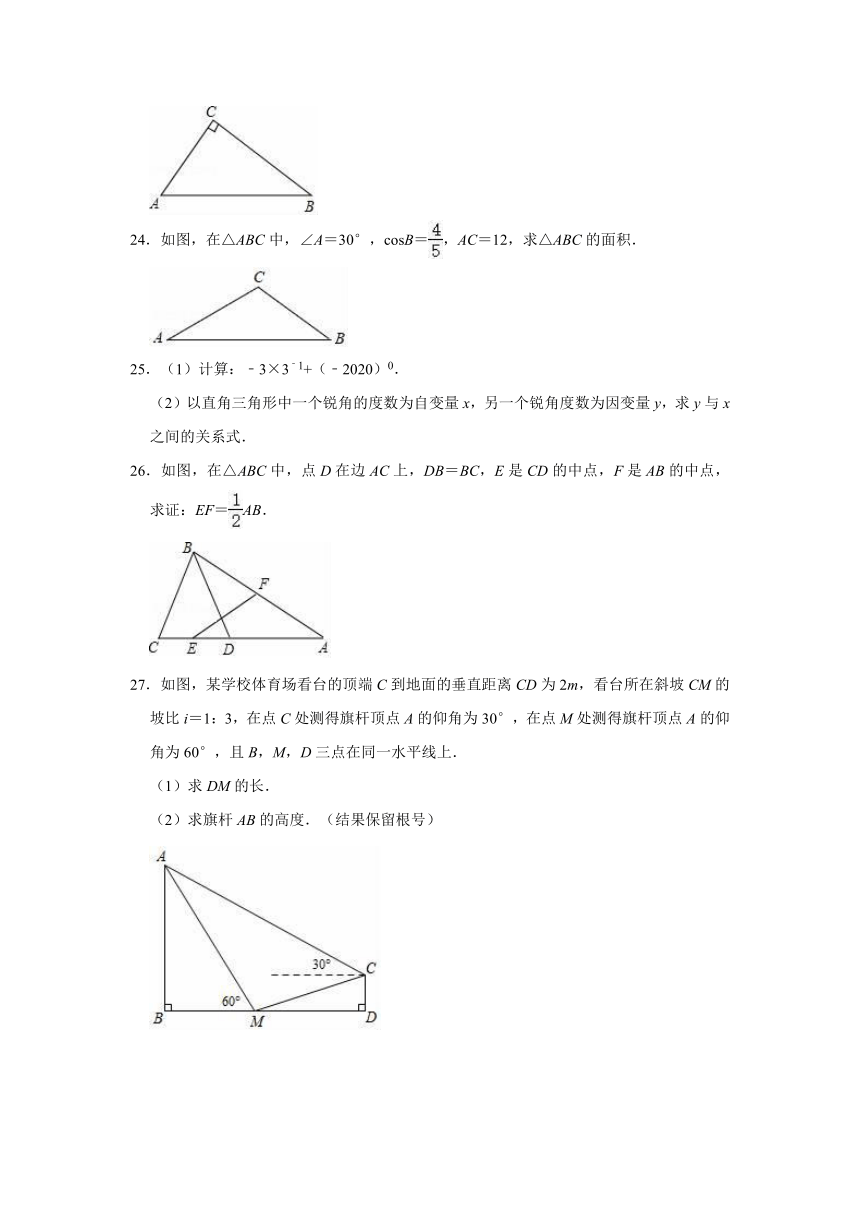
24.如图,在△ABC中,∠A=30°,cosB=,AC=12,求△ABC的面积.
25.(1)计算:﹣3×3﹣1+(﹣2020)0.
(2)以直角三角形中一个锐角的度数为自变量x,另一个锐角度数为因变量y,求y与x之间的关系式.
26.如图,在△ABC中,点D在边AC上,DB=BC,E是CD的中点,F是AB的中点,求证:EF=AB.
27.如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上.
(1)求DM的长.
(2)求旗杆AB的高度.(结果保留根号)
参考答案与试题解析
一.选择题
1.解:由三角形的面积公式可知,CD?AB=AC?BC,A错误,符合题意,D正确,不符合题意;
∵Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD?AB,BC2=BD?AB,B、C正确,不符合题意;
故选:A.
2.解:在Rt△ABC中,
∴sinB===,
故选:C.
3.解:△ABC是锐角三角形,若AB>AC,
则∠C>∠B,
则sinB<sinC.
故选:B.
4.解:∵Rt△ABC中,∠C=90°,
∴cosB==,
设BC=4x,AB=5x,则AC=3x,
∴tanA===.
故选:D.
5.解:sinA==0.2,
所以用科学计算器求这条斜道倾斜角的度数时,
按键顺序为
故选:B.
6.解:∵直角三角形一个锐角的度数为40°,
∴它的另一个内角(锐角)的度数为90°﹣40°=50°,
故选:C.
7.解:过P作PC⊥MN于C,如图所示:
∵PM=PN,MN=5,
∴CM=NC=MN=2.5,
在Rt△OPC中,∠AOB=60°,
∴∠OPC=30°,
∴OC=OP=4,
则OM=OC+CM=4+2.5=6.5,
故选:B.
8.解:作CE⊥AB交AB
的延长线于E,
∵∠ABC=150°,
∴∠CBE=30°,
∴CE=BC=4m.
故选:C.
9.解:∵边长为4的等边△ABC中,CD⊥AB于点D,
∴∠ADC=90°,且AC=AB=4.
又∵E为AC中点,
∴DE=AC=2.
故选:B.
10.解:如图,过点A作AH⊥BC于H.
在Rt△ACH中,∵AH=4,CH=3,
∴AC===5,
∴cos∠ACB==,
故选:C.
二.填空题
11.解:如图所示,设∠A=α,
∵sin,
∴=,
设BC=4x,AB=5x,
∴AC=3x,
则tanα===,
故答案为:.
12.解:在Rt△ABC中,∵∠C=90°,AC=4,BC=6,
∴AB===2,
则sinA===,
故答案为:.
13.解:如图,过点A作AC⊥BD于点C,
根据题意可知:
∠BAC=∠ABC=45°,∠ADC=30°,AB=20,
在Rt△ABC中,AC=BC=AB?sin45°=20×=10,
在Rt△ACD中,∠ADC=30°,
∴AD=2AC=20(海里).
答:此时轮船与小岛的距离AD为20海里.
故答案为:20.
14.解:∵≈0.6180,sin37.5°≈0.6088,
∴>sin37.5°.
故答案为:>.
15.解:∵sin60°=,
∴α+15°=60°,
∴α=45°,
∴tanα=tan45°=1,
故答案为:1.
16.解:由题意得:BE∥桌面,
∴∠α=∠ABE,
∵四边形ABCD是矩形,
∴∠C=90°,AB∥CD,
∴∠BEC=∠ABE,
∵BC=6,BE=12,
∴BC=BE,
∴∠BEC=30°,
∴∠α=∠ABE=∠BEC=30°,
故答案为:30.
17.解:由三角形的三边关系可得三边为6cm,6cm,3cm,其周长为6+6+3=15cm,
分两种情况:(1)当50°的角为顶角时,底角为(180°﹣50°)÷2=65°,
(2)当50°的角为底角时,顶角为180°﹣50°×2=80°,
故答案为:15,50°或80°.
18.解:过F作FM⊥DE于M,
∵CD⊥AB,BE⊥AC,
∴∠BDC=90°,∠BEC=90°,
∵F为BC的中点,BC=10,
∴DF=BC=5,EF=BC=5,
∴DF=EF,
∵FM⊥DE,DE=8,
∴DM=EM=4,
由勾股定理得:FM===3,
∴△DEF的面积是==12,
故答案为:12.
19.解:如图,有三种情形:
①当AC=AD时,∵△ABC中,∠B=70°,∠ACB=90°,
∴∠CAB=20°,
∵AC=AD,
∴∠ADC=∠DCA=(180°﹣∠CAB)=80°;
②当CD′=AD′时,
∵∠CAB=20°,
∴∠D′CA=∠CAB=20°,
∴∠AD′C=180°﹣20°﹣20°=140°.
③当AC=AD″时,则∠AD″C=∠ACD″,
∵∠CAB=20°,∠AD″C+∠ACD″=∠CAB,
∴∠AD″C=10°,
故答案为:80°或140°或10°.
20.解:如图,
∵BD⊥C,
∴∠ADB=∠BDC=90°,
∵∠ABC=90°,
∴∠ABD+∠CBD=90°,∠A+∠ABD=90°,
∴∠A=∠CBD,
∴△ADB∽△BDC,
∴=,
∵AD=2cm,CD=4cm,
∴BD2=AD?CD=2×4=8,
∵BD>0,
∴BD=2(cm),
故答案为:2cm.
三.解答题
21.解:∵∠A为锐角,且sinA=,
∴∠A=30°,
∴cosA=,2sinA﹣cosA=2×﹣=1﹣,
∴4sin2A﹣4sinAcosA+cos2A
=(2sinA﹣cosA)2
=(1﹣)2
=1﹣+
=﹣.
22.解:(1)原式=135××0.224
95
≈135×3.605×0.225
≈371293×3.605×0.225
≈301165.0;
(2)∵α是锐角,且sin(α+15°)=,
∴α+15°=60°,
∴α=45°,
∴原式=2﹣4×﹣1+1+3=3;
故答案为:(1)301165.0;
23.解:(1)如图所示,CD即为所求;
(2)∵CD⊥AB,∠ACB=90°,
∴CD2=AD?DB,
∵AD=2,DB=4,
∴CD=2.
24.解:过点C作CD⊥AB,垂足为D,
在Rt△ACD中,∠A=30°,AC=12,
∴CD=AC=6,
AD=AC=6,
在Rt△BCD中,CD=6,cosB=,
∴=,
设BD=4x,则BC=5x,由勾股定理得,
62+(4x)2=(5x)2,
解得x=2或x=﹣2(舍去),
∴BD=4x=8,
∴S△ABC=AB?CD=(6+8)×6=18+24,
答:△ABC的面积为18+24.
25.(1)解:原式=﹣1+1=0;
(2)解:∵x+y=90,
∴y=90﹣x.
26.证明:连结BE,
∵DB=BC,E是CD的中点,
∴BE⊥AC,
∴∠BEA=90°,
∵F是AB的中点,
∴EF=AB.
27.解:(1)∵CD=2,tan∠CMD=,
∴MD=6m;
(2)过点C作CE⊥AB于点E,
设BM=x,
∴BD=x+6,
∵∠AMB=60°,
∴∠BAM=30°,
∴AB=x,
已知四边形CDBE是矩形,
∴BE=CD=2,CE=BD=x+6,
∴AE=AB﹣BE=x﹣2,
在Rt△ACE中,
∵tan30°=,
∴=,
解得:x=3+,
∴AB=x=(3+3)(m).
解直角三角形》单元测试卷
一.选择题
1.如图,已知在Rt△ABC中,∠ACB=90°,CD⊥AB于D,则下列结论错误的是( )
A.CD?AC=AB?BC
B.AC2=AD?AB
C.BC2=BD?AB
D.AC?BC=AB?CD
2.如图,在Rt△ABC中,∠C=90°,AB=10,AC=6,则sinB等于( )
A.
B.
C.
D.
3.已知△ABC是锐角三角形,若AB>AC,则( )
A.sinA<sinB
B.sinB<sinC
C.sinA<sinC
D.sinC<sinA
4.在Rt△ABC中,∠C=90°,若cosB=,则tanA的值是( )
A.
B.
C.
D.
5.如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道,用科学计算器计算这条斜道的倾斜角,下列按键顺序正确的是( )
A.
B.
C.
D.
6.已知直角三角形一个锐角的度数为40°,则它的另一个内角(锐角)的度数为( )
A.140°
B.60°
C.50°
D.40°
7.如图,已知∠AOB=60°,P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=5,则ON的长度是( )
A.9
B.6.5
C.6
D.5.5
8.如图,某商场一楼与二楼之间的电梯示意图.∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.
m
B.4m
C.4m
D.8m
9.如图,边长为4的等边△ABC中,CD⊥AB于点D,E为AC中点,则DE的长是( )
A.1
B.2
C.
D.2.5
10.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么cos∠ACB值为( )
A.
B.
C.
D.
二.填空题
11.如果∠α是锐角,且sin,那么tanα的值是
.
12.如图,Rt△ABC中,∠C=90°,AC=4,BC=6,则sinA=
.
13.如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为
海里.
14.用科学计算器计算
sin37.5°(比较大小)
15.已知α为锐角,且满足sin(α+15°)=,则tanα=
.
16.如图,将一个装有水的杯子斜放在水平的桌面上,其截面可看作一个宽BC=6厘米的矩形.当水面触到杯口边缘时,水面宽度BE=12厘米,此时杯子的倾斜角α等于
度.
17.已知等腰三角形的两边长分别为6cm和3cm,则此它周长是
cm;已知等腰三角形的一个内角为50°,则它的顶角为
°.
18.如图,在△ABC中,CD⊥AB交AB于点D,BE⊥AC交AC于点E,F为BC的中点,BC=10,DE=8,则△DEF的面积为
.
19.如图,△ABC中,∠B=70°,∠C=90°,在射线BA上找一点D,使△ACD为等腰三角形,则∠ADC的度数为
.
20.在△ABC中,∠ABC=90°,BD⊥AC.若AD=2cm,DC=4cm,则BD=
.
三.解答题
21.已知∠A为锐角且sinA=,则4sin2A﹣4sinAcosA+cos2A的值是多少.
22.选做题(从下面两题中任选一题,如果做了两题的,只按第(2)题评分)
(1)用科学计算器计算:135×sin13°≈
(结果精确到0.1)
(2)已知α是锐角,且sin(α+15°)=.计算﹣4cosα﹣(π﹣3.14)0+tanα+()﹣1的值
23.如图,已知△ABC,∠ACB=90°.
(1)求作AB边上的高CD.(尺规作图,保留作图痕迹,不写作法)
(2)若AD=2,BD=4,求高CD的长.
24.如图,在△ABC中,∠A=30°,cosB=,AC=12,求△ABC的面积.
25.(1)计算:﹣3×3﹣1+(﹣2020)0.
(2)以直角三角形中一个锐角的度数为自变量x,另一个锐角度数为因变量y,求y与x之间的关系式.
26.如图,在△ABC中,点D在边AC上,DB=BC,E是CD的中点,F是AB的中点,求证:EF=AB.
27.如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上.
(1)求DM的长.
(2)求旗杆AB的高度.(结果保留根号)
参考答案与试题解析
一.选择题
1.解:由三角形的面积公式可知,CD?AB=AC?BC,A错误,符合题意,D正确,不符合题意;
∵Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD?AB,BC2=BD?AB,B、C正确,不符合题意;
故选:A.
2.解:在Rt△ABC中,
∴sinB===,
故选:C.
3.解:△ABC是锐角三角形,若AB>AC,
则∠C>∠B,
则sinB<sinC.
故选:B.
4.解:∵Rt△ABC中,∠C=90°,
∴cosB==,
设BC=4x,AB=5x,则AC=3x,
∴tanA===.
故选:D.
5.解:sinA==0.2,
所以用科学计算器求这条斜道倾斜角的度数时,
按键顺序为
故选:B.
6.解:∵直角三角形一个锐角的度数为40°,
∴它的另一个内角(锐角)的度数为90°﹣40°=50°,
故选:C.
7.解:过P作PC⊥MN于C,如图所示:
∵PM=PN,MN=5,
∴CM=NC=MN=2.5,
在Rt△OPC中,∠AOB=60°,
∴∠OPC=30°,
∴OC=OP=4,
则OM=OC+CM=4+2.5=6.5,
故选:B.
8.解:作CE⊥AB交AB
的延长线于E,
∵∠ABC=150°,
∴∠CBE=30°,
∴CE=BC=4m.
故选:C.
9.解:∵边长为4的等边△ABC中,CD⊥AB于点D,
∴∠ADC=90°,且AC=AB=4.
又∵E为AC中点,
∴DE=AC=2.
故选:B.
10.解:如图,过点A作AH⊥BC于H.
在Rt△ACH中,∵AH=4,CH=3,
∴AC===5,
∴cos∠ACB==,
故选:C.
二.填空题
11.解:如图所示,设∠A=α,
∵sin,
∴=,
设BC=4x,AB=5x,
∴AC=3x,
则tanα===,
故答案为:.
12.解:在Rt△ABC中,∵∠C=90°,AC=4,BC=6,
∴AB===2,
则sinA===,
故答案为:.
13.解:如图,过点A作AC⊥BD于点C,
根据题意可知:
∠BAC=∠ABC=45°,∠ADC=30°,AB=20,
在Rt△ABC中,AC=BC=AB?sin45°=20×=10,
在Rt△ACD中,∠ADC=30°,
∴AD=2AC=20(海里).
答:此时轮船与小岛的距离AD为20海里.
故答案为:20.
14.解:∵≈0.6180,sin37.5°≈0.6088,
∴>sin37.5°.
故答案为:>.
15.解:∵sin60°=,
∴α+15°=60°,
∴α=45°,
∴tanα=tan45°=1,
故答案为:1.
16.解:由题意得:BE∥桌面,
∴∠α=∠ABE,
∵四边形ABCD是矩形,
∴∠C=90°,AB∥CD,
∴∠BEC=∠ABE,
∵BC=6,BE=12,
∴BC=BE,
∴∠BEC=30°,
∴∠α=∠ABE=∠BEC=30°,
故答案为:30.
17.解:由三角形的三边关系可得三边为6cm,6cm,3cm,其周长为6+6+3=15cm,
分两种情况:(1)当50°的角为顶角时,底角为(180°﹣50°)÷2=65°,
(2)当50°的角为底角时,顶角为180°﹣50°×2=80°,
故答案为:15,50°或80°.
18.解:过F作FM⊥DE于M,
∵CD⊥AB,BE⊥AC,
∴∠BDC=90°,∠BEC=90°,
∵F为BC的中点,BC=10,
∴DF=BC=5,EF=BC=5,
∴DF=EF,
∵FM⊥DE,DE=8,
∴DM=EM=4,
由勾股定理得:FM===3,
∴△DEF的面积是==12,
故答案为:12.
19.解:如图,有三种情形:
①当AC=AD时,∵△ABC中,∠B=70°,∠ACB=90°,
∴∠CAB=20°,
∵AC=AD,
∴∠ADC=∠DCA=(180°﹣∠CAB)=80°;
②当CD′=AD′时,
∵∠CAB=20°,
∴∠D′CA=∠CAB=20°,
∴∠AD′C=180°﹣20°﹣20°=140°.
③当AC=AD″时,则∠AD″C=∠ACD″,
∵∠CAB=20°,∠AD″C+∠ACD″=∠CAB,
∴∠AD″C=10°,
故答案为:80°或140°或10°.
20.解:如图,
∵BD⊥C,
∴∠ADB=∠BDC=90°,
∵∠ABC=90°,
∴∠ABD+∠CBD=90°,∠A+∠ABD=90°,
∴∠A=∠CBD,
∴△ADB∽△BDC,
∴=,
∵AD=2cm,CD=4cm,
∴BD2=AD?CD=2×4=8,
∵BD>0,
∴BD=2(cm),
故答案为:2cm.
三.解答题
21.解:∵∠A为锐角,且sinA=,
∴∠A=30°,
∴cosA=,2sinA﹣cosA=2×﹣=1﹣,
∴4sin2A﹣4sinAcosA+cos2A
=(2sinA﹣cosA)2
=(1﹣)2
=1﹣+
=﹣.
22.解:(1)原式=135××0.224
95
≈135×3.605×0.225
≈371293×3.605×0.225
≈301165.0;
(2)∵α是锐角,且sin(α+15°)=,
∴α+15°=60°,
∴α=45°,
∴原式=2﹣4×﹣1+1+3=3;
故答案为:(1)301165.0;
23.解:(1)如图所示,CD即为所求;
(2)∵CD⊥AB,∠ACB=90°,
∴CD2=AD?DB,
∵AD=2,DB=4,
∴CD=2.
24.解:过点C作CD⊥AB,垂足为D,
在Rt△ACD中,∠A=30°,AC=12,
∴CD=AC=6,
AD=AC=6,
在Rt△BCD中,CD=6,cosB=,
∴=,
设BD=4x,则BC=5x,由勾股定理得,
62+(4x)2=(5x)2,
解得x=2或x=﹣2(舍去),
∴BD=4x=8,
∴S△ABC=AB?CD=(6+8)×6=18+24,
答:△ABC的面积为18+24.
25.(1)解:原式=﹣1+1=0;
(2)解:∵x+y=90,
∴y=90﹣x.
26.证明:连结BE,
∵DB=BC,E是CD的中点,
∴BE⊥AC,
∴∠BEA=90°,
∵F是AB的中点,
∴EF=AB.
27.解:(1)∵CD=2,tan∠CMD=,
∴MD=6m;
(2)过点C作CE⊥AB于点E,
设BM=x,
∴BD=x+6,
∵∠AMB=60°,
∴∠BAM=30°,
∴AB=x,
已知四边形CDBE是矩形,
∴BE=CD=2,CE=BD=x+6,
∴AE=AB﹣BE=x﹣2,
在Rt△ACE中,
∵tan30°=,
∴=,
解得:x=3+,
∴AB=x=(3+3)(m).
