人教版八年级上册15.1.2分式的基本性质课件
文档属性
| 名称 | 人教版八年级上册15.1.2分式的基本性质课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 861.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 19:31:50 | ||
图片预览




文档简介
15.1.2分式的基本性质
教学重难点
1.了解分式的基本性质。
2.运用“性质”进行分式的约分。
教学目标
重点:理解并掌握分式的基本性质。
难点:灵活运用分式的基本性质,进行
分式约分。
1、什么是分式?
2、何时分式有意义?
3、何时分式值为0?
知识回顾
(一)情景引入、发现新知
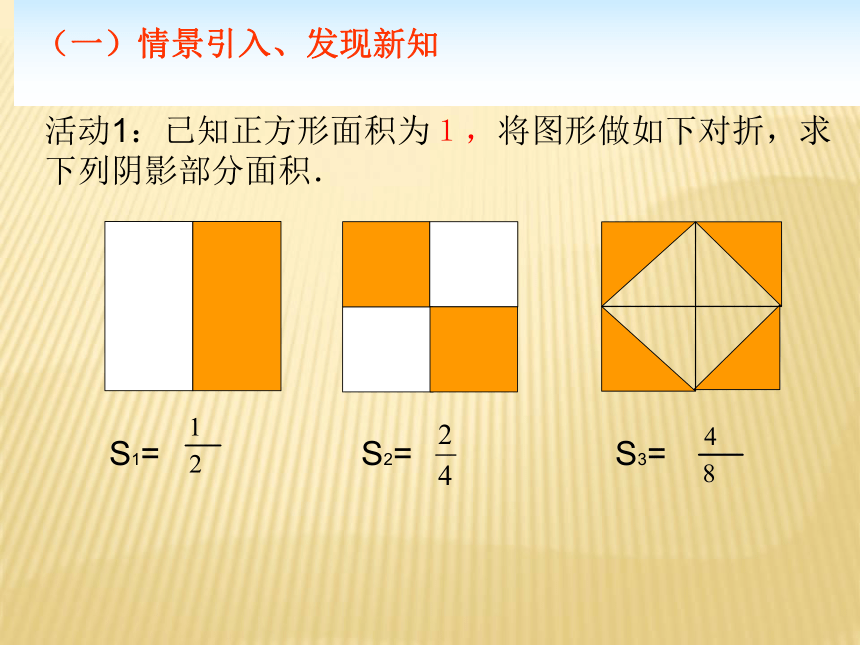
活动1:已知正方形面积为1,将图形做如下对折,求下列阴影部分面积.
S1= S2= S3=
观察:
问题1.这些面积是否相等?
问题2.分数的基本性质是什么?怎样用式子表示?
结论:
分数的基本性质:一个分数的分子、分母同乘(或除以)一个不为0的数,分数的值不变。
S1= S2= S3=
可以进行变形的依据是什么?
(一)情景引入、发现新知
S1= S2= S3=
结论:
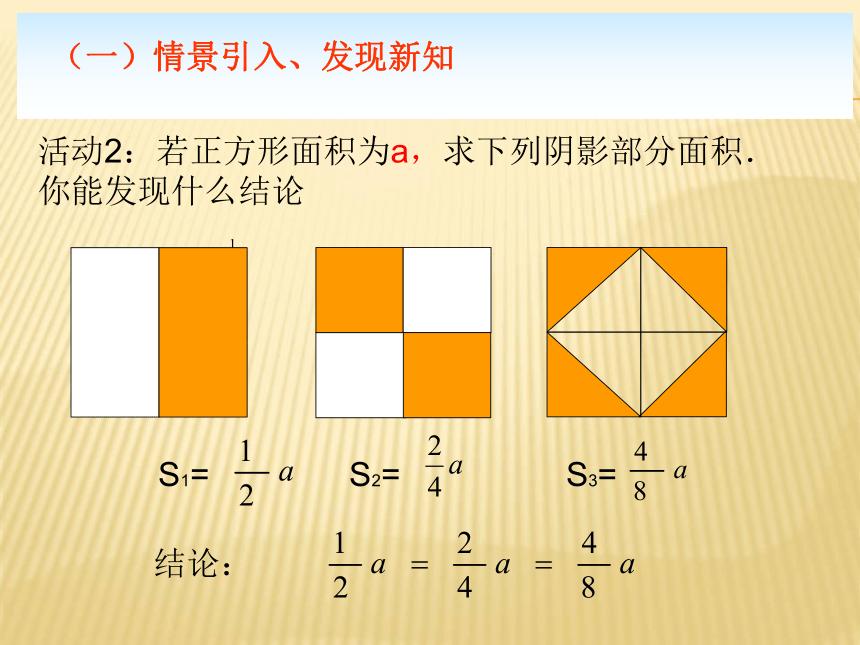
活动2:若正方形面积为a,求下列阴影部分面积.
你能发现什么结论
(一)情景引入、发现新知
S1= S2= S3=
结论:
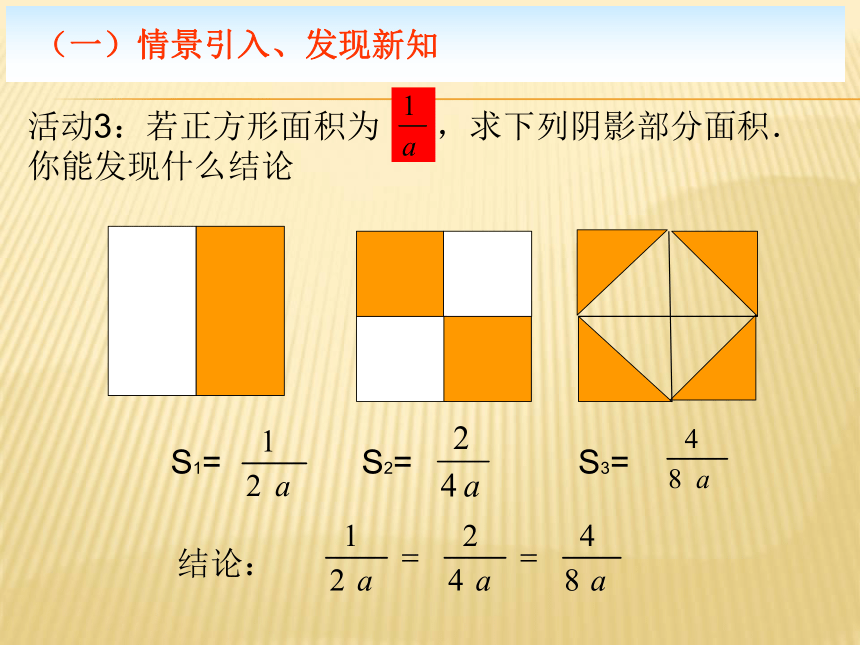
活动3:若正方形面积为 ,求下列阴影部分面积.
你能发现什么结论
问题(1)上式由左边到右边是如何变形的?
(一)情景引入、发现新知
问题(2)上式由右边到左边又是如何变形?
你发现了什么?
(二) 启发诱导 探索新知
类比分数的基本性质,你发现分式有什么性质?
(二) 启发诱导 探索新知
分式的基本性质:分式的分子、分母同时乘(或除以)同一个不为零的整式 ,分式的值不变.
其中A,B,C是整式。
特别强调:C ≠0
例1?.下列等式是怎样从左边得到右边的?
(1)
(2)
由 ,
知 .
解: (1)
(2)
由
知
为什么给出 ?
为什么本题未给 ?
(三) 新知应用
探究新知
类比分数的变形,
像这样,根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.经过约分后的分式 ,其分子与分母没有公因式.像这样分子与分母没有公因式的式子,叫做最简分式.
问题 观察上题中的两个分式的分子、分母的变化,
你联想到什么?
运用新知
例2 约分:
追问1 由上例你能归纳出在分式中,找分子和分母的公因式的方法是什么吗?
追问2 如果分式的分子或分母是多项式,那么该如何思考呢?
归 纳
拓展提升
约分:
分式
B 中
含有字母
方程
运算
有意义
无意义
值为0
概念
基本性质
应用
约分
通分
(五) 小结新知、画龙点睛
谢 谢
教学重难点
1.了解分式的基本性质。
2.运用“性质”进行分式的约分。
教学目标
重点:理解并掌握分式的基本性质。
难点:灵活运用分式的基本性质,进行
分式约分。
1、什么是分式?
2、何时分式有意义?
3、何时分式值为0?
知识回顾
(一)情景引入、发现新知
活动1:已知正方形面积为1,将图形做如下对折,求下列阴影部分面积.
S1= S2= S3=
观察:
问题1.这些面积是否相等?
问题2.分数的基本性质是什么?怎样用式子表示?
结论:
分数的基本性质:一个分数的分子、分母同乘(或除以)一个不为0的数,分数的值不变。
S1= S2= S3=
可以进行变形的依据是什么?
(一)情景引入、发现新知
S1= S2= S3=
结论:
活动2:若正方形面积为a,求下列阴影部分面积.
你能发现什么结论
(一)情景引入、发现新知
S1= S2= S3=
结论:
活动3:若正方形面积为 ,求下列阴影部分面积.
你能发现什么结论
问题(1)上式由左边到右边是如何变形的?
(一)情景引入、发现新知
问题(2)上式由右边到左边又是如何变形?
你发现了什么?
(二) 启发诱导 探索新知
类比分数的基本性质,你发现分式有什么性质?
(二) 启发诱导 探索新知
分式的基本性质:分式的分子、分母同时乘(或除以)同一个不为零的整式 ,分式的值不变.
其中A,B,C是整式。
特别强调:C ≠0
例1?.下列等式是怎样从左边得到右边的?
(1)
(2)
由 ,
知 .
解: (1)
(2)
由
知
为什么给出 ?
为什么本题未给 ?
(三) 新知应用
探究新知
类比分数的变形,
像这样,根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.经过约分后的分式 ,其分子与分母没有公因式.像这样分子与分母没有公因式的式子,叫做最简分式.
问题 观察上题中的两个分式的分子、分母的变化,
你联想到什么?
运用新知
例2 约分:
追问1 由上例你能归纳出在分式中,找分子和分母的公因式的方法是什么吗?
追问2 如果分式的分子或分母是多项式,那么该如何思考呢?
归 纳
拓展提升
约分:
分式
B 中
含有字母
方程
运算
有意义
无意义
值为0
概念
基本性质
应用
约分
通分
(五) 小结新知、画龙点睛
谢 谢
