人教版七年级上册1.5.1乘方 课件(共31张ppt)
文档属性
| 名称 | 人教版七年级上册1.5.1乘方 课件(共31张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 20:05:10 | ||
图片预览









文档简介
乘 方
导入新课
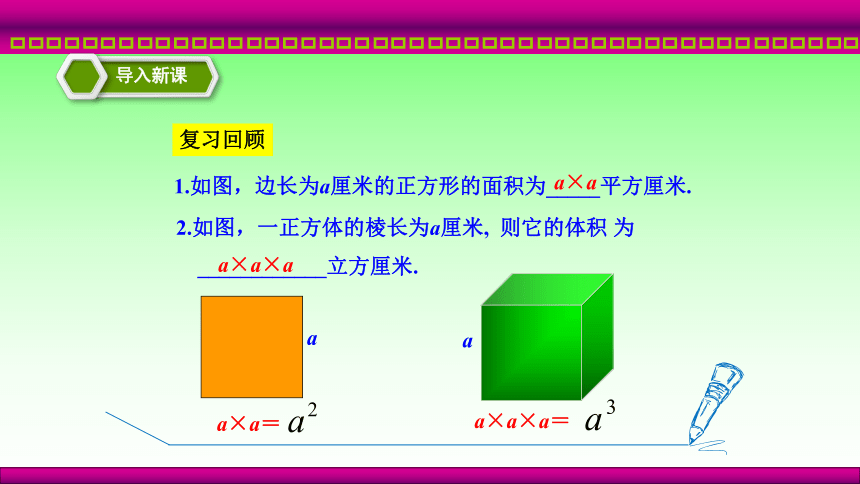
2.如图,一正方体的棱长为a厘米, 则它的体积 为
____________立方厘米.
a×a×a
复习回顾
1.如图,边长为a厘米的正方形的面积为_____平方厘米.
a×a
a
a
a×a=
a×a×a=
导入新课
某种细胞 每30分钟便由一个分裂成两个. 经
过3小时这种细胞由1个能分裂成多少个?
分裂方式如下所示:
1
知识点
有理数的乘方的意义
知1-导
导入新课
知1-导
第一次
第二次
第三次
导入新课
做一做:
这个细胞分裂一次可得多少个细胞?分裂两次呢?
分裂三次呢?四次呢?
那么, 3小时共分裂了多少次?有多少个细胞?
知1-讲
一次得:2个;
两次得:2×2个;
三次得:2×2×2个;
四次得:2×2×2×2个;
六次得:2×2×2×2×2×2个.
答:
请比较细胞分裂四次后的个数式子:2×2×2×2
和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
知1-讲
1. 这两个式子有什么相同点?
答:
它们都是乘法; 并且它们各自的因数都相同.
2.同学们想一想:这样的运算能像平方、立方
那样简写吗?
新课讲解
知1-讲
这样的运算我们可以像平方和立方那样简写:
乘方:求几个相同因数的积的运算,叫做乘方.
2×2×2×2
2×2×2×2×2×2
记作
记作
教学目标
新课讲解
一般地,n个相同的因数a相乘,记作an.即
a×a×a×…×a=an.
n个a
知1-导
新课讲解
知1-导
a
n
底数
幂
指数
a
n
读作a的n次方
看作是a的n次方的结果时,也可读作a的n次幂
新课讲解
知1-讲
其中a代表相乘的因数, n代表相乘因数的个数即:
n个a
an
=
乘方的意义
也就是a的n次方等于n个a相乘
a×a×a···×a
新课讲解
知1-讲
导引:先确定底数,再写成乘方的形式.
例1 把下列各式写成乘方的形式,并指出底数、
指数表示的含义.
(1)(-2)×(-2)×(-2);
(2) × × × ;
(3) × × × × .
新课讲解
知1-讲
解:(1)(-2)×(-2)×(-2)=(-2)3;
底数-2表示相同的因数;
指数3表示相同因数的个数.
(2)
底数 表示相同的因数,
指数4表示相同因数的个数.
(3)
底数 表示相同的因数,
指数5表示相同因数的个数.
新课讲解
总 结
知1-讲
对于有理数的乘除混合运算,应掌握以下几点:
乘方式与乘积式的互化是理解乘方意义的关
键;乘方是一种特殊的乘法运算(因数相同);在将
各个因数都相同的乘法式改为乘方式时,当这个
相同因数是负数、分数,作为底数时,要用括号括
起来.
新课讲解
例2 计算:(1)2100-2101;(2)(0.125)100×8101.
知1-讲
导引:(1)中2100与2101的底数相同,指数接近,实质上
2101=2×2100,可运用乘法分配律计算;(2)中
0.125= ,8101=8×8100,即原题可改为
× 8100×8,100个 的积与100个8的积的积为1.
解:(1) 2100 -2101 =2100-2×2100
=2100×(1-2)=-2100.
(2) (0.125)100×8101 = ×8100×8=1×8=8.
新课讲解
总 结
知1-讲
根据乘方的意义可以将一个指数较大的数转
化为底数相同且指数较小的数的积,如:
2200=2100×2100=2×2199……
巩固提升
1 a3表示( )
A. 3a B. a+a+a
C. a·a·a D. a+3
2 (-3)4表示( )
A.4乘(-3)的积
B.4个(-3)连乘的积
C.3个(-4)连乘的积
D.4个(-3)相加的和
知1-练
C
B
巩固提升
对于-32与(-3)2,下列说法正确的
是( )
A.读法相同,底数不同,结果不同
B.读法不同,底数不同,结果相同
C.读法相同,底数相同,结果不同
D.读法不同,底数不同,结果不同
知1-练
D
教学目标
新课讲解
例3 计算:(1)-(-3)3;
知2-讲
导引:先根据乘方的性质,确定符号,再根据乘方的
意义,把乘方转化为乘法来计算.注意当底数
是带分数时,需先化为假分数,当底数是小数
时,需先化为分数,再进行乘方计算.
2
知识点
有理数的乘方运算
巩固提升
知2-讲
解:(1)-(-3)3=-(-33)=33=3×3×3=27.
(1)-(-3)3;
新课讲解
总 结
知2-讲
有理数乘方的性质是确定乘方结果的符号,
最终的结果还要结合乘方的意义进行计算.
巩固提升
知2-练
1 (中考·郴州)(-3)2计算的结果是( )
A.-6 B.6
C.-9 D.9
2 (中考·孝感)下列各数中,最小的是( )
A.-3 B.|-2|
C.(-3)2 D.2×103
3 如果a的倒数是-1,那么a2 016等于( )
A.1 B.-1
C.2 016 D.-2 016
D
A
A
巩固提升
知2-练
4 下列等式成立的是( )
A.(-3)2=-32 B.-23=(-2)3
C.23=(-2)3 D.32=-32
5 计算:
(1)(-4)3; (2) (-2)4; (3) (- )3.
B
(1)-64;(2)16;(3)
教学目标
新课讲解
解:用带符号键 的计算器.
显示:(-8)^5
-32768.
显示:(-3)^6
729.
所以(-8)5=-32 768, (-3)6=729.
3
知识点
利用计算器计算有理数的乘方
知3-讲
例4 用计算器计算(-8)5和(-3)6.
(-)
)
(-)
(
=
^
8
)
(-)
(
=
^
3
5
6
新课讲解
例5 用计算器计算:
(1)(5.3+8.8)×32- ; (2)1.22;
(3)(-17)7; (4)23×1 .
知3-讲
导引:按算式顺序进行输入,其中一个数的平方
可用 键;负数先按 键,再按数字键.
解:(1)按键顺序为
,
计算器显示的结果为126.3.
x2
(-)
(
5
3
+
8
8
=
)
×
3
x2
-
3
÷
5
.
.
教学目标
新课讲解
知3-讲
(2)按键顺序为 ,
计算器显示的结果为1.44.
(3)按键顺序为 ,
计算器显示的结果为-410 338 673.
(4)按键顺序为 ,
计算器显示的结果为27.6.
=
1
2
x2
)
(
(-)
1
7
7
=
^
.
÷
2
3
×
6
5
=
新课讲解
总 结
知3-讲
用计算器计算时,要弄清计算器的每个按键
的作用,结合有理数运算的顺序,进行计算.
巩固提升
知3-练
1 (1)根据已知条件填空:
①已知(-1.2)2=1.44,
那么(-120)2= ,
(-0.012)2= ;
②已知(-3)3=-27,
那么(-30)3= ,
(-0.3)3= .
14400
0.000144
-27000
-0.027
巩固提升
知3-练
(2)观察上述计算结果我们可以看出:
①当底数的小数点向左(右)每移动一位,它的
平方的幂的小数点向左(右)移动 位;
②当底数的小数点向左(右)每移动一位,它的
立方的幂的小数点向左(右)移动 位.
两
三
课堂小结
1.有理数的乘方运算主要是将它转化为有理数的
乘法来进行计算的,因此它具有如下性质:
(1)负数的奇次幂是负数,负数的偶次幂是正
数;
(2)正数的任何次幂都是正数,0的任何正整
数次幂都是0.
课堂小结
2.“奇负偶正”口诀的应用类型:
有理数的乘方:这里的奇、偶是指指数的奇、偶,
正、负是指幂的符号.例如(-3)2=9,(-3)3
=-27.
谢谢观看!
导入新课
2.如图,一正方体的棱长为a厘米, 则它的体积 为
____________立方厘米.
a×a×a
复习回顾
1.如图,边长为a厘米的正方形的面积为_____平方厘米.
a×a
a
a
a×a=
a×a×a=
导入新课
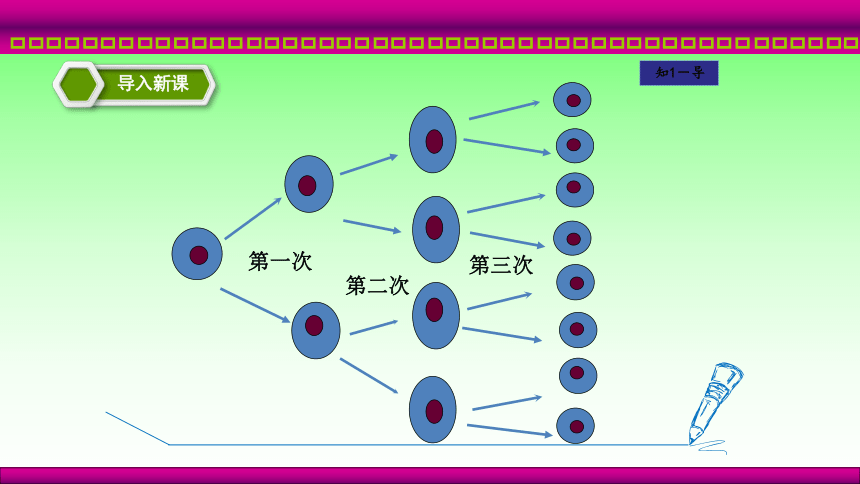
某种细胞 每30分钟便由一个分裂成两个. 经
过3小时这种细胞由1个能分裂成多少个?
分裂方式如下所示:
1
知识点
有理数的乘方的意义
知1-导
导入新课
知1-导
第一次
第二次
第三次
导入新课
做一做:
这个细胞分裂一次可得多少个细胞?分裂两次呢?
分裂三次呢?四次呢?
那么, 3小时共分裂了多少次?有多少个细胞?
知1-讲
一次得:2个;
两次得:2×2个;
三次得:2×2×2个;
四次得:2×2×2×2个;
六次得:2×2×2×2×2×2个.
答:
请比较细胞分裂四次后的个数式子:2×2×2×2
和细胞分裂六次后的个数式子: 2×2×2×2×2×2.
知1-讲
1. 这两个式子有什么相同点?
答:
它们都是乘法; 并且它们各自的因数都相同.
2.同学们想一想:这样的运算能像平方、立方
那样简写吗?
新课讲解
知1-讲
这样的运算我们可以像平方和立方那样简写:
乘方:求几个相同因数的积的运算,叫做乘方.
2×2×2×2
2×2×2×2×2×2
记作
记作
教学目标
新课讲解
一般地,n个相同的因数a相乘,记作an.即
a×a×a×…×a=an.
n个a
知1-导
新课讲解
知1-导
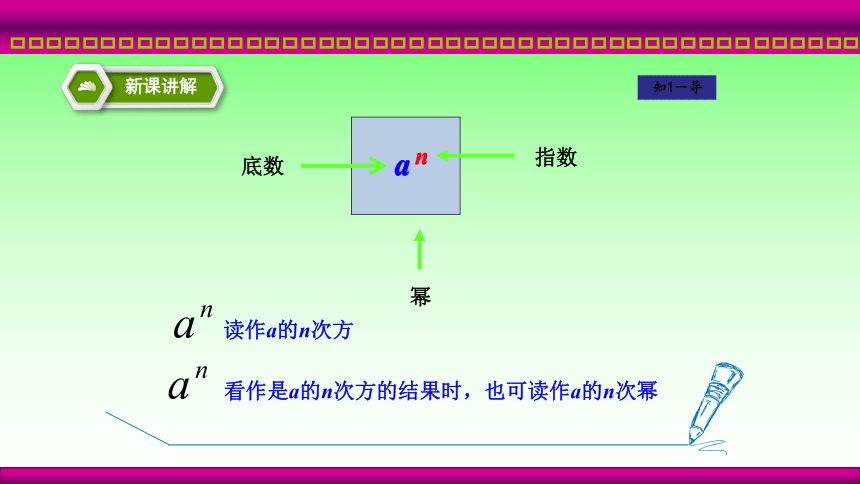
a
n
底数
幂
指数
a
n
读作a的n次方
看作是a的n次方的结果时,也可读作a的n次幂
新课讲解
知1-讲
其中a代表相乘的因数, n代表相乘因数的个数即:
n个a
an
=
乘方的意义
也就是a的n次方等于n个a相乘
a×a×a···×a
新课讲解
知1-讲
导引:先确定底数,再写成乘方的形式.
例1 把下列各式写成乘方的形式,并指出底数、
指数表示的含义.
(1)(-2)×(-2)×(-2);
(2) × × × ;
(3) × × × × .
新课讲解
知1-讲
解:(1)(-2)×(-2)×(-2)=(-2)3;
底数-2表示相同的因数;
指数3表示相同因数的个数.
(2)
底数 表示相同的因数,
指数4表示相同因数的个数.
(3)
底数 表示相同的因数,
指数5表示相同因数的个数.
新课讲解
总 结
知1-讲
对于有理数的乘除混合运算,应掌握以下几点:
乘方式与乘积式的互化是理解乘方意义的关
键;乘方是一种特殊的乘法运算(因数相同);在将
各个因数都相同的乘法式改为乘方式时,当这个
相同因数是负数、分数,作为底数时,要用括号括
起来.
新课讲解
例2 计算:(1)2100-2101;(2)(0.125)100×8101.
知1-讲
导引:(1)中2100与2101的底数相同,指数接近,实质上
2101=2×2100,可运用乘法分配律计算;(2)中
0.125= ,8101=8×8100,即原题可改为
× 8100×8,100个 的积与100个8的积的积为1.
解:(1) 2100 -2101 =2100-2×2100
=2100×(1-2)=-2100.
(2) (0.125)100×8101 = ×8100×8=1×8=8.
新课讲解
总 结
知1-讲
根据乘方的意义可以将一个指数较大的数转
化为底数相同且指数较小的数的积,如:
2200=2100×2100=2×2199……
巩固提升
1 a3表示( )
A. 3a B. a+a+a
C. a·a·a D. a+3
2 (-3)4表示( )
A.4乘(-3)的积
B.4个(-3)连乘的积
C.3个(-4)连乘的积
D.4个(-3)相加的和
知1-练
C
B
巩固提升
对于-32与(-3)2,下列说法正确的
是( )
A.读法相同,底数不同,结果不同
B.读法不同,底数不同,结果相同
C.读法相同,底数相同,结果不同
D.读法不同,底数不同,结果不同
知1-练
D
教学目标
新课讲解
例3 计算:(1)-(-3)3;
知2-讲
导引:先根据乘方的性质,确定符号,再根据乘方的
意义,把乘方转化为乘法来计算.注意当底数
是带分数时,需先化为假分数,当底数是小数
时,需先化为分数,再进行乘方计算.
2
知识点
有理数的乘方运算
巩固提升
知2-讲
解:(1)-(-3)3=-(-33)=33=3×3×3=27.
(1)-(-3)3;
新课讲解
总 结
知2-讲
有理数乘方的性质是确定乘方结果的符号,
最终的结果还要结合乘方的意义进行计算.
巩固提升
知2-练
1 (中考·郴州)(-3)2计算的结果是( )
A.-6 B.6
C.-9 D.9
2 (中考·孝感)下列各数中,最小的是( )
A.-3 B.|-2|
C.(-3)2 D.2×103
3 如果a的倒数是-1,那么a2 016等于( )
A.1 B.-1
C.2 016 D.-2 016
D
A
A
巩固提升
知2-练
4 下列等式成立的是( )
A.(-3)2=-32 B.-23=(-2)3
C.23=(-2)3 D.32=-32
5 计算:
(1)(-4)3; (2) (-2)4; (3) (- )3.
B
(1)-64;(2)16;(3)
教学目标
新课讲解
解:用带符号键 的计算器.
显示:(-8)^5
-32768.
显示:(-3)^6
729.
所以(-8)5=-32 768, (-3)6=729.
3
知识点
利用计算器计算有理数的乘方
知3-讲
例4 用计算器计算(-8)5和(-3)6.
(-)
)
(-)
(
=
^
8
)
(-)
(
=
^
3
5
6
新课讲解
例5 用计算器计算:
(1)(5.3+8.8)×32- ; (2)1.22;
(3)(-17)7; (4)23×1 .
知3-讲
导引:按算式顺序进行输入,其中一个数的平方
可用 键;负数先按 键,再按数字键.
解:(1)按键顺序为
,
计算器显示的结果为126.3.
x2
(-)
(
5
3
+
8
8
=
)
×
3
x2
-
3
÷
5
.
.
教学目标
新课讲解
知3-讲
(2)按键顺序为 ,
计算器显示的结果为1.44.
(3)按键顺序为 ,
计算器显示的结果为-410 338 673.
(4)按键顺序为 ,
计算器显示的结果为27.6.
=
1
2
x2
)
(
(-)
1
7
7
=
^
.
÷
2
3
×
6
5
=
新课讲解
总 结
知3-讲
用计算器计算时,要弄清计算器的每个按键
的作用,结合有理数运算的顺序,进行计算.
巩固提升
知3-练
1 (1)根据已知条件填空:
①已知(-1.2)2=1.44,
那么(-120)2= ,
(-0.012)2= ;
②已知(-3)3=-27,
那么(-30)3= ,
(-0.3)3= .
14400
0.000144
-27000
-0.027
巩固提升
知3-练
(2)观察上述计算结果我们可以看出:
①当底数的小数点向左(右)每移动一位,它的
平方的幂的小数点向左(右)移动 位;
②当底数的小数点向左(右)每移动一位,它的
立方的幂的小数点向左(右)移动 位.
两
三
课堂小结
1.有理数的乘方运算主要是将它转化为有理数的
乘法来进行计算的,因此它具有如下性质:
(1)负数的奇次幂是负数,负数的偶次幂是正
数;
(2)正数的任何次幂都是正数,0的任何正整
数次幂都是0.
课堂小结
2.“奇负偶正”口诀的应用类型:
有理数的乘方:这里的奇、偶是指指数的奇、偶,
正、负是指幂的符号.例如(-3)2=9,(-3)3
=-27.
谢谢观看!
