人教版数学八年级上册13.3.1等腰三角形的性质 课件(共17张ppt)
文档属性
| 名称 | 人教版数学八年级上册13.3.1等腰三角形的性质 课件(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 375.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 20:02:41 | ||
图片预览




文档简介
第1课时
13.3.1等腰三角形
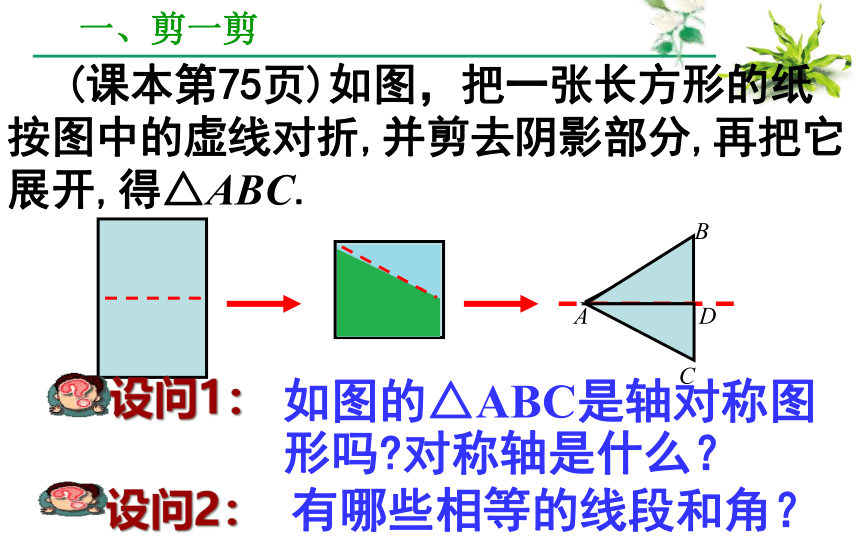
一、剪一剪
(课本第75页)如图,把一张长方形的纸按图中的虚线对折,并剪去阴影部分,再把它展开,得△ABC.
A
C
D
B
如图的△ABC是轴对称图形吗?对称轴是什么?
设问1:
有哪些相等的线段和角?
设问2:
定义的理解:
⑴ 由 得到“等腰三角形”.
A
B
C
∵△ABC中,
∴△ABC是等腰三角形.
AB =AC
⑵ 由“等腰三角形”得到“ 两腰相等 ” .
“两边相等”
∵△ABC是等腰三角形
∴AB=AC.
有两边相等的三角形是等腰三角形
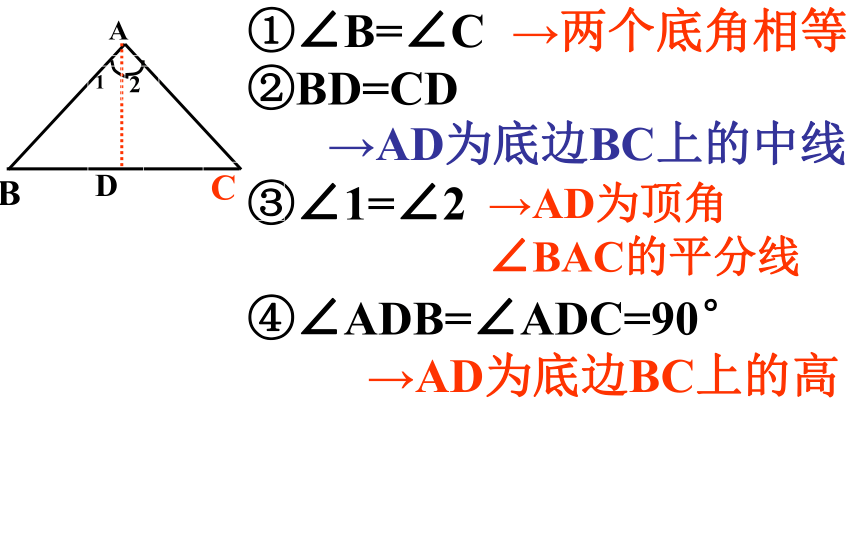
①∠B=∠C
②BD=CD
③∠1=∠2
④∠ADB=∠ADC=90°
1
A
2
C
D
B
→两个底角相等
→AD为底边BC上的中线
→AD为顶角∠BAC的平分线
→AD为底边BC上的高
你能发现等腰三角形有什么性质吗?说一说你的猜想.
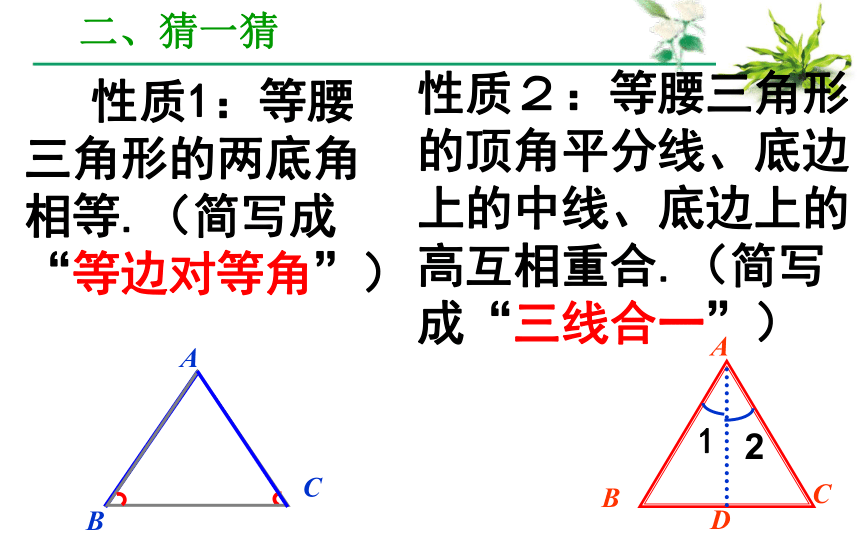
二、猜一猜
性质1:等腰三角形的两底角相等.(简写成“等边对等角”)
C
B
A
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.(简写成“三线合一”)
A
B
C
D
1
2
已知:△ABC中,AB=AC
求证:∠B= ∠C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
等腰三角形的两个底角相等
三、证一证
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角等)
方法一
A
B
C
则∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作BC边上 的高AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角等)
方法二
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法三
作△ABC底边上的中线AD
作△ABC底边
上的高AD
作 △ABC 顶角
的平分线AD.
等腰三角形常见辅助线
D
A
B
C
┌
D
A
B
C
D
A
B
C
40°, 100°
五、用一用
⒈等腰三角形一个底角为40°,它的
另两个角为___ __;
⒊等腰三角形一个顶角为110°,它的
另外两个角为______ __。
⒉等腰三角形一个顶角为80°,它的
另两个角为____ __;
50°, 50°
35°, 35°
40°, 100°或70°, 70°
变式1
变式2
50°, 50°或80°, 20°
变式3
练一练
4.已知等腰三角形的两边长分别是4和6,则它的周长是( )
A、14 B、15
C、16 D、14或16
D
若把此等腰三角形的两边长改为3和7,则它的周长应是多少?
A
B
C
D
例1:如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?
练习:P77练习3
例2:已知一个等腰三角形的两个角分别为(2x-2)°,(3x-5)°. 求这个三角形各内角的度数?
课堂小结
这节课我们学习了什么?
谢谢
13.3.1等腰三角形
一、剪一剪
(课本第75页)如图,把一张长方形的纸按图中的虚线对折,并剪去阴影部分,再把它展开,得△ABC.
A
C
D
B
如图的△ABC是轴对称图形吗?对称轴是什么?
设问1:
有哪些相等的线段和角?
设问2:
定义的理解:
⑴ 由 得到“等腰三角形”.
A
B
C
∵△ABC中,
∴△ABC是等腰三角形.
AB =AC
⑵ 由“等腰三角形”得到“ 两腰相等 ” .
“两边相等”
∵△ABC是等腰三角形
∴AB=AC.
有两边相等的三角形是等腰三角形
①∠B=∠C
②BD=CD
③∠1=∠2
④∠ADB=∠ADC=90°
1
A
2
C
D
B
→两个底角相等
→AD为底边BC上的中线
→AD为顶角∠BAC的平分线
→AD为底边BC上的高
你能发现等腰三角形有什么性质吗?说一说你的猜想.
二、猜一猜
性质1:等腰三角形的两底角相等.(简写成“等边对等角”)
C
B
A
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.(简写成“三线合一”)
A
B
C
D
1
2
已知:△ABC中,AB=AC
求证:∠B= ∠C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
等腰三角形的两个底角相等
三、证一证
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角等)
方法一
A
B
C
则∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作BC边上 的高AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角等)
方法二
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法三
作△ABC底边上的中线AD
作△ABC底边
上的高AD
作 △ABC 顶角
的平分线AD.
等腰三角形常见辅助线
D
A
B
C
┌
D
A
B
C
D
A
B
C
40°, 100°
五、用一用
⒈等腰三角形一个底角为40°,它的
另两个角为___ __;
⒊等腰三角形一个顶角为110°,它的
另外两个角为______ __。
⒉等腰三角形一个顶角为80°,它的
另两个角为____ __;
50°, 50°
35°, 35°
40°, 100°或70°, 70°
变式1
变式2
50°, 50°或80°, 20°
变式3
练一练
4.已知等腰三角形的两边长分别是4和6,则它的周长是( )
A、14 B、15
C、16 D、14或16
D
若把此等腰三角形的两边长改为3和7,则它的周长应是多少?
A
B
C
D
例1:如图,在△ABC中 ,AB=AC,点D在AC 上,且BD=BC=AD. 求△ABC各内角的度数?
练习:P77练习3
例2:已知一个等腰三角形的两个角分别为(2x-2)°,(3x-5)°. 求这个三角形各内角的度数?
课堂小结
这节课我们学习了什么?
谢谢
