人教版数学九年级上册:24.1.1圆-课件
文档属性
| 名称 | 人教版数学九年级上册:24.1.1圆-课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 21:21:19 | ||
图片预览






文档简介
24.1.1 圆
(
(一)创设情境,自主学习
圆是继三角形、四边形等基本图形后的又一个重要内容,圆的有关概念为今后学习圆的知识奠定了基础.
圆是常见的图形,生活中的许多物体都给我们以圆的形象。
(一)创设情境,自主学习
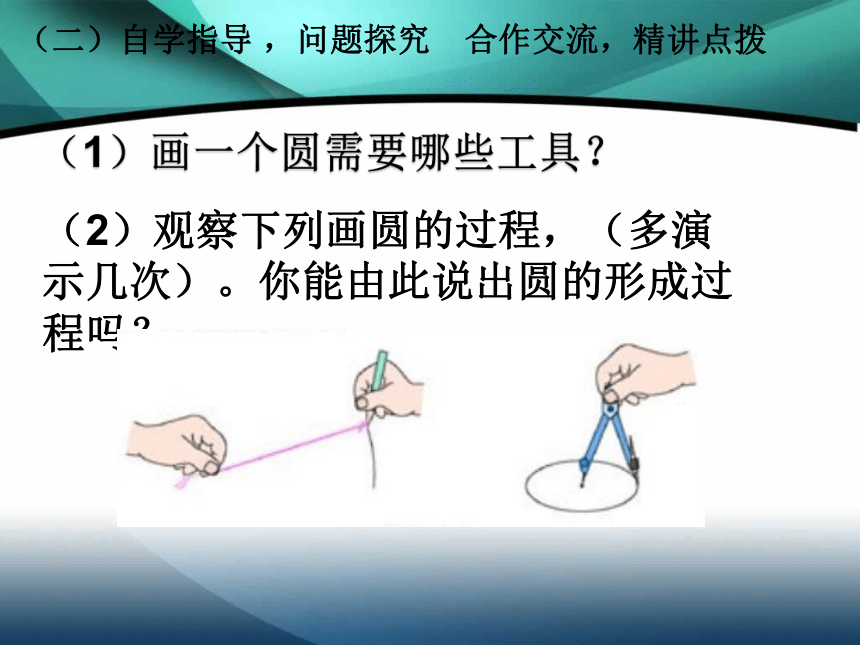
(2)观察下列画圆的过程,(多演示几次)。你能由此说出圆的形成过程吗?
(1)画一个圆需要哪些工具?
(二)自学指导?,问题探究 合作交流,精讲点拨
如图,在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.
·
r
O
A
固定的端点 O 叫做圆心;
线段 OA 叫做半径;
以点 O 为圆心的圆,记作⊙O,读作“圆O”.
圆的概念
(二)自学指导?,问题探究 合作交流,精讲点拨
问题1:圆上各点到定点(圆心 O)的距离有什么规律?
问题2:到定点的距离等于定长的点又有
什么特点?
·
O
A
r
动态:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.
静态:圆心为 O、半径为 r 的圆可以看成是所有到
定点 O 的距离等于定长 r 的点的集合.
圆的第二定义:所有到定点的距离等于定长的点
组成的图形叫做圆.
(二)自学指导?,问题探究 合作交流,精讲点拨
同心圆
等圆
圆心相同,半径不同
确定一个圆的两个要素:
一是圆心,
二是半径.
半径相同,圆心不同
O
(二)自学指导?,问题探究 合作交流,精讲点拨
例:
求证:矩形的四个顶点在以对角线交点为圆心的圆上
已知:矩形ABCD的对角线AC、BD相交于O
求证:A、B、C、D在以O为圆心的同一圆上
证明:∵ABCD是矩形
∴AO=OC;OB=OD
又∵AC=BD
∴OA=OB=OC=OD
∴A、B、C、D在以O为圆心以OA为
半径的圆上。
(二)自学指导?,问题探究 合作交流,精讲点拨
经过圆心的弦叫做直径,如图中的 AB.
连接圆上任意两点的线段叫做弦,如图中的 AC.
弦:
C
O
A
B
(二)自学指导?,问题探究 合作交流,精讲点拨
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
弧
圆上任意两点间的部分叫做圆弧,简称弧.以 A、B 为端点的弧记作 ,读作“圆弧 AB”或“弧 AB”.
AB
等弧
在同圆或等圆中,能重合的弧叫等弧.
(二)自学指导?,问题探究 合作交流,精讲点拨
劣弧与优弧
小于半圆的弧(如图中的 )叫做劣弧.
AC
大于半圆的弧(用三个字母表示,如图中的 )
叫做优弧.
ABC
C
O
A
B
(二)自学指导?,问题探究 合作交流,精讲点拨
C
O
A
B
?
O
检测反馈
如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,求AC的长.
拓展延伸
拓展延伸
如图、已知 在△ABC 中,∠ACB =90°,∠B =25°,以点C 为圆心,CA长为半径的圆交AB于点D,求∠BCD的度数。
本课小结
※ 今天的收获是。。。?
公式法
同学们,再见!
(
(一)创设情境,自主学习
圆是继三角形、四边形等基本图形后的又一个重要内容,圆的有关概念为今后学习圆的知识奠定了基础.
圆是常见的图形,生活中的许多物体都给我们以圆的形象。
(一)创设情境,自主学习
(2)观察下列画圆的过程,(多演示几次)。你能由此说出圆的形成过程吗?
(1)画一个圆需要哪些工具?
(二)自学指导?,问题探究 合作交流,精讲点拨
如图,在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.
·
r
O
A
固定的端点 O 叫做圆心;
线段 OA 叫做半径;
以点 O 为圆心的圆,记作⊙O,读作“圆O”.
圆的概念
(二)自学指导?,问题探究 合作交流,精讲点拨
问题1:圆上各点到定点(圆心 O)的距离有什么规律?
问题2:到定点的距离等于定长的点又有
什么特点?
·
O
A
r
动态:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.
静态:圆心为 O、半径为 r 的圆可以看成是所有到
定点 O 的距离等于定长 r 的点的集合.
圆的第二定义:所有到定点的距离等于定长的点
组成的图形叫做圆.
(二)自学指导?,问题探究 合作交流,精讲点拨
同心圆
等圆
圆心相同,半径不同
确定一个圆的两个要素:
一是圆心,
二是半径.
半径相同,圆心不同
O
(二)自学指导?,问题探究 合作交流,精讲点拨
例:
求证:矩形的四个顶点在以对角线交点为圆心的圆上
已知:矩形ABCD的对角线AC、BD相交于O
求证:A、B、C、D在以O为圆心的同一圆上
证明:∵ABCD是矩形
∴AO=OC;OB=OD
又∵AC=BD
∴OA=OB=OC=OD
∴A、B、C、D在以O为圆心以OA为
半径的圆上。
(二)自学指导?,问题探究 合作交流,精讲点拨
经过圆心的弦叫做直径,如图中的 AB.
连接圆上任意两点的线段叫做弦,如图中的 AC.
弦:
C
O
A
B
(二)自学指导?,问题探究 合作交流,精讲点拨
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
弧
圆上任意两点间的部分叫做圆弧,简称弧.以 A、B 为端点的弧记作 ,读作“圆弧 AB”或“弧 AB”.
AB
等弧
在同圆或等圆中,能重合的弧叫等弧.
(二)自学指导?,问题探究 合作交流,精讲点拨
劣弧与优弧
小于半圆的弧(如图中的 )叫做劣弧.
AC
大于半圆的弧(用三个字母表示,如图中的 )
叫做优弧.
ABC
C
O
A
B
(二)自学指导?,问题探究 合作交流,精讲点拨
C
O
A
B
?
O
检测反馈
如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,求AC的长.
拓展延伸
拓展延伸
如图、已知 在△ABC 中,∠ACB =90°,∠B =25°,以点C 为圆心,CA长为半径的圆交AB于点D,求∠BCD的度数。
本课小结
※ 今天的收获是。。。?
公式法
同学们,再见!
同课章节目录
