人教版数学九年级上册24.1.4 圆周角的概念和圆周角的定理课件(30张)
文档属性
| 名称 | 人教版数学九年级上册24.1.4 圆周角的概念和圆周角的定理课件(30张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 21:29:28 | ||
图片预览





文档简介
在完成探讨圆周角概念、定理和推理任务过程中,你们或许对其“概念、定理、推理”的理解感到困难重重,这节课将对这部分内容进行重点讲解,希望能够给处于困惑中的你们提供帮助,也希望你能更喜欢数学这位“朋友’.
1、复习提问:
(2)圆心角,弧,弦,弦心
距关系定理是什么?
(1)什么是圆心角?
1.圆心角的定义
(1)定义:我们把________在________的角叫做圆心角.
(2)特征:顶点在________
顶点
圆心
2.弧、弦、圆心角、弦心距之间的相等关系(如下:)
圆心
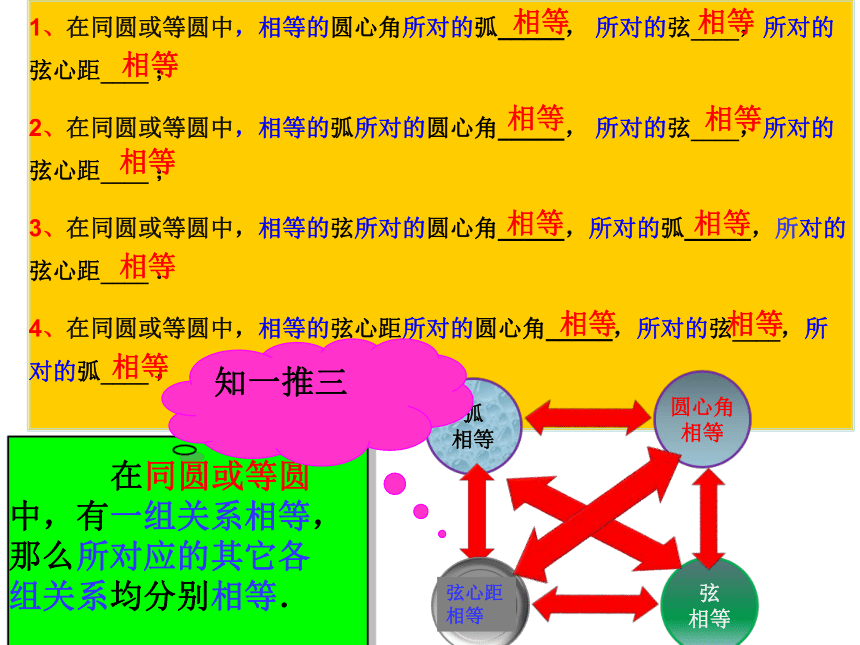
1、在同圆或等圆中,相等的圆心角所对的弧_____, 所对的弦____,所对的弦心距____ ;
2、在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦____,所对的弦心距____ ;
3、在同圆或等圆中,相等的弦所对的圆心角_____,所对的弧_____,所对的弦心距____ .
4、在同圆或等圆中,相等的弦心距所对的圆心角_____,所对的弦____,所对的弧____ ,
相等
相等
相等
相等
相等
相等
相等
相等
相等
弦心距相等
在同圆或等圆中,有一组关系相等,那么所对应的其它各组关系均分别相等.
相等
相等
相等
知一推三
24.1.4 圆周角及其定理和推理
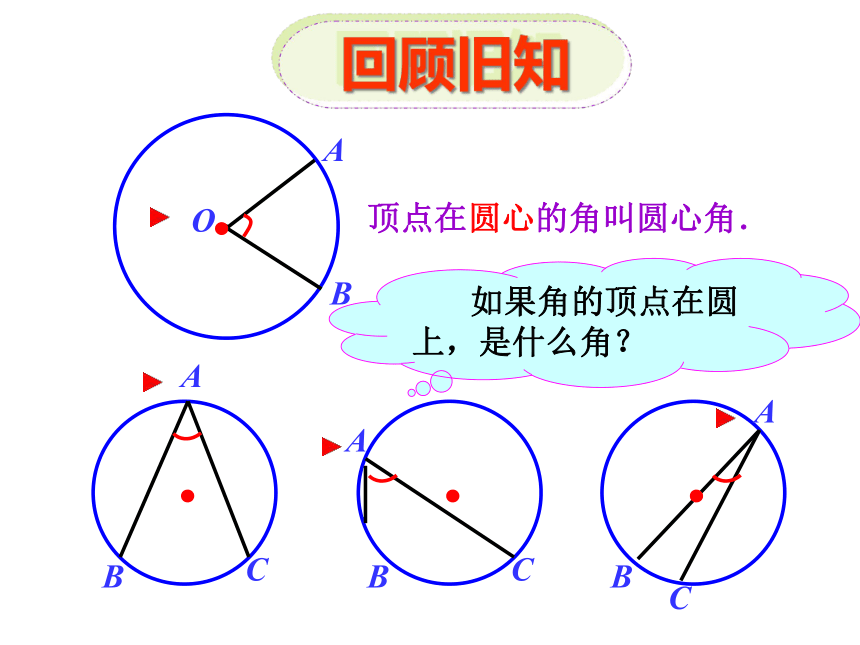
顶点在圆心的角叫圆心角.
·
O
B
A
回顾旧知
A
B
C
A
B
C
A
B
C
如果角的顶点在圆上,是什么角?
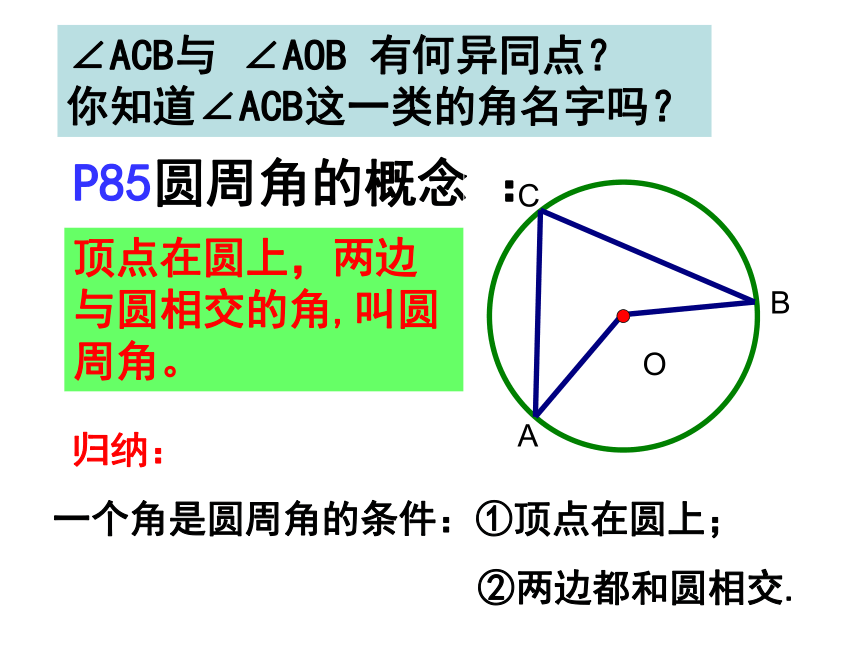
∠ACB与 ∠AOB 有何异同点?
你知道∠ACB这一类的角名字吗?
顶点在圆上,两边与圆相交的角,叫圆周角。
P85圆周角的概念 :
B
A
C
O
归纳:
一个角是圆周角的条件:①顶点在圆上;
②两边都和圆相交.
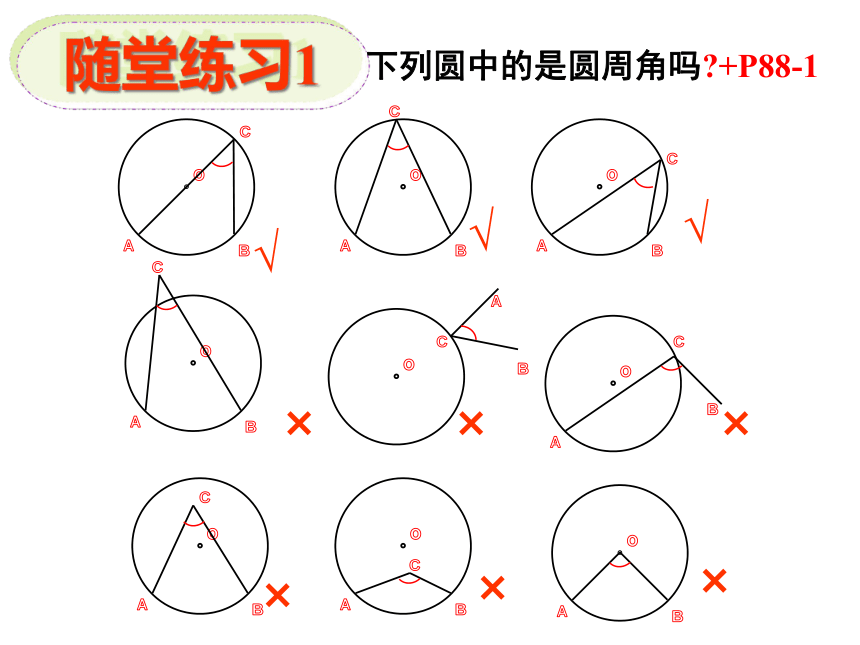
下列圆中的是圆周角吗?+P88-1
√
×
√
×
√
×
×
×
×
随堂练习1
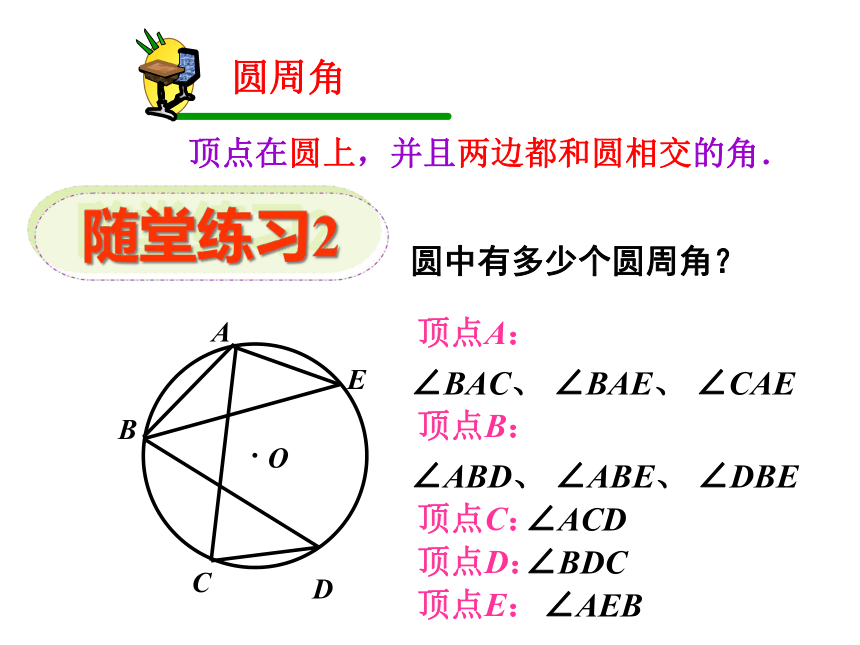
顶点在圆上,并且两边都和圆相交的角.
圆周角
·
E
D
B
A
C
O
圆中有多少个圆周角?
顶点A:
∠BAC、 ∠BAE、 ∠CAE
顶点B:
∠ABD、 ∠ABE、 ∠DBE
顶点C:
∠ACD
顶点D:
顶点E:
∠BDC
∠AEB
随堂练习2
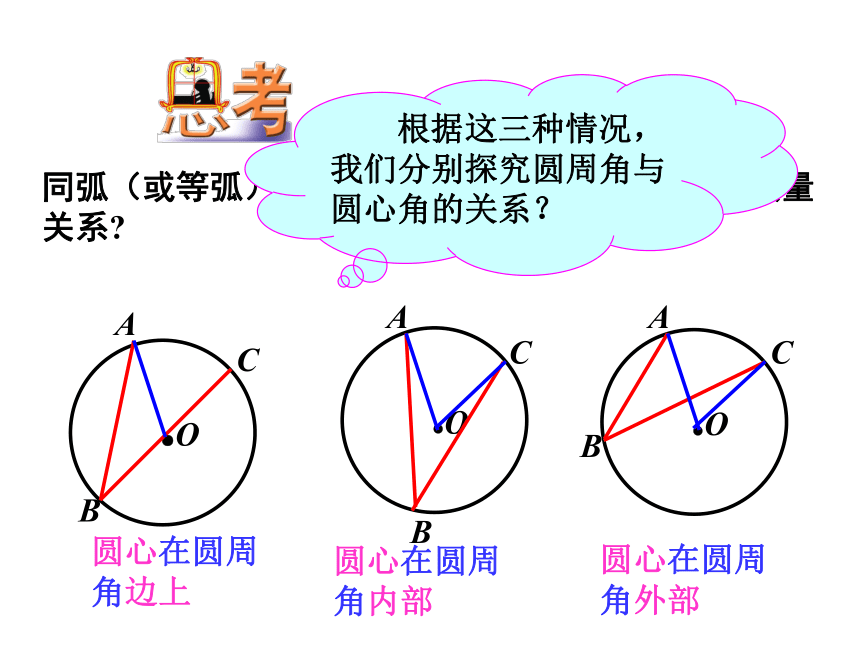
同弧(或等弧)所对的圆周角和圆心角有怎样的数量关系?
●O
A
B
C
●O
A
B
C
●O
A
B
C
根据这三种情况,我们分别探究圆周角与圆心角的关系?
圆心在圆周角边上
圆心在圆周角内部
圆心在圆周角外部
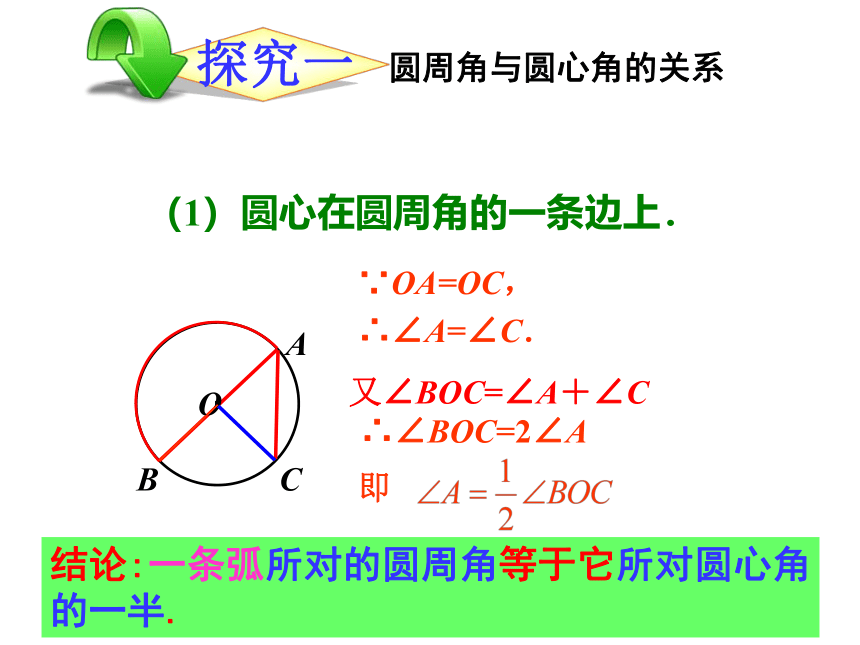
探究一
·
C
O
A
B
即
∵OA=OC,
∴∠A=∠C.
又∠BOC=∠A+∠C
∴∠BOC=2∠A
(1)圆心在圆周角的一条边上.
圆周角与圆心角的关系
结论:一条弧所对的圆周角等于它所对圆心角的一半.
(2)圆心在圆周角的内部.
作直径AD,
利用(1)的结果,有
·
C
O
A
B
D
探究
圆周角与圆心角的关系
结论:一条弧所对的圆周角等于它所对圆心角的一半.
1
2
3
4
5
6
(3)圆心在圆周角的外部.
·
C
O
A
B
D
作直径AD,利用(1)的结果,有
探究
圆周角与圆心角的关系
结论:一条弧所对的圆周角等于它所对圆心角的一半.
五、定理
B
A
C
O
B′
A′
C′
O′
AB=A′B′
⌒ ⌒
五、定理
在同圆或等圆中,一条弧(同弧或等弧)所对的圆周角等于它所对圆心角的一半
圆周角定 理
B
A
C
O
条件“在同圆或等圆中”可以省略吗?
.
说说下图∠AOB、∠C、∠D的数量关系:
练一练
随堂练习3
类比圆心角推导圆周角的性质
在同圆或等圆中,同弧或等弧所对的 圆心角 相等.
圆周角
结论是否成立?
举一反三
五、推理
B
A
C
O
B′
A′
C′
O′
1、如下,两等圆中,
AB=A′B′
⌒ ⌒
2、在同弧中成立吗?即∠C=∠D吗?
五、推理
(同圆或等圆中),同弧或等弧所对圆周角相等
圆周角定理推理1
以上逆命题“同圆或等圆中,相等圆周角所对的弧相等”吗?
条件“在同圆或等圆中”可以省略吗?
五、推理2
B
A
C
O
B'
A'
C′
O′
同圆或等圆中,相等的圆周角所对的弧相等
圆周角定理推理2
条件“在同圆或等圆中”可以省略吗?
·
C
E
B
A
D
知识要点
·
圆周角定理的推理
2、 在同圆或等圆中,如果两个圆周角相等,
它们所对的弧一定相等
1、(在同圆或等圆中),同弧或等弧所对的圆周角相等.
正确理解圆心角,弦、弦心距、圆周角与弧的互推关系
知一推四
前提:同圆或等圆中
P88 2、点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∴∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
解:∵同弧来所对的圆周角相等
随堂练习4
已知∠CAD=∠EBF,则弧CD、弧EF的数量关系是:
D
A
B
O
C
E
F
F
∴ CD=EF
)
)
解:∵ ∠CAD=∠EBF
随堂练习5
课堂小结
顶点在圆上,并且两边都和圆相交的角.
1. 圆周角
2. 圆周角定理
A
B
C
在同圆(或等圆)中,一条弧所对的圆周角等于它所对的圆心角的一半.
(2)在同圆或等圆中,相等的圆周角所对的弧相等。
(1)在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
3. 圆周角定理(推理)
D
A
B
O
C
E
F
F
B
A
C
O
B'
A'
C′
O′
【方法一点通】
利用圆周角定理及其推论证明时常用的思路
1.在同圆或等圆中,要证弧相等,考虑证明这两条弧所对的圆周角(圆心角、弦、弦心距)相等.
2.在同圆或等圆中,要证圆周角相等,考虑证明这两个圆周角所对的弧(圆心角、弦、弦心距)相等.
正确理解圆心角,弦、弦心距、圆周角与弧的互推关系
知一推四
前提:同圆或是等圆中
课后练习.
P88 第3,4题.
谢谢大家!
A
B
C
D
课后作业
1. 已知:AC = BD,
⌒
⌒
求证:AB∥CD.
2.AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35° ,求∠BOC的度数。
1、通过以上的讲解,不知大家是否已经对《圆周角》有了更清晰的认识呢?接下来,大家继续完成你们的任务吧!
2、如果还有任何问题,可以通过打我电话13417088652或是加我QQ5910504033我们继续探讨!或是同学们建个学习群交流学习。
3、如果你对《圆周角》这个知识深感兴趣,想要进一步的学习,可以到以下网址获取更多的相关知识,继续深入研究。
https://www.baidu.com/s?ie=utf-8&f=8&rsv_bp=1&tn=98050039_dg&wd=%E5%9C%86%E5%91%A8%E8%A7%92%E5%AE%9A%E7%90%86%E5%92%8C%E6%8E%A8%E7%90%86&oq=%E5%9C%86%E5%91%A8%E8%A7%92%E5%AE%9A%E7%90%86&rsv_pq=9eb535dc000014e4&rsv_t=68cfYxPyvBdcC0RddPVWsmg%2FzEwqqlPOvnnSfjf1r%2BC2lCTZGKS8HWubuaN3wgHaaRo&rqlang=cn&rsv_enter=1&rsv_sug3=4&rsv_sug1=2&rsv_sug7=100&bs=%E5%9C%86%E5%91%A8%E8%A7%92%E5%AE%9A%E7%90%86
1、复习提问:
(2)圆心角,弧,弦,弦心
距关系定理是什么?
(1)什么是圆心角?
1.圆心角的定义
(1)定义:我们把________在________的角叫做圆心角.
(2)特征:顶点在________
顶点
圆心
2.弧、弦、圆心角、弦心距之间的相等关系(如下:)
圆心
1、在同圆或等圆中,相等的圆心角所对的弧_____, 所对的弦____,所对的弦心距____ ;
2、在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦____,所对的弦心距____ ;
3、在同圆或等圆中,相等的弦所对的圆心角_____,所对的弧_____,所对的弦心距____ .
4、在同圆或等圆中,相等的弦心距所对的圆心角_____,所对的弦____,所对的弧____ ,
相等
相等
相等
相等
相等
相等
相等
相等
相等
弦心距相等
在同圆或等圆中,有一组关系相等,那么所对应的其它各组关系均分别相等.
相等
相等
相等
知一推三
24.1.4 圆周角及其定理和推理
顶点在圆心的角叫圆心角.
·
O
B
A
回顾旧知
A
B
C
A
B
C
A
B
C
如果角的顶点在圆上,是什么角?
∠ACB与 ∠AOB 有何异同点?
你知道∠ACB这一类的角名字吗?
顶点在圆上,两边与圆相交的角,叫圆周角。
P85圆周角的概念 :
B
A
C
O
归纳:
一个角是圆周角的条件:①顶点在圆上;
②两边都和圆相交.
下列圆中的是圆周角吗?+P88-1
√
×
√
×
√
×
×
×
×
随堂练习1
顶点在圆上,并且两边都和圆相交的角.
圆周角
·
E
D
B
A
C
O
圆中有多少个圆周角?
顶点A:
∠BAC、 ∠BAE、 ∠CAE
顶点B:
∠ABD、 ∠ABE、 ∠DBE
顶点C:
∠ACD
顶点D:
顶点E:
∠BDC
∠AEB
随堂练习2
同弧(或等弧)所对的圆周角和圆心角有怎样的数量关系?
●O
A
B
C
●O
A
B
C
●O
A
B
C
根据这三种情况,我们分别探究圆周角与圆心角的关系?
圆心在圆周角边上
圆心在圆周角内部
圆心在圆周角外部
探究一
·
C
O
A
B
即
∵OA=OC,
∴∠A=∠C.
又∠BOC=∠A+∠C
∴∠BOC=2∠A
(1)圆心在圆周角的一条边上.
圆周角与圆心角的关系
结论:一条弧所对的圆周角等于它所对圆心角的一半.
(2)圆心在圆周角的内部.
作直径AD,
利用(1)的结果,有
·
C
O
A
B
D
探究
圆周角与圆心角的关系
结论:一条弧所对的圆周角等于它所对圆心角的一半.
1
2
3
4
5
6
(3)圆心在圆周角的外部.
·
C
O
A
B
D
作直径AD,利用(1)的结果,有
探究
圆周角与圆心角的关系
结论:一条弧所对的圆周角等于它所对圆心角的一半.
五、定理
B
A
C
O
B′
A′
C′
O′
AB=A′B′
⌒ ⌒
五、定理
在同圆或等圆中,一条弧(同弧或等弧)所对的圆周角等于它所对圆心角的一半
圆周角定 理
B
A
C
O
条件“在同圆或等圆中”可以省略吗?
.
说说下图∠AOB、∠C、∠D的数量关系:
练一练
随堂练习3
类比圆心角推导圆周角的性质
在同圆或等圆中,同弧或等弧所对的 圆心角 相等.
圆周角
结论是否成立?
举一反三
五、推理
B
A
C
O
B′
A′
C′
O′
1、如下,两等圆中,
AB=A′B′
⌒ ⌒
2、在同弧中成立吗?即∠C=∠D吗?
五、推理
(同圆或等圆中),同弧或等弧所对圆周角相等
圆周角定理推理1
以上逆命题“同圆或等圆中,相等圆周角所对的弧相等”吗?
条件“在同圆或等圆中”可以省略吗?
五、推理2
B
A
C
O
B'
A'
C′
O′
同圆或等圆中,相等的圆周角所对的弧相等
圆周角定理推理2
条件“在同圆或等圆中”可以省略吗?
·
C
E
B
A
D
知识要点
·
圆周角定理的推理
2、 在同圆或等圆中,如果两个圆周角相等,
它们所对的弧一定相等
1、(在同圆或等圆中),同弧或等弧所对的圆周角相等.
正确理解圆心角,弦、弦心距、圆周角与弧的互推关系
知一推四
前提:同圆或等圆中
P88 2、点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∴∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
解:∵同弧来所对的圆周角相等
随堂练习4
已知∠CAD=∠EBF,则弧CD、弧EF的数量关系是:
D
A
B
O
C
E
F
F
∴ CD=EF
)
)
解:∵ ∠CAD=∠EBF
随堂练习5
课堂小结
顶点在圆上,并且两边都和圆相交的角.
1. 圆周角
2. 圆周角定理
A
B
C
在同圆(或等圆)中,一条弧所对的圆周角等于它所对的圆心角的一半.
(2)在同圆或等圆中,相等的圆周角所对的弧相等。
(1)在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
3. 圆周角定理(推理)
D
A
B
O
C
E
F
F
B
A
C
O
B'
A'
C′
O′
【方法一点通】
利用圆周角定理及其推论证明时常用的思路
1.在同圆或等圆中,要证弧相等,考虑证明这两条弧所对的圆周角(圆心角、弦、弦心距)相等.
2.在同圆或等圆中,要证圆周角相等,考虑证明这两个圆周角所对的弧(圆心角、弦、弦心距)相等.
正确理解圆心角,弦、弦心距、圆周角与弧的互推关系
知一推四
前提:同圆或是等圆中
课后练习.
P88 第3,4题.
谢谢大家!
A
B
C
D
课后作业
1. 已知:AC = BD,
⌒
⌒
求证:AB∥CD.
2.AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35° ,求∠BOC的度数。
1、通过以上的讲解,不知大家是否已经对《圆周角》有了更清晰的认识呢?接下来,大家继续完成你们的任务吧!
2、如果还有任何问题,可以通过打我电话13417088652或是加我QQ5910504033我们继续探讨!或是同学们建个学习群交流学习。
3、如果你对《圆周角》这个知识深感兴趣,想要进一步的学习,可以到以下网址获取更多的相关知识,继续深入研究。
https://www.baidu.com/s?ie=utf-8&f=8&rsv_bp=1&tn=98050039_dg&wd=%E5%9C%86%E5%91%A8%E8%A7%92%E5%AE%9A%E7%90%86%E5%92%8C%E6%8E%A8%E7%90%86&oq=%E5%9C%86%E5%91%A8%E8%A7%92%E5%AE%9A%E7%90%86&rsv_pq=9eb535dc000014e4&rsv_t=68cfYxPyvBdcC0RddPVWsmg%2FzEwqqlPOvnnSfjf1r%2BC2lCTZGKS8HWubuaN3wgHaaRo&rqlang=cn&rsv_enter=1&rsv_sug3=4&rsv_sug1=2&rsv_sug7=100&bs=%E5%9C%86%E5%91%A8%E8%A7%92%E5%AE%9A%E7%90%86
同课章节目录
