人教版数学九年级上册24.4探究圆的弧长、扇形面积公式课件(第一课时 17张)
文档属性
| 名称 | 人教版数学九年级上册24.4探究圆的弧长、扇形面积公式课件(第一课时 17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 860.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 20:38:22 | ||
图片预览





文档简介
24.4 弧长和扇形面积
第1课时
点、直线和圆的位置关系
正多边形和圆
圆的有关性质
弧长和扇形面积
垂径定理
圆心角
圆周角
圆锥面积
三角形的外接圆
三角形的内切圆
切线
弧长扇形面积
有关计算
等分圆周
第
24
章
1.经历探索弧长计算公式及扇形面积计算公式的过程,培养我们的探索能力.
2.了解弧长及扇形面积公式后,能用公式解决问题,加强我们运用数学的能力.
在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位运动员弯路的展直长度相同吗?
情境导入
生成问题
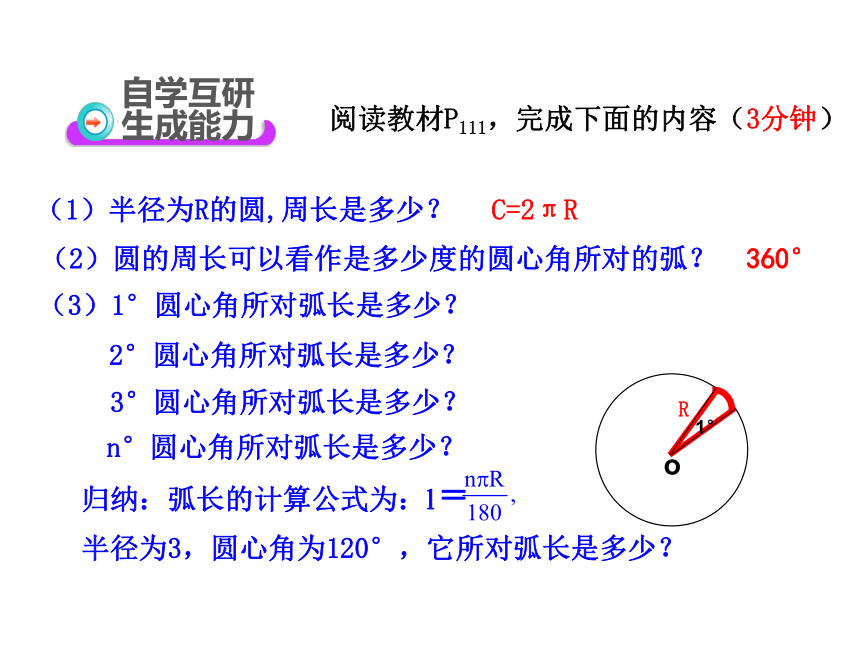
(1)半径为R的圆,周长是多少?
C=2πR
(3)1°圆心角所对弧长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
2°圆心角所对弧长是多少?
3°圆心角所对弧长是多少?
n°圆心角所对弧长是多少?
自学互研
生成能力
阅读教材P111,完成下面的内容(3分钟)
归纳:弧长的计算公式为:l =
1°
o
360°
半径为3,圆心角为120°,它所对弧长是多少?
R
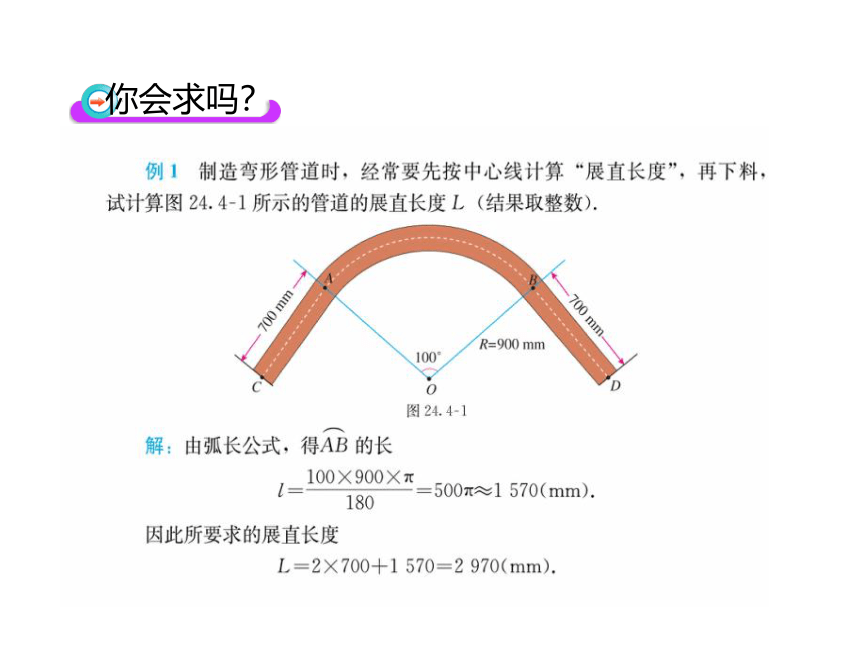
【例1】制造弯形管道时,要先按中心线计算“展直长
度”,再下料,试计算如图所示管道的展直长度l(结果用 表示)
你会求吗?
你会求吗?
1.已知弧所对的圆心角为90°,半径是4,则弧长为____
2. 已知一条弧的半径为9,弧长为8∏,那么这条弧所对的圆心角为_______.
3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )cm
A. B. C. D.
160°
B
跟踪训练
2∏
∏
∏
∏
∏
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形.
n°
o
A
B
O
自学互研
生成能力
A
B
O
(1)半径为R的圆,面积是多少?
S=πR2
(3)1°圆心角所对扇形面积是多少?
(2)圆面可以看作是多少度的圆心角所对的扇形?
若设⊙O半径为R, n°的圆心角所对的扇形面积为S,则
自学互研
生成能力
阅读教材P112例2之前的内容,完成下面各题(2分钟)
360°
扇形的面积公式为:S=
A
B
O
O
比较扇形面积与弧长公式, 你能用弧长表示扇形面积吗?
l=
S=
S扇形
自学互研
生成能力
例2:已知扇形的圆心角是150°,弧长是25π,
求扇形的面积.
你会求吗?
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形=____.
2、已知扇形面积为 ,圆心角为60°,则这个扇形的半径R=____.
3、已知半径为2cm的扇形,其弧长为10cm,则这个扇形的面积S扇形=____cm2.
跟踪训练
2
10
【例2】如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm).
0
B
A
C
D
弓形的面积 = S扇- S△OAB
合作探究
生成能力
提示:
请同学们自己完成.
1.如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.(精确到0.01cm).
0
A
B
D
C
E
弓形的面积 = S扇+ S△OAB
跟踪训练
提示:
当堂检测
达成目标
1.已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是 ,扇形的圆心角为 .
2.已知扇形的半径为3cm,面积为3πcm,则扇形的圆心角是 ,扇形的弧长是 .(结果保留π)
3.如图,半圆的直径AB=10,P为AB上一点,点C、D为半圆的三等分点,则阴影部分的面积为 .
1.弧长的计算公式l= 并运用公式进行计算;
2.扇形的面积公式S= 并运用公式进行计算;
3.弧长l及扇形的面积S之间的关系,
4.会应用知识解决实际问题。
通过本课时的学习,需要我们掌握:
课堂小结
S扇形
第1课时
点、直线和圆的位置关系
正多边形和圆
圆的有关性质
弧长和扇形面积
垂径定理
圆心角
圆周角
圆锥面积
三角形的外接圆
三角形的内切圆
切线
弧长扇形面积
有关计算
等分圆周
第
24
章
1.经历探索弧长计算公式及扇形面积计算公式的过程,培养我们的探索能力.
2.了解弧长及扇形面积公式后,能用公式解决问题,加强我们运用数学的能力.
在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位运动员弯路的展直长度相同吗?
情境导入
生成问题
(1)半径为R的圆,周长是多少?
C=2πR
(3)1°圆心角所对弧长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
2°圆心角所对弧长是多少?
3°圆心角所对弧长是多少?
n°圆心角所对弧长是多少?
自学互研
生成能力
阅读教材P111,完成下面的内容(3分钟)
归纳:弧长的计算公式为:l =
1°
o
360°
半径为3,圆心角为120°,它所对弧长是多少?
R
【例1】制造弯形管道时,要先按中心线计算“展直长
度”,再下料,试计算如图所示管道的展直长度l(结果用 表示)
你会求吗?
你会求吗?
1.已知弧所对的圆心角为90°,半径是4,则弧长为____
2. 已知一条弧的半径为9,弧长为8∏,那么这条弧所对的圆心角为_______.
3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )cm
A. B. C. D.
160°
B
跟踪训练
2∏
∏
∏
∏
∏
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形.
n°
o
A
B
O
自学互研
生成能力
A
B
O
(1)半径为R的圆,面积是多少?
S=πR2
(3)1°圆心角所对扇形面积是多少?
(2)圆面可以看作是多少度的圆心角所对的扇形?
若设⊙O半径为R, n°的圆心角所对的扇形面积为S,则
自学互研
生成能力
阅读教材P112例2之前的内容,完成下面各题(2分钟)
360°
扇形的面积公式为:S=
A
B
O
O
比较扇形面积与弧长公式, 你能用弧长表示扇形面积吗?
l=
S=
S扇形
自学互研
生成能力
例2:已知扇形的圆心角是150°,弧长是25π,
求扇形的面积.
你会求吗?
1、已知扇形的圆心角为120°,半径为2,则这个扇形的面积S扇形=____.
2、已知扇形面积为 ,圆心角为60°,则这个扇形的半径R=____.
3、已知半径为2cm的扇形,其弧长为10cm,则这个扇形的面积S扇形=____cm2.
跟踪训练
2
10
【例2】如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm).
0
B
A
C
D
弓形的面积 = S扇- S△OAB
合作探究
生成能力
提示:
请同学们自己完成.
1.如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.(精确到0.01cm).
0
A
B
D
C
E
弓形的面积 = S扇+ S△OAB
跟踪训练
提示:
当堂检测
达成目标
1.已知扇形的半径为3cm,扇形的弧长为πcm,则该扇形的面积是 ,扇形的圆心角为 .
2.已知扇形的半径为3cm,面积为3πcm,则扇形的圆心角是 ,扇形的弧长是 .(结果保留π)
3.如图,半圆的直径AB=10,P为AB上一点,点C、D为半圆的三等分点,则阴影部分的面积为 .
1.弧长的计算公式l= 并运用公式进行计算;
2.扇形的面积公式S= 并运用公式进行计算;
3.弧长l及扇形的面积S之间的关系,
4.会应用知识解决实际问题。
通过本课时的学习,需要我们掌握:
课堂小结
S扇形
同课章节目录
