人教版八年级数学上册第15章15.2.3 整数指数幂 课件(15张)
文档属性
| 名称 | 人教版八年级数学上册第15章15.2.3 整数指数幂 课件(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 558.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 00:00:00 | ||
图片预览






文档简介
15.2.3 整数指数幂
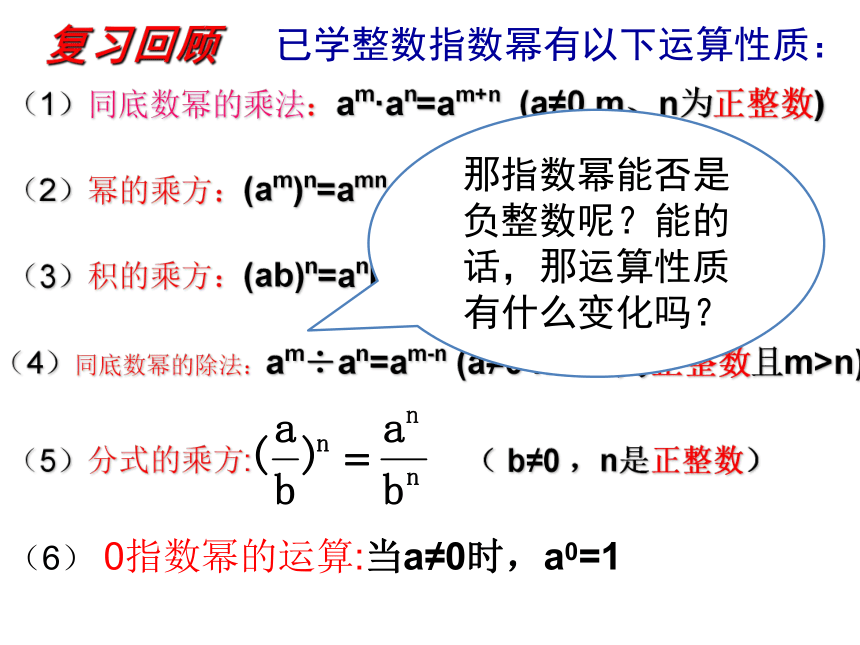
已学整数指数幂有以下运算性质:
(6) 0指数幂的运算:当a≠0时,a0=1
(1)同底数幂的乘法:am·an=am+n (a≠0 m、n为正整数)
(2)幂的乘方:(am)n=amn (a≠0 m、n为正整数)
(3)积的乘方:(ab)n=anbn (a,b≠0 m、n为正整数)
(4)同底数幂的除法:am÷an=am-n (a≠0 m、n为正整数且m>n)
(5)分式的乘方: ( b≠0 ,n是正整数)
那指数幂能否是负整数呢?能的话,那运算性质有什么变化吗?
复习回顾
学习目标(1分钟)
1、理解负整数指数幂的意义
2、掌握整数指数幂的运算性质
3、会运用这一性质进行简单的计算
自学指导一 (5分钟)
阅读教材143页上半部分,思考并回答以下问题:
am÷an=am-n (a≠0, m、n为正整数且m>n)
a5÷a3=a2
a3÷a5=?
a3÷a5=
(a≠0)
也就是说,a-n是an的 .
1、去掉上述法则的适用条件,用上述运算性质可得:
a-2
2、用分式约分可得:
a3÷a5=
3、得出的两结果是什么关系 :
4、你能得到什么结论 :
倒数
点拨运用一 (2分钟)
温馨提示:
公式里面的a可以是不等于0的任何数字或式子。
(a≠0)
也就是说,a-n是an的倒数
1、填空:
9
16
自学检测一(10分钟)
2、利用负整指数幂把下列各式化成不含分母的式子
1、
2、
阅读课本143页如下特例思考:
引入负整数指数和0指数后,m,n 是任意整数是否适用于运算性质 ?
自学指导二 (5分钟)
am·an=am+n (a≠0,m,n是整数 )
am·an=am+n (a≠0 m、n为正整数)
自此指数的取值范围推广到全体整数,这样,整数指数的运算性质可重新归纳为三大类:
(1)同底数幂的乘法:am·an=am+n (a≠0,m,n为整数 )
(2)幂的乘方:(am)n=amn (a≠0,m,n为整数 )
(3)积的乘方:(ab)n=anbn (a,b≠0 ,m,n为整数 )
同底数幂的除法:am÷an=am-n (a≠0,m,n为整数 )
分式的乘方: ( b≠0,m,n为整数 )
点拨运用二 (2分钟)
自学检测二(5分钟)
1、计算:
解:原式
解:原式
运算过程中可以采用负指数的形式,但是最终结果要表示成正指数的形式。
课堂小结(1分钟)
一、负整数指数幂的意义:
当n是正整数时,a-n= (a≠0)
二、整数指数幂的运算性质:
(1) am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
1.(益阳·中考)下列计算正确的是( )
A.30=0 B.-|-3|=-3
C.3-1=-3 D. =±3
2.(聊城·中考)下列计算不正确的是( )
A. B.
C. D.
当堂训练(15分钟)
B
B
3.(怀化·中考)若0A.x-1C.x2C
取特殊值
选做题
一艘轮船顺水航行n千米用了m小时,如果逆流航速是顺流的 ,那么这艘船逆流航行t 小时,走了多少路程?(课本P147第10题)
板书设计
一、负整数指数幂的运算性质:
当n是正整数时,a-n= (a≠0)
二、归纳整数指数幂的运算性质:
(1) am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
已学整数指数幂有以下运算性质:
(6) 0指数幂的运算:当a≠0时,a0=1
(1)同底数幂的乘法:am·an=am+n (a≠0 m、n为正整数)
(2)幂的乘方:(am)n=amn (a≠0 m、n为正整数)
(3)积的乘方:(ab)n=anbn (a,b≠0 m、n为正整数)
(4)同底数幂的除法:am÷an=am-n (a≠0 m、n为正整数且m>n)
(5)分式的乘方: ( b≠0 ,n是正整数)
那指数幂能否是负整数呢?能的话,那运算性质有什么变化吗?
复习回顾
学习目标(1分钟)
1、理解负整数指数幂的意义
2、掌握整数指数幂的运算性质
3、会运用这一性质进行简单的计算
自学指导一 (5分钟)
阅读教材143页上半部分,思考并回答以下问题:
am÷an=am-n (a≠0, m、n为正整数且m>n)
a5÷a3=a2
a3÷a5=?
a3÷a5=
(a≠0)
也就是说,a-n是an的 .
1、去掉上述法则的适用条件,用上述运算性质可得:
a-2
2、用分式约分可得:
a3÷a5=
3、得出的两结果是什么关系 :
4、你能得到什么结论 :
倒数
点拨运用一 (2分钟)
温馨提示:
公式里面的a可以是不等于0的任何数字或式子。
(a≠0)
也就是说,a-n是an的倒数
1、填空:
9
16
自学检测一(10分钟)
2、利用负整指数幂把下列各式化成不含分母的式子
1、
2、
阅读课本143页如下特例思考:
引入负整数指数和0指数后,m,n 是任意整数是否适用于运算性质 ?
自学指导二 (5分钟)
am·an=am+n (a≠0,m,n是整数 )
am·an=am+n (a≠0 m、n为正整数)
自此指数的取值范围推广到全体整数,这样,整数指数的运算性质可重新归纳为三大类:
(1)同底数幂的乘法:am·an=am+n (a≠0,m,n为整数 )
(2)幂的乘方:(am)n=amn (a≠0,m,n为整数 )
(3)积的乘方:(ab)n=anbn (a,b≠0 ,m,n为整数 )
同底数幂的除法:am÷an=am-n (a≠0,m,n为整数 )
分式的乘方: ( b≠0,m,n为整数 )
点拨运用二 (2分钟)
自学检测二(5分钟)
1、计算:
解:原式
解:原式
运算过程中可以采用负指数的形式,但是最终结果要表示成正指数的形式。
课堂小结(1分钟)
一、负整数指数幂的意义:
当n是正整数时,a-n= (a≠0)
二、整数指数幂的运算性质:
(1) am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
1.(益阳·中考)下列计算正确的是( )
A.30=0 B.-|-3|=-3
C.3-1=-3 D. =±3
2.(聊城·中考)下列计算不正确的是( )
A. B.
C. D.
当堂训练(15分钟)
B
B
3.(怀化·中考)若0
取特殊值
选做题
一艘轮船顺水航行n千米用了m小时,如果逆流航速是顺流的 ,那么这艘船逆流航行t 小时,走了多少路程?(课本P147第10题)
板书设计
一、负整数指数幂的运算性质:
当n是正整数时,a-n= (a≠0)
二、归纳整数指数幂的运算性质:
(1) am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
