第20章 数据的初步分析单元达标检测卷(含答案)
文档属性
| 名称 | 第20章 数据的初步分析单元达标检测卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 11:02:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第20章
达标检测卷
一、选择题(每题3分,共30分)
1.已知一个样本中,50个数据分别落在五个组内,第一、二、三、五组数据的个数分别为2,8,15,5,则第四组的频率为( )
A.0.1
B.0.2
C.0.3
D.0.4
2.一个容量为60的样本中数据的最大值是187,最小值是140,取组距为6,则可以分成( )
A.7组
B.7组
C.8组
D.10组
3.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的鞋销售量如下表:
尺码/厘米
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
鞋店老板比较关注哪种尺码的鞋最畅销,也就是关注卖出鞋的尺码组成一组数据的( )
A.平均数
B.中位数
C.众数
D.方差
4.某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占40%,期末考试成绩占60%,小海同学这个学期的期中、期末成绩(百分制)分别是80分、90分,则小海这个学期的体育综合成绩是( )
A.88.5分
B.86分
C.87分
D.87.5分
5.某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度在8≤x<32这个范围的频率为( )
棉花纤维长度x
0≤x<8
8≤x<16
16≤x<24
24≤x<32
32≤x<40
频数
1
2
8
6
3
A.0.8
B.0.7
C.0.4
D.0.2
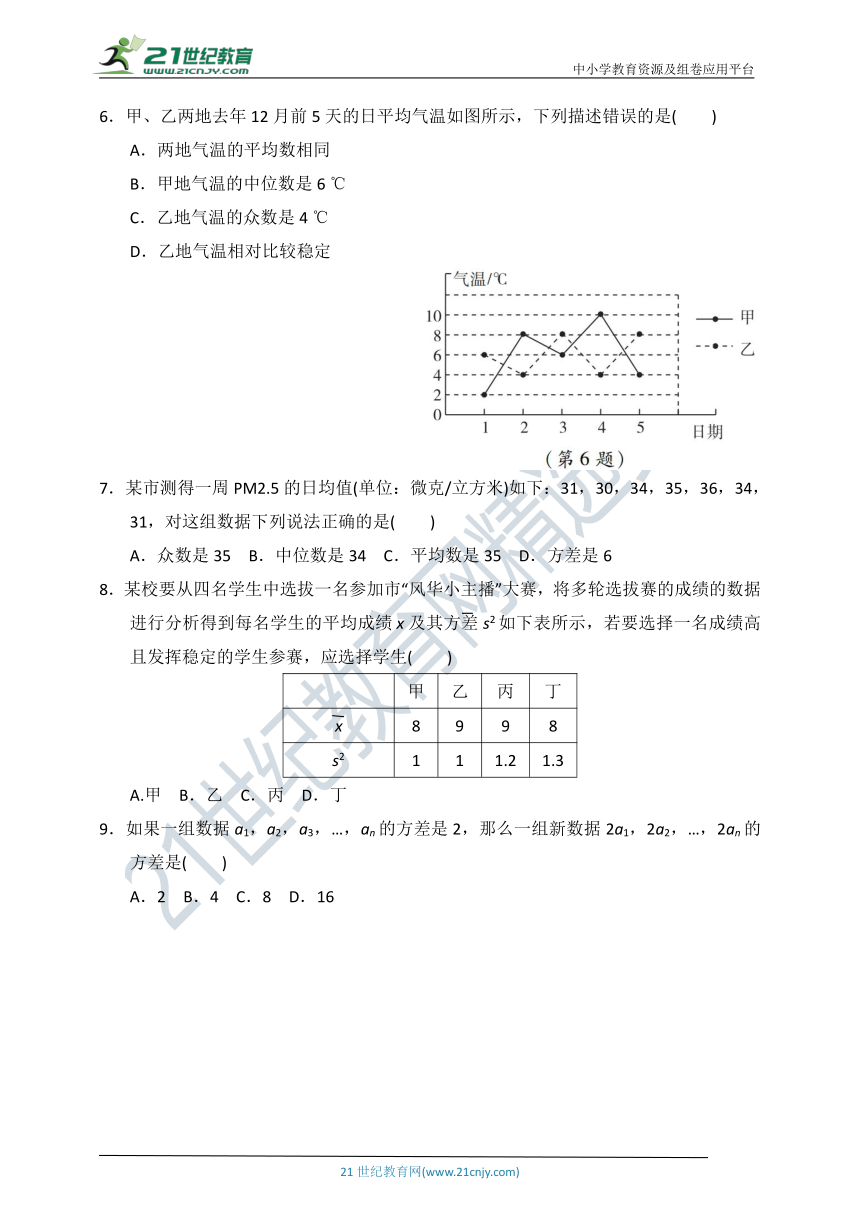
6.甲、乙两地去年12月前5天的日平均气温如图所示,下列描述错误的是( )
A.两地气温的平均数相同
B.甲地气温的中位数是6
℃
C.乙地气温的众数是4
℃
D.乙地气温相对比较稳定
7.某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
A.众数是35
B.中位数是34
C.平均数是35
D.方差是6
8.某校要从四名学生中选拔一名参加市“风华小主播”大赛,将多轮选拔赛的成绩的数据进行分析得到每名学生的平均成绩x及其方差s2如下表所示,若要选择一名成绩高且发挥稳定的学生参赛,应选择学生( )
甲
乙
丙
丁
x
8
9
9
8
s2
1
1
1.2
1.3
A.甲
B.乙
C.丙
D.丁
9.如果一组数据a1,a2,a3,…,an的方差是2,那么一组新数据2a1,2a2,…,2an的方差是( )
A.2
B.4
C.8
D.16
10.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级
参赛人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
某同学分析上表后得出如下结论:
①甲、乙两班学生汉字输入的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的个数不少于150为优秀);③甲班成绩的波动比乙班大.上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③
二、填空题(每题3分,共18分)
11.一组数据2,x,4,3,3的平均数是3,则这组数据的中位数是________.
12.下表是某中学男子篮球队队员的年龄统计表,他们的平均年龄是________岁.
年龄/岁
13
14
15
16
人数
1
5
5
1
13.某班47名学生的年龄统计结果如下表所示:
年龄/岁
13
14
15
16
人数
2
23
21
1
则这个班级的学生年龄的众数为________岁.
14.需要对一批排球的质量是否符合标准进行检测,其中质量超过标准的克数记为正数,不足标准的克数记为负数.现抽取8个排球,通过检测所得数据如下(单位:克):+1,-2,+1,0,+2,-3,0,+1,则这组数据的方差是________.
15.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为________.
16.某校举办以“保护环境,治理雾霾,从我做起”为主题的演讲比赛,现将所有比赛成绩(得分取整数,满分为100分)进行整理后分为5组,并绘制成如图所示的频数直方图.根据频数直方图提供的信息,下列结论:①参加比赛的学生共有52人;②比赛成绩为65分的学生有12人;③比赛成绩的中位数落在70.5分~80.5分这个分数段;④若比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率约为30.8%.正确的是________.(把所有正确结论的序号都填在横线上)
三、解答题(17~20题每题8分,其余每题10分,共52分)
17.某学校招聘教师,王明、李红和张丽参加了考试,评委从三个方面对他们进行打分,结果如下表所示(各项的满分为30分),最后总分的计算按课堂教学效果的分数?教学理念的分数?教材处理能力的分数=5:2:3的比例计算.如果你是该学校的教学校长,你会录用哪一位应聘者?试说明理由.
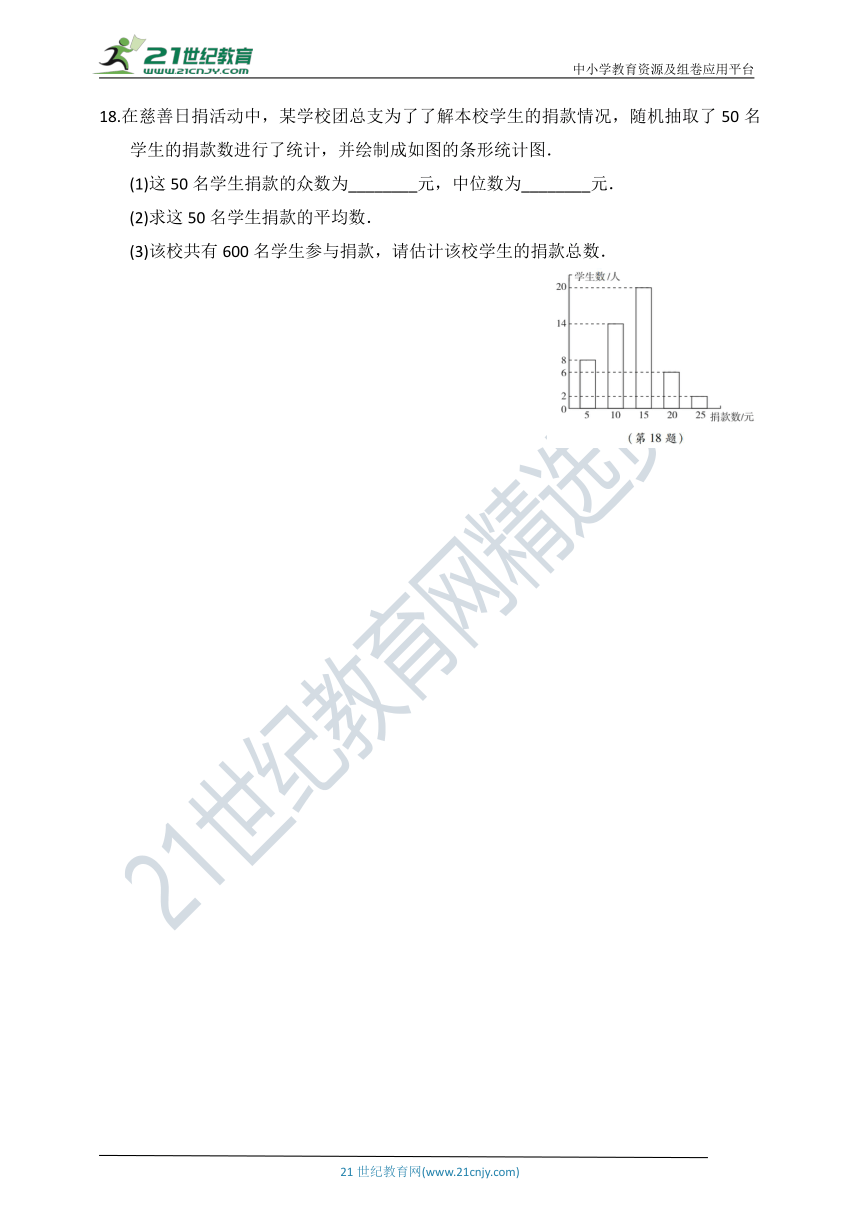
18.在慈善日捐活动中,某学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成如图的条形统计图.
(1)这50名学生捐款的众数为________元,中位数为________元.
(2)求这50名学生捐款的平均数.
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
19.某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对她所任教的八年级(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表(单位:分):
班级
平均数
中位数
众数
(1)班
24
24
(2)班
24
(2)若把24分以上(含24分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀?
(3)观察图中的数据分布情况,你认为哪个班的学生纠错的整体情况更好一些?
20.在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击7次,命中的环数如下表所示.
序号
1
2
3
4
5
6
7
甲命中的环数/环
7
8
8
6
9
8
10
乙命中的环数/环
5
10
6
7
8
10
10
根据以上信息,解决以下问题:
(1)写出甲、乙两人命中环数的众数;
(2)已知通过计算器求得x甲=8环,s2甲≈1.43,试比较甲、乙两人谁的成绩更稳定.
21.已知一组数据x1,x2,…,x6的平均数为1,方差为.
(1)求x21+x22+…+x26的值;
(2)若在这组数据中加入另1个数据x7,重新计算,平均数无变化,求这7个数据的方差.(结果用分数表示)
22.我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图如图所示,成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别
平均分/分
中位数/分
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队的成绩比八年级队好,但也有人说八年级队的成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
答案
一、1.D 2.C 3.C 4.B 5.A 6.C
7.B 8.B 9.C 10.A
二、11.3 12.14.5 13.14
14.2.5 点拨:∵x=×(+1-2+1+0+2-3+0+1)=0,
∴s2=×[(1-0)2+(-2-0)2+(1-0)2+(0-0)2+(2-0)2+(-3-0)2+(0-0)2+(1-0)2]=2.5.
15.6 点拨:由题意得
解得
∴这组新数据是3,4,5,6,8,8,8,其中位数是6.
16.①③④ 点拨:由题中的频数直方图可知,参加比赛的学生共有4+12+20+10+6=52(人),①正确;由已知条件和频数直方图得不出比赛成绩为65分的学生人数,②错误;将比赛成绩按从小到大的顺序排列,第26个,27个数据都在70.5分~80.5分这个分数段内,故比赛成绩的中位数落在70.5分~80.5分这个分数段,③正确;若比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率为×100%≈30.8%,④正确.
三、17.解:王明的成绩为
=24.3(分),
李红的成绩为=25.6(分),
张丽的成绩为=25(分).
∵25.6>25>24.3,∴李红将被录用.
18.解:(1)15;15
(2)这50名学生捐款的平均数为×(8×5+14×10+20×15+6×20+2×25)=13(元).
(3)估计该校学生的捐款总数为600×13=7
800(元).
19.解:(1)补全表格如下(单位:分):
班级
平均数
中位数
众数
(1)班
24
24
24
(2)班
24
24
21
(2)估计(1)班成绩优秀的学生有60×=42(名),估计(2)班成绩优秀的学生有60×=36(名).
答:估计(1)班有42名学生成绩优秀,(2)班有36名学生成绩优秀.
(3)(1)班的学生纠错的整体情况更好一些.
20.解:(1)由题意可知甲命中环数的众数为8环,乙命中环数的众数为10环.
(2)乙命中环数的平均数为x乙=
=8(环),乙命中环数的方差为s2乙=×[(5-8)2+(10-8)2+…+(10-8)2]=≈3.71.
∵x甲=8,s2甲≈1.43,
∴甲、乙的平均成绩一样,而甲的方差小于乙的方差,
∴甲的成绩更稳定.
21.解:(1)∵数据x1,x2,…,x6的平均数为1,
∴x1+x2+…+x6=1×6=6.
又∵方差为,
∴[(x1-1)2+(x2-1)2+…+(x6-1)2]=[x21+x22+…+x26-2(x1+x2+…+x6)+6]=(x21+x22+…+x26-2×6+6)=(x21+x22+…+x26)-1=,
∴x21+x22+…+x26=16.
(2)∵数据x1,x2,…,x7的平均数为1,∴x1+x2+…+x7=1×7=7.
∵x1+x2+…+x6=6,∴x7=1.
∵[(x1-1)2+(x2-1)2+…+(x6-1)2]=,
∴(x1-1)2+(x2-1)2+…+(x6-1)2=10,
∴[(x1-1)2+(x2-1)2+…+(x7-1)2]=[10+(1-1)2]=,即这7个数据的方差为.
22.解:(1)依题意得
解得
(2)m=6,n=20%.
(3)(答案不唯一)①八年级队的平均分高于七年级队;②八年级队的成绩比七年级队稳定.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第20章
达标检测卷
一、选择题(每题3分,共30分)
1.已知一个样本中,50个数据分别落在五个组内,第一、二、三、五组数据的个数分别为2,8,15,5,则第四组的频率为( )
A.0.1
B.0.2
C.0.3
D.0.4
2.一个容量为60的样本中数据的最大值是187,最小值是140,取组距为6,则可以分成( )
A.7组
B.7组
C.8组
D.10组
3.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的鞋销售量如下表:
尺码/厘米
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
鞋店老板比较关注哪种尺码的鞋最畅销,也就是关注卖出鞋的尺码组成一组数据的( )
A.平均数
B.中位数
C.众数
D.方差
4.某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占40%,期末考试成绩占60%,小海同学这个学期的期中、期末成绩(百分制)分别是80分、90分,则小海这个学期的体育综合成绩是( )
A.88.5分
B.86分
C.87分
D.87.5分
5.某棉纺厂为了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表所示,则棉花纤维长度在8≤x<32这个范围的频率为( )
棉花纤维长度x
0≤x<8
8≤x<16
16≤x<24
24≤x<32
32≤x<40
频数
1
2
8
6
3
A.0.8
B.0.7
C.0.4
D.0.2
6.甲、乙两地去年12月前5天的日平均气温如图所示,下列描述错误的是( )
A.两地气温的平均数相同
B.甲地气温的中位数是6
℃
C.乙地气温的众数是4
℃
D.乙地气温相对比较稳定
7.某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
A.众数是35
B.中位数是34
C.平均数是35
D.方差是6
8.某校要从四名学生中选拔一名参加市“风华小主播”大赛,将多轮选拔赛的成绩的数据进行分析得到每名学生的平均成绩x及其方差s2如下表所示,若要选择一名成绩高且发挥稳定的学生参赛,应选择学生( )
甲
乙
丙
丁
x
8
9
9
8
s2
1
1
1.2
1.3
A.甲
B.乙
C.丙
D.丁
9.如果一组数据a1,a2,a3,…,an的方差是2,那么一组新数据2a1,2a2,…,2an的方差是( )
A.2
B.4
C.8
D.16
10.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级
参赛人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
某同学分析上表后得出如下结论:
①甲、乙两班学生汉字输入的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字的个数不少于150为优秀);③甲班成绩的波动比乙班大.上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③
二、填空题(每题3分,共18分)
11.一组数据2,x,4,3,3的平均数是3,则这组数据的中位数是________.
12.下表是某中学男子篮球队队员的年龄统计表,他们的平均年龄是________岁.
年龄/岁
13
14
15
16
人数
1
5
5
1
13.某班47名学生的年龄统计结果如下表所示:
年龄/岁
13
14
15
16
人数
2
23
21
1
则这个班级的学生年龄的众数为________岁.
14.需要对一批排球的质量是否符合标准进行检测,其中质量超过标准的克数记为正数,不足标准的克数记为负数.现抽取8个排球,通过检测所得数据如下(单位:克):+1,-2,+1,0,+2,-3,0,+1,则这组数据的方差是________.
15.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数为________.
16.某校举办以“保护环境,治理雾霾,从我做起”为主题的演讲比赛,现将所有比赛成绩(得分取整数,满分为100分)进行整理后分为5组,并绘制成如图所示的频数直方图.根据频数直方图提供的信息,下列结论:①参加比赛的学生共有52人;②比赛成绩为65分的学生有12人;③比赛成绩的中位数落在70.5分~80.5分这个分数段;④若比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率约为30.8%.正确的是________.(把所有正确结论的序号都填在横线上)
三、解答题(17~20题每题8分,其余每题10分,共52分)
17.某学校招聘教师,王明、李红和张丽参加了考试,评委从三个方面对他们进行打分,结果如下表所示(各项的满分为30分),最后总分的计算按课堂教学效果的分数?教学理念的分数?教材处理能力的分数=5:2:3的比例计算.如果你是该学校的教学校长,你会录用哪一位应聘者?试说明理由.
18.在慈善日捐活动中,某学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成如图的条形统计图.
(1)这50名学生捐款的众数为________元,中位数为________元.
(2)求这50名学生捐款的平均数.
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
19.某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对她所任教的八年级(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表(单位:分):
班级
平均数
中位数
众数
(1)班
24
24
(2)班
24
(2)若把24分以上(含24分)记为“优秀”,两班各有60名学生,请估计两班各有多少名学生成绩优秀?
(3)观察图中的数据分布情况,你认为哪个班的学生纠错的整体情况更好一些?
20.在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击7次,命中的环数如下表所示.
序号
1
2
3
4
5
6
7
甲命中的环数/环
7
8
8
6
9
8
10
乙命中的环数/环
5
10
6
7
8
10
10
根据以上信息,解决以下问题:
(1)写出甲、乙两人命中环数的众数;
(2)已知通过计算器求得x甲=8环,s2甲≈1.43,试比较甲、乙两人谁的成绩更稳定.
21.已知一组数据x1,x2,…,x6的平均数为1,方差为.
(1)求x21+x22+…+x26的值;
(2)若在这组数据中加入另1个数据x7,重新计算,平均数无变化,求这7个数据的方差.(结果用分数表示)
22.我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图如图所示,成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别
平均分/分
中位数/分
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队的成绩比八年级队好,但也有人说八年级队的成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
答案
一、1.D 2.C 3.C 4.B 5.A 6.C
7.B 8.B 9.C 10.A
二、11.3 12.14.5 13.14
14.2.5 点拨:∵x=×(+1-2+1+0+2-3+0+1)=0,
∴s2=×[(1-0)2+(-2-0)2+(1-0)2+(0-0)2+(2-0)2+(-3-0)2+(0-0)2+(1-0)2]=2.5.
15.6 点拨:由题意得
解得
∴这组新数据是3,4,5,6,8,8,8,其中位数是6.
16.①③④ 点拨:由题中的频数直方图可知,参加比赛的学生共有4+12+20+10+6=52(人),①正确;由已知条件和频数直方图得不出比赛成绩为65分的学生人数,②错误;将比赛成绩按从小到大的顺序排列,第26个,27个数据都在70.5分~80.5分这个分数段内,故比赛成绩的中位数落在70.5分~80.5分这个分数段,③正确;若比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率为×100%≈30.8%,④正确.
三、17.解:王明的成绩为
=24.3(分),
李红的成绩为=25.6(分),
张丽的成绩为=25(分).
∵25.6>25>24.3,∴李红将被录用.
18.解:(1)15;15
(2)这50名学生捐款的平均数为×(8×5+14×10+20×15+6×20+2×25)=13(元).
(3)估计该校学生的捐款总数为600×13=7
800(元).
19.解:(1)补全表格如下(单位:分):
班级
平均数
中位数
众数
(1)班
24
24
24
(2)班
24
24
21
(2)估计(1)班成绩优秀的学生有60×=42(名),估计(2)班成绩优秀的学生有60×=36(名).
答:估计(1)班有42名学生成绩优秀,(2)班有36名学生成绩优秀.
(3)(1)班的学生纠错的整体情况更好一些.
20.解:(1)由题意可知甲命中环数的众数为8环,乙命中环数的众数为10环.
(2)乙命中环数的平均数为x乙=
=8(环),乙命中环数的方差为s2乙=×[(5-8)2+(10-8)2+…+(10-8)2]=≈3.71.
∵x甲=8,s2甲≈1.43,
∴甲、乙的平均成绩一样,而甲的方差小于乙的方差,
∴甲的成绩更稳定.
21.解:(1)∵数据x1,x2,…,x6的平均数为1,
∴x1+x2+…+x6=1×6=6.
又∵方差为,
∴[(x1-1)2+(x2-1)2+…+(x6-1)2]=[x21+x22+…+x26-2(x1+x2+…+x6)+6]=(x21+x22+…+x26-2×6+6)=(x21+x22+…+x26)-1=,
∴x21+x22+…+x26=16.
(2)∵数据x1,x2,…,x7的平均数为1,∴x1+x2+…+x7=1×7=7.
∵x1+x2+…+x6=6,∴x7=1.
∵[(x1-1)2+(x2-1)2+…+(x6-1)2]=,
∴(x1-1)2+(x2-1)2+…+(x6-1)2=10,
∴[(x1-1)2+(x2-1)2+…+(x7-1)2]=[10+(1-1)2]=,即这7个数据的方差为.
22.解:(1)依题意得
解得
(2)m=6,n=20%.
(3)(答案不唯一)①八年级队的平均分高于七年级队;②八年级队的成绩比七年级队稳定.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
