华东师大版八年级上册数学学案:13.2.5三角形全等的判定(无答案)
文档属性
| 名称 | 华东师大版八年级上册数学学案:13.2.5三角形全等的判定(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 36.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 00:00:00 | ||
图片预览


文档简介
课题:13.2.5三角形全等的判定(SSS)
[课标要求]:掌握运用“SSS”识别三角形全等的条件
[导学目标]:
1、知识与技能:知道三角形全等的性质和三角形全等的判定是两个相反的问题,领会三角形
全等判定的意义.
2、过程与方法:通过画图,经历探究过程,得出“只满足一个或两个条件的两个三角形不一定全等”,培养探究能力.
3、情感态度与价值观:会运用“SSS”证明三角形全等,为证明线段相等或角相等创造条件;
[导学核心点]
导学重点:探究“只满足一个或两个条件的两个三角形不一定全等”
导学难点:探究“只满足一个或两个条件的两个三角形不一定全等”
导学关键:会运用“SSS”证明三角形全等,为证明线段相等或角相等创造条件;
[导学课时]:
[导学方法]:两个全等的三角形、类比法。
[导学过程设计]
导
学
设
计
批注修改
一、创设问题情景
1.只给一个条件:(1)画出一条边为6cm
三角形
(2)
画出一个角为30度的三角形.小组交流所画的三角形全等吗?
2.给出两个条件画三角形时,有几种可能的情况?分别按照下面条件,用刻度尺或量角器画三角形,并和小组的同学比较一下,所画的图形全等吗?
①三角形的一个内角为60°,一条边为3
cm;
②
三角形的两个内角分别为30°和70°;
③
三角形的两条边分别为3
cm和5
cm
从1、2画图归纳:如果只知道两个三角形有一个或两个对应相等的部分(边或角),那么这两个三角形
.
若给出三个条件画三角形,你能说出有几种可能的情况吗
二、学生自主学习
已知一个三角形的三条边长分别为4cm、5cm、6cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
全等三角形的一个判定方法:
对应相等的两个三角形全等
(简称为“边边边”或“SSS”)
几何语言:已知:如图,
∴
三、学生合作探究
1.如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
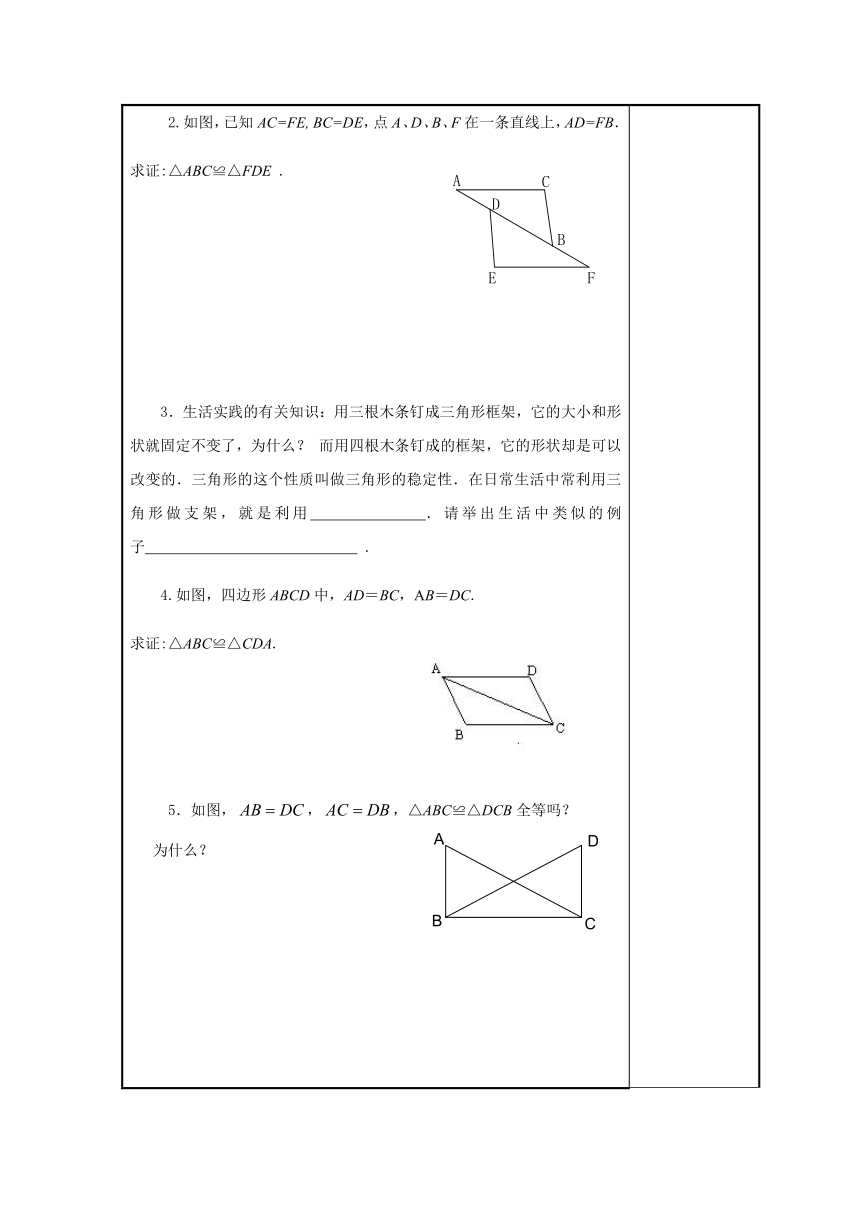
2.如图,已知AC=FE,
BC=DE,点A、D、B、F在一条直线上,AD=FB.
求证:△ABC≌△FDE
.
3.生活实践的有关知识:用三根木条钉成三角形框架,它的大小和形状就固定不变了,为什么?而用四根木条钉成的框架,它的形状却是可以改变的.三角形的这个性质叫做三角形的稳定性.在日常生活中常利用三角形做支架,就是利用
.请举出生活中类似的例子
.
4.如图,四边形ABCD中,AD=BC,AB=DC.
求证:△ABC≌△CDA.
5.如图,,,△ABC≌△DCB全等吗?
为什么?
6.完成下面的证明过程:如图,OA=OB,AC=BC.
求证:∠AOC=∠BOC.
证明:在△______和△_____中,
∴
≌
(SSS).
∴∠AOC=∠BOC(
).
四、知识方法小结
(1)知识方面:
(2)学习方法方面:
五、作业布置
《课后训练》
(一)填空题
1.如图,已知AC=DB,要使△ABC≌△DCB,还需知道的一个条件是________.
2.已知AC=FD,BC=ED,点B,D,C,E在一条直线上,要利用“SSS”,还需添加条件___________,得△ACB≌△_______.
3.如图△ABC中,AB=AC,现想利用证三角形全等证明∠B=∠C,若证三角形全等所用的公理是SSS公理,则图中所添加的辅助线应是_____________________.
4、填空完成下列求解过程:
????
如右图已知:AE=DE,EB=EC,AB=CD,
∠ACB=30°。
求:∠DBC
的度数
解:∵AE=DE,
=
(已知)
∴AE+EC=
+
(等式的性质)
即
=BD
在△ABC和△DBC中:
AB=
(
)
=BD(已证)
BC=
(
),
∴△
≌△
(
)
∴∠ACB
=∠
(全等三角形
相等)
∵∠ACB
=30°(
)
∴∠DBC
=
°(
)
板书设计
导学反思
1、本节亮点:
2、待改进处
[课标要求]:掌握运用“SSS”识别三角形全等的条件
[导学目标]:
1、知识与技能:知道三角形全等的性质和三角形全等的判定是两个相反的问题,领会三角形
全等判定的意义.
2、过程与方法:通过画图,经历探究过程,得出“只满足一个或两个条件的两个三角形不一定全等”,培养探究能力.
3、情感态度与价值观:会运用“SSS”证明三角形全等,为证明线段相等或角相等创造条件;
[导学核心点]
导学重点:探究“只满足一个或两个条件的两个三角形不一定全等”
导学难点:探究“只满足一个或两个条件的两个三角形不一定全等”
导学关键:会运用“SSS”证明三角形全等,为证明线段相等或角相等创造条件;
[导学课时]:
[导学方法]:两个全等的三角形、类比法。
[导学过程设计]
导
学
设
计
批注修改
一、创设问题情景
1.只给一个条件:(1)画出一条边为6cm
三角形
(2)
画出一个角为30度的三角形.小组交流所画的三角形全等吗?
2.给出两个条件画三角形时,有几种可能的情况?分别按照下面条件,用刻度尺或量角器画三角形,并和小组的同学比较一下,所画的图形全等吗?
①三角形的一个内角为60°,一条边为3
cm;
②
三角形的两个内角分别为30°和70°;
③
三角形的两条边分别为3
cm和5
cm
从1、2画图归纳:如果只知道两个三角形有一个或两个对应相等的部分(边或角),那么这两个三角形
.
若给出三个条件画三角形,你能说出有几种可能的情况吗
二、学生自主学习
已知一个三角形的三条边长分别为4cm、5cm、6cm.你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?
全等三角形的一个判定方法:
对应相等的两个三角形全等
(简称为“边边边”或“SSS”)
几何语言:已知:如图,
∴
三、学生合作探究
1.如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架.
求证:△ABD≌△ACD.
2.如图,已知AC=FE,
BC=DE,点A、D、B、F在一条直线上,AD=FB.
求证:△ABC≌△FDE
.
3.生活实践的有关知识:用三根木条钉成三角形框架,它的大小和形状就固定不变了,为什么?而用四根木条钉成的框架,它的形状却是可以改变的.三角形的这个性质叫做三角形的稳定性.在日常生活中常利用三角形做支架,就是利用
.请举出生活中类似的例子
.
4.如图,四边形ABCD中,AD=BC,AB=DC.
求证:△ABC≌△CDA.
5.如图,,,△ABC≌△DCB全等吗?
为什么?
6.完成下面的证明过程:如图,OA=OB,AC=BC.
求证:∠AOC=∠BOC.
证明:在△______和△_____中,
∴
≌
(SSS).
∴∠AOC=∠BOC(
).
四、知识方法小结
(1)知识方面:
(2)学习方法方面:
五、作业布置
《课后训练》
(一)填空题
1.如图,已知AC=DB,要使△ABC≌△DCB,还需知道的一个条件是________.
2.已知AC=FD,BC=ED,点B,D,C,E在一条直线上,要利用“SSS”,还需添加条件___________,得△ACB≌△_______.
3.如图△ABC中,AB=AC,现想利用证三角形全等证明∠B=∠C,若证三角形全等所用的公理是SSS公理,则图中所添加的辅助线应是_____________________.
4、填空完成下列求解过程:
????
如右图已知:AE=DE,EB=EC,AB=CD,
∠ACB=30°。
求:∠DBC
的度数
解:∵AE=DE,
=
(已知)
∴AE+EC=
+
(等式的性质)
即
=BD
在△ABC和△DBC中:
AB=
(
)
=BD(已证)
BC=
(
),
∴△
≌△
(
)
∴∠ACB
=∠
(全等三角形
相等)
∵∠ACB
=30°(
)
∴∠DBC
=
°(
)
板书设计
导学反思
1、本节亮点:
2、待改进处
