华东师大版八年级上册数学学案:13.2.6三角形全等的判定(HL)(无答案)
文档属性
| 名称 | 华东师大版八年级上册数学学案:13.2.6三角形全等的判定(HL)(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 40.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 23:06:37 | ||
图片预览

文档简介
课题:13.2.6三角形全等的判定(HL)
[课标要求]:
[导学目标]:
1、知识与技能:领会HL,会简单运用这一结论证明两个直角三角形全等.
2、过程与方法:探索HL定理的过程,体验用HL定理来解题的乐趣。
3、情感态度与价值观:会用HL定理来解题。
[导学核心点]
导学重点:运用HL解决相关的计算及证明等问题。
导学难点:
导学关键:会用HL来证明三角形全等及他们的应用。
[导学课时]:
[导学方法]:探索、归纳法。
[导学过程设计]
导
学
设
计
批注修改
一、创设问题情景
1.认真分析P73页“提出的问题”,情况回答。你的答案是:
_____________________________________________________________
_
________________________________________________________________2.
完成“做一做”,复述画图过程,写出“做一做”反映的规律:
____________________________________________________________
3.
仔细研读“例7”规范书写要求
________________________________________________________________
4.判断.
(1)判定直角三角形的全等的方法只有“HL”公理.
(2)有条边及第三边上的高对应相等的两个直角三角形全等.
(3)有一条直角边及斜边上的高对应相等的两个直角三角形全等.
(4)全等三角形对应边上的高相等.
其中正确的有:_______________________
5.使两个直角三角形全等的条件是
(
)
A.一个锐角对应相等;
B
两个锐角对应相等;
C
一条边对应相等
D
两条边对应相等.
二、学生自主学习
6.已知:如图,CD=BA,DF⊥BC,AE⊥BC,CE=BF.
求证:DF=AE.
证明:∵CE=BF,
∴____________.
∵DF⊥BC,AE⊥BC,
∴∠CFD__________________.
在Rt△CDF和Rt△BAE中,
____________
____________
∴Rt△______≌Rt△______(HL).
∴DF=AE.
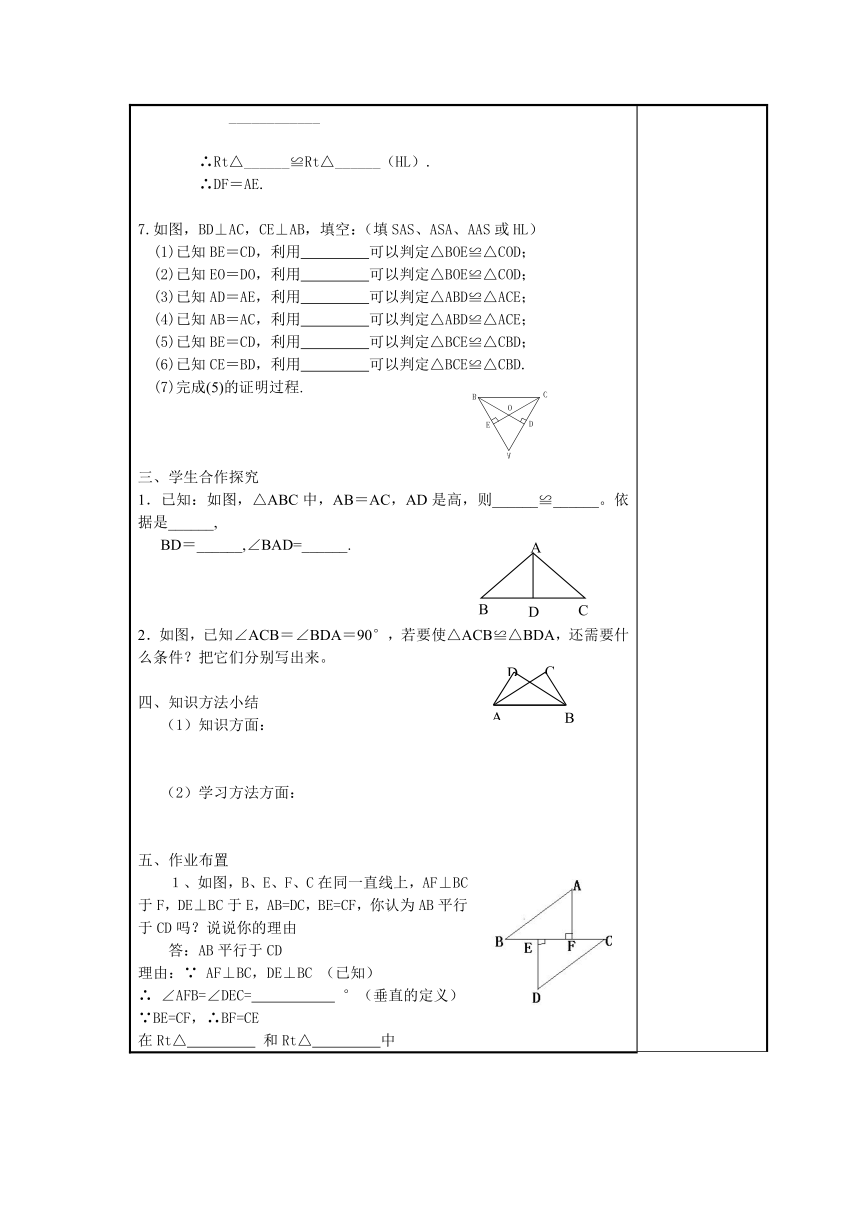
7.如图,BD⊥AC,CE⊥AB,填空:(填SAS、ASA、AAS或HL)
(1)已知BE=CD,利用
可以判定△BOE≌△COD;
(2)已知EO=DO,利用
可以判定△BOE≌△COD;
(3)已知AD=AE,利用
可以判定△ABD≌△ACE;
(4)已知AB=AC,利用
可以判定△ABD≌△ACE;
(5)已知BE=CD,利用
可以判定△BCE≌△CBD;
(6)已知CE=BD,利用
可以判定△BCE≌△CBD.
(7)完成(5)的证明过程.
三、学生合作探究
1.已知:如图,△ABC中,AB=AC,AD是高,则______≌______。依据是______,
BD=______,∠BAD=______.
2.如图,已知∠ACB=∠BDA=90°,若要使△ACB≌△BDA,还需要什么条件?把它们分别写出来。
四、知识方法小结
(1)知识方面:
(2)学习方法方面:
五、作业布置
1、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵
AF⊥BC,DE⊥BC
(已知)
∴
∠AFB=∠DEC=
°(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△
和Rt△
中
∵∴
≌
(
)
∴
=
(
)
∴
(内错角相等,两直线平行)
2、能力提升:(学有余力的同学完成)
如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
3、如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5)
若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
板书设计
导学反思
1、本节亮点:
2、待改进处
[课标要求]:
[导学目标]:
1、知识与技能:领会HL,会简单运用这一结论证明两个直角三角形全等.
2、过程与方法:探索HL定理的过程,体验用HL定理来解题的乐趣。
3、情感态度与价值观:会用HL定理来解题。
[导学核心点]
导学重点:运用HL解决相关的计算及证明等问题。
导学难点:
导学关键:会用HL来证明三角形全等及他们的应用。
[导学课时]:
[导学方法]:探索、归纳法。
[导学过程设计]
导
学
设
计
批注修改
一、创设问题情景
1.认真分析P73页“提出的问题”,情况回答。你的答案是:
_____________________________________________________________
_
________________________________________________________________2.
完成“做一做”,复述画图过程,写出“做一做”反映的规律:
____________________________________________________________
3.
仔细研读“例7”规范书写要求
________________________________________________________________
4.判断.
(1)判定直角三角形的全等的方法只有“HL”公理.
(2)有条边及第三边上的高对应相等的两个直角三角形全等.
(3)有一条直角边及斜边上的高对应相等的两个直角三角形全等.
(4)全等三角形对应边上的高相等.
其中正确的有:_______________________
5.使两个直角三角形全等的条件是
(
)
A.一个锐角对应相等;
B
两个锐角对应相等;
C
一条边对应相等
D
两条边对应相等.
二、学生自主学习
6.已知:如图,CD=BA,DF⊥BC,AE⊥BC,CE=BF.
求证:DF=AE.
证明:∵CE=BF,
∴____________.
∵DF⊥BC,AE⊥BC,
∴∠CFD__________________.
在Rt△CDF和Rt△BAE中,
____________
____________
∴Rt△______≌Rt△______(HL).
∴DF=AE.
7.如图,BD⊥AC,CE⊥AB,填空:(填SAS、ASA、AAS或HL)
(1)已知BE=CD,利用
可以判定△BOE≌△COD;
(2)已知EO=DO,利用
可以判定△BOE≌△COD;
(3)已知AD=AE,利用
可以判定△ABD≌△ACE;
(4)已知AB=AC,利用
可以判定△ABD≌△ACE;
(5)已知BE=CD,利用
可以判定△BCE≌△CBD;
(6)已知CE=BD,利用
可以判定△BCE≌△CBD.
(7)完成(5)的证明过程.
三、学生合作探究
1.已知:如图,△ABC中,AB=AC,AD是高,则______≌______。依据是______,
BD=______,∠BAD=______.
2.如图,已知∠ACB=∠BDA=90°,若要使△ACB≌△BDA,还需要什么条件?把它们分别写出来。
四、知识方法小结
(1)知识方面:
(2)学习方法方面:
五、作业布置
1、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵
AF⊥BC,DE⊥BC
(已知)
∴
∠AFB=∠DEC=
°(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△
和Rt△
中
∵∴
≌
(
)
∴
=
(
)
∴
(内错角相等,两直线平行)
2、能力提升:(学有余力的同学完成)
如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
3、如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5)
若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
板书设计
导学反思
1、本节亮点:
2、待改进处
