第14章 勾股定理解题的十种常见题型 课件(共33张PPT)
文档属性
| 名称 | 第14章 勾股定理解题的十种常见题型 课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 12:06:25 | ||
图片预览









文档简介
(共33张PPT)
勾股定理解题的十种常见题型
第14章
勾股定理
华东师大版
八年级数学上册
复习课件
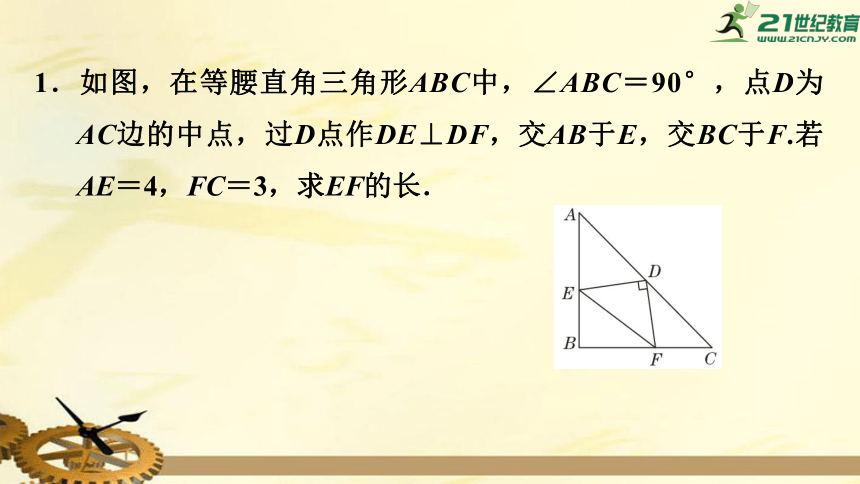
1.如图,在等腰直角三角形ABC中,∠ABC=90°,点D为AC边的中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=4,FC=3,求EF的长.
【点拨】当已知条件中有线段的平方关系时,
应选择用勾股定理说明.应用勾股定理说明两条线段相等的一般步骤:①找出图中说明结论所要用到的直角三角形;②根据勾股定理写出三边长的平方关系;③联系已知,等量代换,求之即可.
2.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2-CD2.求证:AB=BC.
(2)求证:BE2+CF2=EF2.
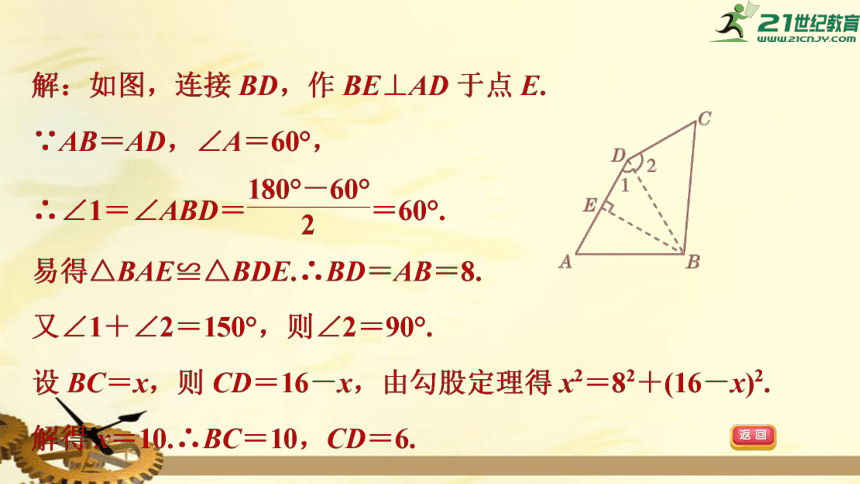
4.如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD的周长为32,求BC和CD的长度.
5.如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′处.若AB=6,BC=9,求BF的长.
6.如图,在Rt△ABC中,∠ACB=90°,AB=5
cm,AC=3
cm,动点P从点B出发沿射线BC以1
cm/s的速度移动,设运动的时间为t
s.
(1)求BC边的长;
解:在Rt△ABC中,BC2=AB2-AC2=52-32=16,∴BC=4
cm.
(2)当△ABP为直角三角形时,借助图①求t的值;
解:由题意知BP=t
cm,当△ABP为直角三角形时,有两种情况:
Ⅰ.如图①,当∠APB为直角时,点P与点C重合,BP=BC=4
cm,即t=4.
(3)当△ABP为等腰三角形时,借助图②求t的值.
解:当△ABP为等腰三角形时,有三种情况:
Ⅰ.如图①,当BP=AB时,t=5;
Ⅱ.如图②,当AB=AP时,BP=2BC=8
cm,即t=8;
7.如图,某学校(A点)到公路(直线l)的距离为300
m,到公交站(D点)的距离为500
m.现要在公路边上建一个商店(C点),使之到学校A及公交站D的距离相等,求商店C与公交站D之间的距离.
8.如图,小明家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60
m到达河边B处取水,然后沿另一方向走80
m到达菜地C处浇水,最后沿第三方向走100
m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
解:小明在河边B处取水后是沿南偏东60°方向行走的.理由如下:
由题易知AB=60
m,BC=80
m,AC=100
m,∴AB2+BC2=AC2.∴∠ABC=90°.
又∵AD∥NM,∴∠NBA=∠BAD=30°.
∴∠MBC=180°-90°-30°=60°.
∴小明在河边B处取水后是沿南偏东60°方向行走的.
9.【中考·绍兴】如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕
点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长;
解:AM=AD+DM=40或AM=AD-DM=20.
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1旋转到其内的点D2处,连接D1D2,如图②,此时∠AD2C=135°,CD2=60,求BD2的长.
解:如图,连接CD1.
10.如图,红星村A和幸福村B在河岸CD的同侧,它们到河岸CD的距离AC,BD分别为1千米和3千米,又知道CD的长为3千米,现要在河岸CD上建一水厂向两村输送自来水,铺设水管的工程费用为每千米20
000元.
(1)请在CD上选取水厂的位置,使铺设水管的费用最省;
(2)求铺设水管的最省总费用.
【点拨】在直线上找一点使其到直线同侧的两点的距离之和最短的方法:先找到其中一个点关于该直线的对称点,连接对称点与另一个点的线段与该直线的交点即为所找的点.
(1)请在CD上选取水厂的位置,使铺设水管的费用最省;
(2)求铺设水管的最省总费用.
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
勾股定理解题的十种常见题型
第14章
勾股定理
华东师大版
八年级数学上册
复习课件
1.如图,在等腰直角三角形ABC中,∠ABC=90°,点D为AC边的中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=4,FC=3,求EF的长.
【点拨】当已知条件中有线段的平方关系时,
应选择用勾股定理说明.应用勾股定理说明两条线段相等的一般步骤:①找出图中说明结论所要用到的直角三角形;②根据勾股定理写出三边长的平方关系;③联系已知,等量代换,求之即可.
2.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2-CD2.求证:AB=BC.
(2)求证:BE2+CF2=EF2.
4.如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形ABCD的周长为32,求BC和CD的长度.
5.如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′处.若AB=6,BC=9,求BF的长.
6.如图,在Rt△ABC中,∠ACB=90°,AB=5
cm,AC=3
cm,动点P从点B出发沿射线BC以1
cm/s的速度移动,设运动的时间为t
s.
(1)求BC边的长;
解:在Rt△ABC中,BC2=AB2-AC2=52-32=16,∴BC=4
cm.
(2)当△ABP为直角三角形时,借助图①求t的值;
解:由题意知BP=t
cm,当△ABP为直角三角形时,有两种情况:
Ⅰ.如图①,当∠APB为直角时,点P与点C重合,BP=BC=4
cm,即t=4.
(3)当△ABP为等腰三角形时,借助图②求t的值.
解:当△ABP为等腰三角形时,有三种情况:
Ⅰ.如图①,当BP=AB时,t=5;
Ⅱ.如图②,当AB=AP时,BP=2BC=8
cm,即t=8;
7.如图,某学校(A点)到公路(直线l)的距离为300
m,到公交站(D点)的距离为500
m.现要在公路边上建一个商店(C点),使之到学校A及公交站D的距离相等,求商店C与公交站D之间的距离.
8.如图,小明家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60
m到达河边B处取水,然后沿另一方向走80
m到达菜地C处浇水,最后沿第三方向走100
m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
解:小明在河边B处取水后是沿南偏东60°方向行走的.理由如下:
由题易知AB=60
m,BC=80
m,AC=100
m,∴AB2+BC2=AC2.∴∠ABC=90°.
又∵AD∥NM,∴∠NBA=∠BAD=30°.
∴∠MBC=180°-90°-30°=60°.
∴小明在河边B处取水后是沿南偏东60°方向行走的.
9.【中考·绍兴】如图①是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕
点D旋转,AD=30,DM=10.
(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长;
解:AM=AD+DM=40或AM=AD-DM=20.
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1旋转到其内的点D2处,连接D1D2,如图②,此时∠AD2C=135°,CD2=60,求BD2的长.
解:如图,连接CD1.
10.如图,红星村A和幸福村B在河岸CD的同侧,它们到河岸CD的距离AC,BD分别为1千米和3千米,又知道CD的长为3千米,现要在河岸CD上建一水厂向两村输送自来水,铺设水管的工程费用为每千米20
000元.
(1)请在CD上选取水厂的位置,使铺设水管的费用最省;
(2)求铺设水管的最省总费用.
【点拨】在直线上找一点使其到直线同侧的两点的距离之和最短的方法:先找到其中一个点关于该直线的对称点,连接对称点与另一个点的线段与该直线的交点即为所找的点.
(1)请在CD上选取水厂的位置,使铺设水管的费用最省;
(2)求铺设水管的最省总费用.
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
