苏科版八年级上册 第3章 勾股定理的常见题型复习教案
文档属性
| 名称 | 苏科版八年级上册 第3章 勾股定理的常见题型复习教案 |  | |
| 格式 | zip | ||
| 文件大小 | 70.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 07:05:16 | ||
图片预览


文档简介
教学内容
勾股定理的常考题型
教学目标
熟悉并掌握勾股定理的常见题型
重点
掌握常考题型
难点
勾股定理的应用
教学过程
专训1:利用勾股定理进行计算或证明
练习1:如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线交BC的延长线与点E,求CE的长
练习2:如图,在△ABC中,∠A=90°,点D是BC的中点,点E、F分别在AB、AC上,且∠EDF=90°,连接EF,求证:
专训2:利用勾股定理解决折叠问题
利用勾股定理解决有关图形折叠计算问题的一般思路:
(1)运用折叠的性质找出相等的线段或角;
(2)在图形中找到一个直角三角形,然后设图形中某一线段的长为x,将此直角三角形的三边长用数或含有x的代数式表示出来
(3)利用勾股定理列方程求出x
(4)进行相关计算解决问题
练习1:如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8
,将它的锐角A翻折,使得点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,求DE的值.
练习2:如图,矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色
若点P为EF边上的中点,试说明CP⊥EF的理由
求FG的长
求阴影部分的面积
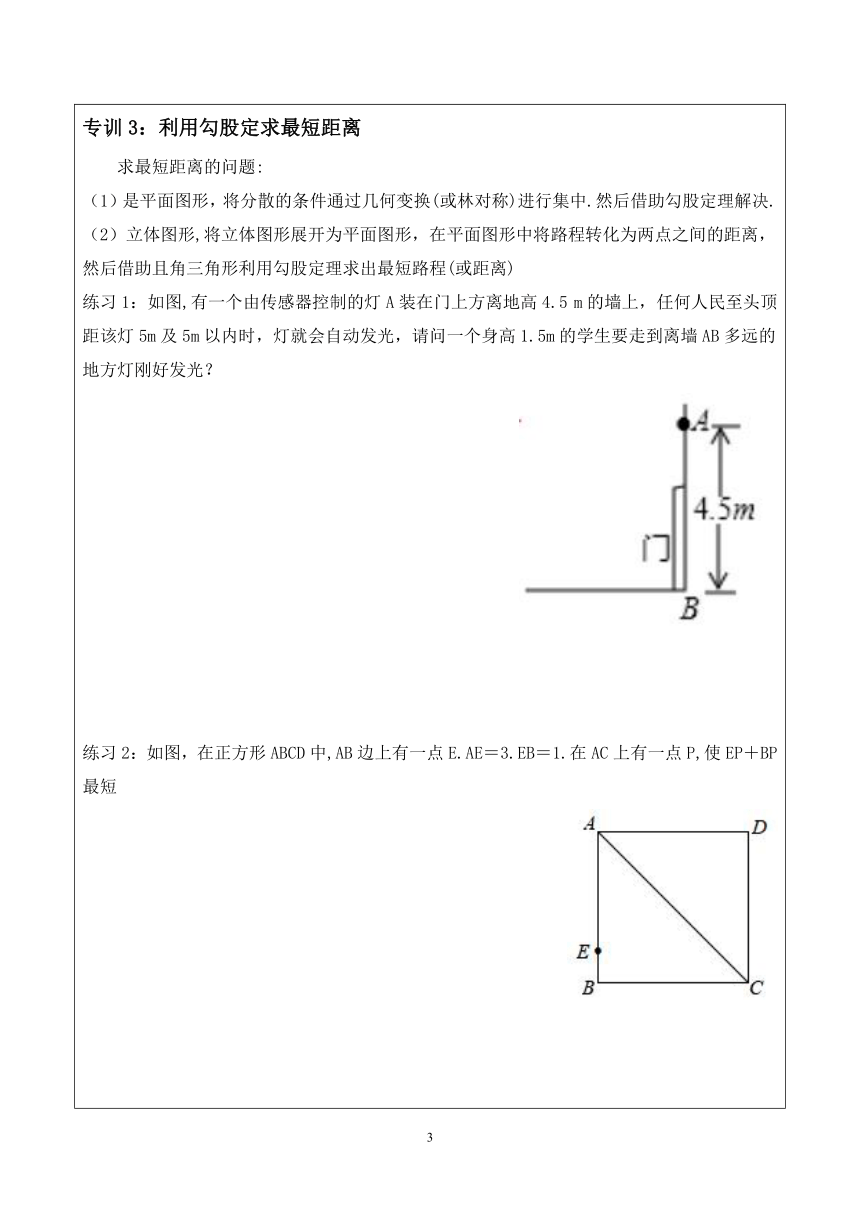
专训3:利用勾股定求最短距离
求最短距离的问题:
(1)是平面图形,将分散的条件通过几何变换(或林对称)进行集中.然后借助勾股定理解决.
(2)立体图形,将立体图形展开为平面图形,在平面图形中将路程转化为两点之间的距离,然后借助且角三角形利用勾股定理求出最短路程(或距离)
练习1:如图,有一个由传感器控制的灯A装在门上方离地高4.5
m的墙上,任何人民至头顶距该灯5m及5m以内时,灯就会自动发光,请问一个身高1.5m的学生要走到离墙AB多远的地方灯刚好发光?
练习2:如图,在正方形ABCD中,AB边上有一点E.AE=3.EB=1.在AC上有一点P,使EP+BP最短
练习3:有个长方体纸盒,如图所示,小明所在数学小组研究由长方体的底面A点到长方体中与A点相对的B点的面上的最短距离。若长方体的长为12,宽为9,高为5,请你帮助该小组求出在面上由A点到B点的最短距离.
(参考数据:21.592≈466
,18.442≈340,19.242≈370)
练习4:我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛滕自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看成一个圆柱,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点人处编绕而上,绕五周后其末端恰好到达点B处则葛藤的最短长度是
尺
练习5:请阅读下列材料
问题:如图1,圆柱的底面半径为1dm,BC是底面直径圆柱高AB为5
dm.求一只蚂蚁从点
A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线:
路线1:高线AB+底面直径BC,如图1所示
路线2:侧面展开图中的线段AC,如图2所示(结果保留π)
(1)设路线1的长度为,则
;设路线2的长度为,则
。
所以选择路线
(填1或2)较短
(2)小明把条件改成:“圆柱的底面半径为5
dm,高AB为1
dm”继续按上面的路线进行计算.此时,路线1:
;路线2:
;所以选择路线
(填1或2)较短
(3)请你帮小明继续研究:当圆柱的底面半径为2dm,高为hdm时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短?
专训4:勾股定理的实际应用
勾股定理及其逆定理揭示了直角三角形三边之间的数量关系,在实际生活中应用广泛,在解题时要注意将实际问题转化为直角三角形问题,利用勾股定理解决。
练习1:有一辆装满货物的卡车,高2.5米,宽1.6米,要开进如图所示的上边是半圆,下边是长方形的桥洞,已知半圆的直径为2米,长方形的另一条边长是2.3
米.
此辆卡车能否通过此桥洞?试说明你的理由
为了适应车流量的增加,相关部门想把桥洞改为双行道,并且要使宽1.2米,高2.8米的卡车能安全通过,那么此桥洞的宽至少应增加到多少米?
练习2:如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号两艘轮船同时离开港口。各自沿一固定方向航行,“远航”号以每小时16海里的速度向北偏东40°方向航行,“海天”号以每小时12海里的速度向北偏西一定的
角度的航向行驶,它们离港口一个半小时后分别位于Q、R处,且相距30海里(即RQ=30海里).解答下列问题.
求PR、PQ的值
求“海天”号航行的方向.
(即求北偏西多少度)
综合练习:
本章涉及的数学思想主要有两种:
(1)方程思想,就是设未知数利用勾股定理列方程求线段长。
(2)分类讨论思想。分类讨论主要有两种类型:
①一种是在直角三角形中给出两条边的长,未具体说明哪条边是斜边,需要分类讨论;
②另一种是给出三角形中两条边的长及第三边上的高,求第三边长时。这需要分类讨论.
练习1:在△ABC中,AB=30
,BC=28
,AC=26.求△ABC的面积.
某学习小组经过合作交流给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
(1)如图,作AD⊥BC于D,设BD=x,用含x的代数式表示CD
(2)根据勾股定理,把AD作为“桥梁”,建立方程模型
(3)利用勾股定理求出AD的长,再计算三角形的面积。
练习2:如图,五边形ABCDE是学校的一块种植基地示意图,这块基地可以分成正方形BCDE和直角三角形ABE。已知这个五边形的周长为88米正方形BCDE的面积为400平方米设AB=a米,AE=b米,BC=c米,求a、b、c的值分别为多少?
勾股定理的常考题型
教学目标
熟悉并掌握勾股定理的常见题型
重点
掌握常考题型
难点
勾股定理的应用
教学过程
专训1:利用勾股定理进行计算或证明
练习1:如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线交BC的延长线与点E,求CE的长
练习2:如图,在△ABC中,∠A=90°,点D是BC的中点,点E、F分别在AB、AC上,且∠EDF=90°,连接EF,求证:
专训2:利用勾股定理解决折叠问题
利用勾股定理解决有关图形折叠计算问题的一般思路:
(1)运用折叠的性质找出相等的线段或角;
(2)在图形中找到一个直角三角形,然后设图形中某一线段的长为x,将此直角三角形的三边长用数或含有x的代数式表示出来
(3)利用勾股定理列方程求出x
(4)进行相关计算解决问题
练习1:如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8
,将它的锐角A翻折,使得点A落在BC边的中点D处,折痕交AC边于点E,交AB边于点F,求DE的值.
练习2:如图,矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色
若点P为EF边上的中点,试说明CP⊥EF的理由
求FG的长
求阴影部分的面积
专训3:利用勾股定求最短距离
求最短距离的问题:
(1)是平面图形,将分散的条件通过几何变换(或林对称)进行集中.然后借助勾股定理解决.
(2)立体图形,将立体图形展开为平面图形,在平面图形中将路程转化为两点之间的距离,然后借助且角三角形利用勾股定理求出最短路程(或距离)
练习1:如图,有一个由传感器控制的灯A装在门上方离地高4.5
m的墙上,任何人民至头顶距该灯5m及5m以内时,灯就会自动发光,请问一个身高1.5m的学生要走到离墙AB多远的地方灯刚好发光?
练习2:如图,在正方形ABCD中,AB边上有一点E.AE=3.EB=1.在AC上有一点P,使EP+BP最短
练习3:有个长方体纸盒,如图所示,小明所在数学小组研究由长方体的底面A点到长方体中与A点相对的B点的面上的最短距离。若长方体的长为12,宽为9,高为5,请你帮助该小组求出在面上由A点到B点的最短距离.
(参考数据:21.592≈466
,18.442≈340,19.242≈370)
练习4:我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛滕自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看成一个圆柱,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点人处编绕而上,绕五周后其末端恰好到达点B处则葛藤的最短长度是
尺
练习5:请阅读下列材料
问题:如图1,圆柱的底面半径为1dm,BC是底面直径圆柱高AB为5
dm.求一只蚂蚁从点
A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线:
路线1:高线AB+底面直径BC,如图1所示
路线2:侧面展开图中的线段AC,如图2所示(结果保留π)
(1)设路线1的长度为,则
;设路线2的长度为,则
。
所以选择路线
(填1或2)较短
(2)小明把条件改成:“圆柱的底面半径为5
dm,高AB为1
dm”继续按上面的路线进行计算.此时,路线1:
;路线2:
;所以选择路线
(填1或2)较短
(3)请你帮小明继续研究:当圆柱的底面半径为2dm,高为hdm时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短?
专训4:勾股定理的实际应用
勾股定理及其逆定理揭示了直角三角形三边之间的数量关系,在实际生活中应用广泛,在解题时要注意将实际问题转化为直角三角形问题,利用勾股定理解决。
练习1:有一辆装满货物的卡车,高2.5米,宽1.6米,要开进如图所示的上边是半圆,下边是长方形的桥洞,已知半圆的直径为2米,长方形的另一条边长是2.3
米.
此辆卡车能否通过此桥洞?试说明你的理由
为了适应车流量的增加,相关部门想把桥洞改为双行道,并且要使宽1.2米,高2.8米的卡车能安全通过,那么此桥洞的宽至少应增加到多少米?
练习2:如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号两艘轮船同时离开港口。各自沿一固定方向航行,“远航”号以每小时16海里的速度向北偏东40°方向航行,“海天”号以每小时12海里的速度向北偏西一定的
角度的航向行驶,它们离港口一个半小时后分别位于Q、R处,且相距30海里(即RQ=30海里).解答下列问题.
求PR、PQ的值
求“海天”号航行的方向.
(即求北偏西多少度)
综合练习:
本章涉及的数学思想主要有两种:
(1)方程思想,就是设未知数利用勾股定理列方程求线段长。
(2)分类讨论思想。分类讨论主要有两种类型:
①一种是在直角三角形中给出两条边的长,未具体说明哪条边是斜边,需要分类讨论;
②另一种是给出三角形中两条边的长及第三边上的高,求第三边长时。这需要分类讨论.
练习1:在△ABC中,AB=30
,BC=28
,AC=26.求△ABC的面积.
某学习小组经过合作交流给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
(1)如图,作AD⊥BC于D,设BD=x,用含x的代数式表示CD
(2)根据勾股定理,把AD作为“桥梁”,建立方程模型
(3)利用勾股定理求出AD的长,再计算三角形的面积。
练习2:如图,五边形ABCDE是学校的一块种植基地示意图,这块基地可以分成正方形BCDE和直角三角形ABE。已知这个五边形的周长为88米正方形BCDE的面积为400平方米设AB=a米,AE=b米,BC=c米,求a、b、c的值分别为多少?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
