苏科版八年级数学上册 第三章 勾股定理 直角三角形的判定、赵爽弦图勾股数的拓展运用(无答案)
文档属性
| 名称 | 苏科版八年级数学上册 第三章 勾股定理 直角三角形的判定、赵爽弦图勾股数的拓展运用(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 442.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 07:08:06 | ||
图片预览


文档简介
勾:直角三角形较短的直角边;股:直角三角形较长的直角边;弦:斜边。
1、勾股定理:
直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2。
2、勾股定理的逆定理:
如果三角形的三边长a,b,c有关系a2+b2=c2,那么这个三角形是直角三角形。
3、勾股数:
满足a2+b2=c2的三个正整数,称为勾股数。
若是勾股数组,则na、nb、nc也是勾股数组。
4、简单运用:
⑴勾股定理——常用于求边长、周长、面积;
理解:①已知直角三角形的两边求第三边,并能求出周长、面积。
②用于证明线段平方关系的问题。
③利用勾股定理,作出长为的线段
⑵勾股定理的逆定理——常用于判断三角形的形状;
理解:①确定最大边(不妨设为c);?
②若c2=a2+b2,则△ABC是以∠C为直角的三角形;?
若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);
?
若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)
考点1:直角三角形的判断
例1下列四组线段中,可以构成直角三角形的是(
▲
)
A.5,6,7
B.0.7,2.4,2.5
C.1,1,2
D.1,,3
例2.
下列各数组中,不是勾股数组的是(
▲
)
A.5,12,13
B.9,40,
41
C.8,12,15
D.3,4,5
例3
下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是(
)
A.5cm,12cm,13cm
B.1cm,1
cm,cm
C.1cm,2
cm,
cm
D.cm,2cm,
cm
例4判断由线段a、b、c组成的三角形是不是直角三角形.
(1)a=,b=1,c=;
(2)a=40
,b=50,c=60;
(3)a=35,b=12,c=37
例5
满足下列条件的三角形中,不是直角三角形的是(
)
A.三内角之比为1∶2∶3
B.三边长的平方之比为1∶2∶3
C.三边长之比为3∶4∶5
D.三内角之比为3∶4∶5
例6.下列给出的三条线段的长,能组成直角三角形的是
A.
1、2、3
B.
2、3、4
C.、、
D.
5、12、13
例7下列三角形中,可以构成直角三角形的有
A.三边长分别为2,2,3
B.三边长分别为3,3,5
C.三边长分别为4,5,6
D.三边长分别为1.5,2,2.5
例8
下列各组数中,不能构成直角三角形的一组是(
)
A.1,2,
B.1,2,
C.3,4,5
D.
6,8,12
考点2:勾股定理的证明
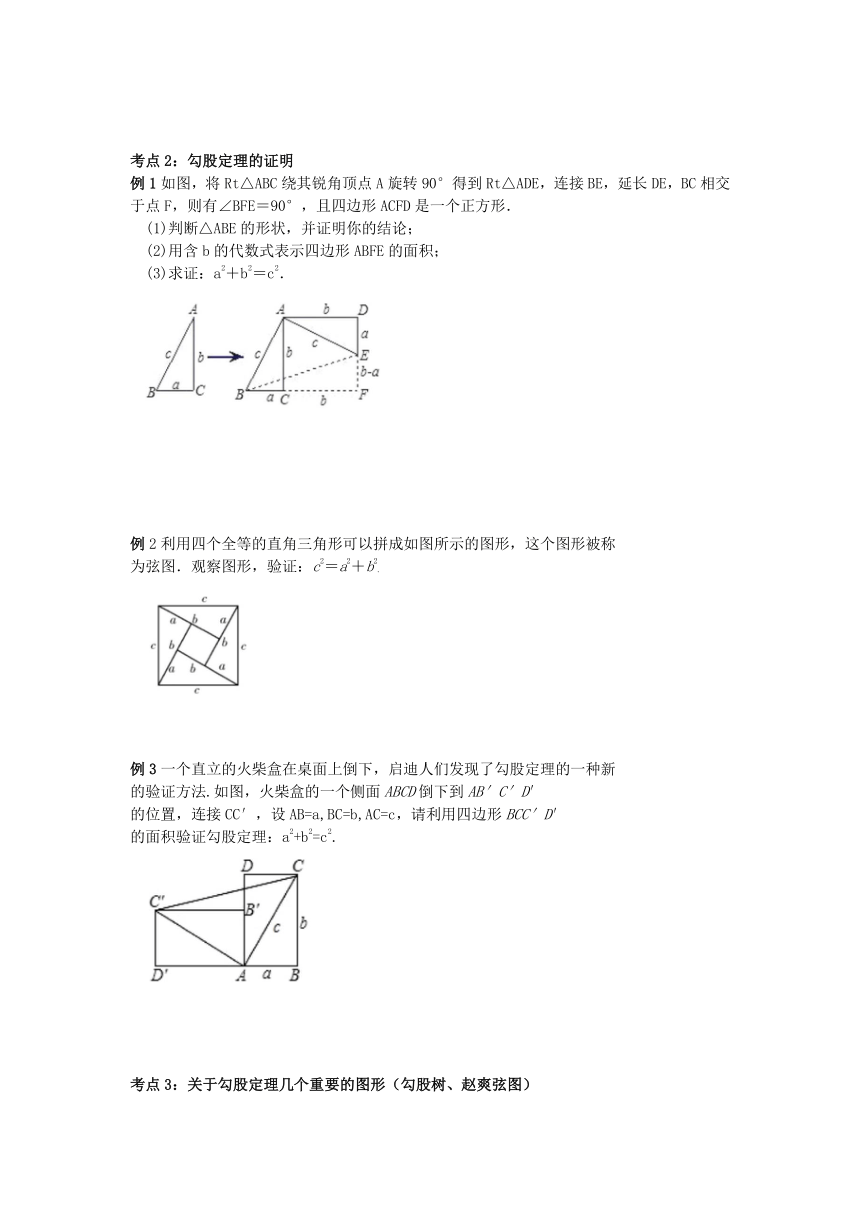
例1如图,将Rt△ABC绕其锐角顶点A旋转90°得到Rt△ADE,连接BE,延长DE,BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.
(1)判断△ABE的形状,并证明你的结论;
(2)用含b的代数式表示四边形ABFE的面积;
(3)求证:a2+b2=c2.
例2利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称
为弦图.观察图形,验证:c2=a2+b2.
例3一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新
的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′
的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′
的面积验证勾股定理:a2+b2=c2.
考点3:关于勾股定理几个重要的图形(勾股树、赵爽弦图)
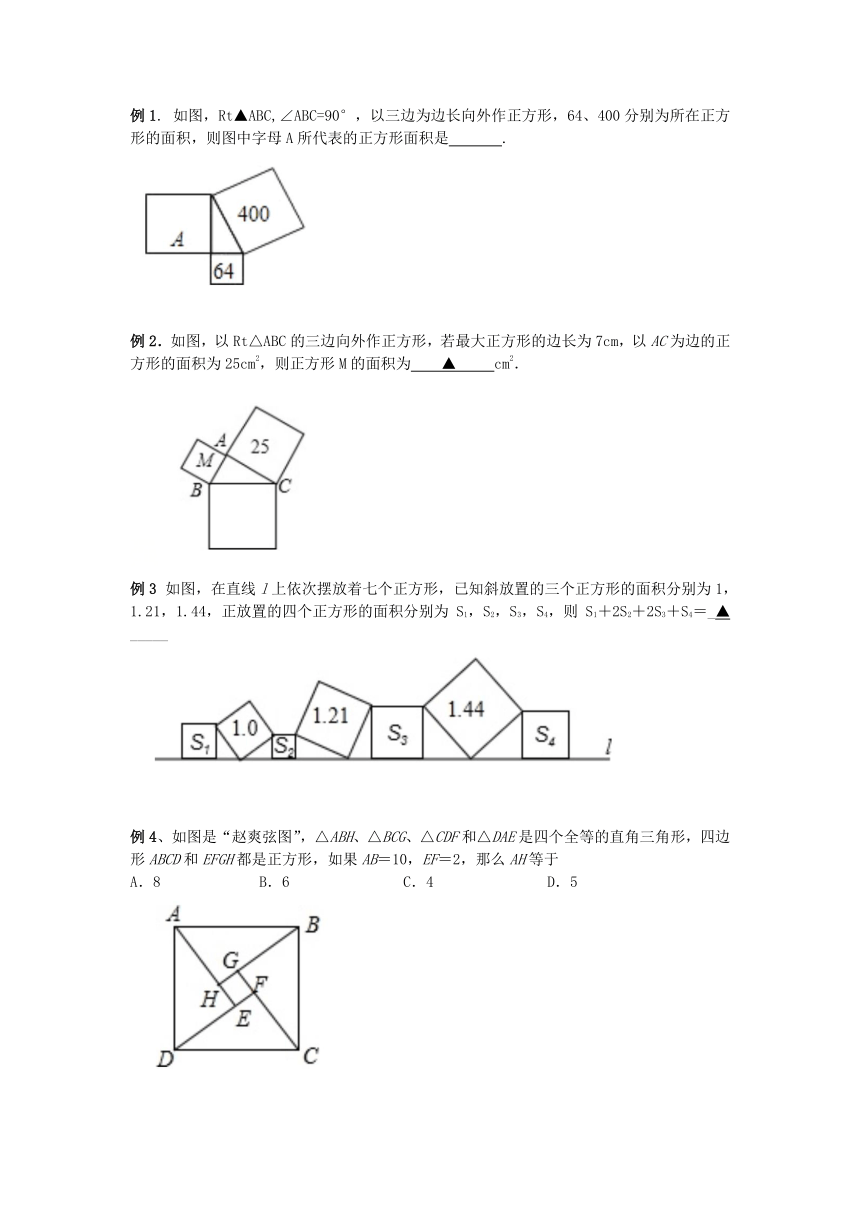
例1.
如图,Rt▲ABC,∠ABC=90°,以三边为边长向外作正方形,64、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是
.
例2.如图,以Rt△ABC的三边向外作正方形,若最大正方形的边长为7cm,以AC为边的正方形的面积为25cm2,则正方形M的面积为
▲
cm2.
例3
如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积分别为S1,S2,S3,S4,则S1+2S2+2S3+S4=_▲_____
例4、如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于
A.8
B.6
C.4
D.5
例5.
如图,在Rt▲ABC中∠B=90°,AC=25,BC=15。,以为直径的半圆的面积分别为S1、S2,则S1-S2=
.
例6
.
如图,以RT▲ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=6,则图中阴影部分的面积之和为
.
例7.
2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的而积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是
A
.2
B.
0.5
C.
13
D.1
例8.如图,由四个全等的直角三角形与中间的小正方形拼成的大正方形图案是某届国际数学大会的会标,如果大正方形的面积为16,小正方形的面积为3,直角三角形的两直角边分别为a和b,那么(a+b)2的值为(
)
A.?256
B.?169
C.?29
D.?48
例9“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为…………………………………………………………………………( )
A.3
B.4
C.5
D.6
例10.如图,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,若图中四边形ABCD和四边形EFGH都是正方形,▲ABF、▲BCG、▲CDH、▲DAE是四个全等的直角三角形,若EF=2,DE=8,则AB的长为
.
例11.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,小正方形的面积是1,
直角三角形的两条直角边的长分别是a和b,那么(a+b)2的值为
A.
49
B.
25
C.
13
D.
1
例12.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是(
)
A.13
B.26
C.47
D.94
例13.
如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=15,则S2的值是(
)
A.
3
B.
C.
5
D.
例14.
如图,则小正方形的面积S=
例15
.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载,如图(a)是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理图,(b)是由图(a)放入长方形内得到的.
∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在
长方形KLMJ的边上,则长方形KIMJ的面积为
A.90
B.100
C.110
D.121
例16实践与探索
(1)小明在玩积木游戏时,把三个正方形积木摆成一定的形状,俯视图如图①,
问题(1):若此中的三角形△DEF为直角三角形,P的面积为9,Q的面积为15,则M的面积为
▲
。
问题(2):若P的面积为36cm2,Q的面积为64cm2同时M的面积为100cm2,则△DEF为
▲
三角形。
(2)图形变化:I.如图②,分别以直角三角形的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积之间有什么关系吗?请说明理由。
(3)如图③,如果直角三角形两直角边的长分别为3和4,以直角三角形的三边为直径作半圆,你能利用上面I中的结论求出阴影部分的面积吗?阴影部分面积为
▲
。(直接写出答案)
例17在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需要求△ABC的高,而借用网格就能计算出它的面积,这种方法叫做构图法.
(1)△ABC的面积为 _________
(2)若△DEF三边的长分别为,2,,请在图①的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
(3)利用第(2)小题解题方法完成下题:如图②,一个六边形绿化区ABCDEF被分割成7个部分,其中正方形ABQP,CDRQ,EFPR的面积分别为13,20,29,且△PQR、△BCQ、△DER、△APF的面积相等,求六边形绿化区ABCDEF的面积.
1、勾股定理:
直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2。
2、勾股定理的逆定理:
如果三角形的三边长a,b,c有关系a2+b2=c2,那么这个三角形是直角三角形。
3、勾股数:
满足a2+b2=c2的三个正整数,称为勾股数。
若是勾股数组,则na、nb、nc也是勾股数组。
4、简单运用:
⑴勾股定理——常用于求边长、周长、面积;
理解:①已知直角三角形的两边求第三边,并能求出周长、面积。
②用于证明线段平方关系的问题。
③利用勾股定理,作出长为的线段
⑵勾股定理的逆定理——常用于判断三角形的形状;
理解:①确定最大边(不妨设为c);?
②若c2=a2+b2,则△ABC是以∠C为直角的三角形;?
若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);
?
若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)
考点1:直角三角形的判断
例1下列四组线段中,可以构成直角三角形的是(
▲
)
A.5,6,7
B.0.7,2.4,2.5
C.1,1,2
D.1,,3
例2.
下列各数组中,不是勾股数组的是(
▲
)
A.5,12,13
B.9,40,
41
C.8,12,15
D.3,4,5
例3
下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是(
)
A.5cm,12cm,13cm
B.1cm,1
cm,cm
C.1cm,2
cm,
cm
D.cm,2cm,
cm
例4判断由线段a、b、c组成的三角形是不是直角三角形.
(1)a=,b=1,c=;
(2)a=40
,b=50,c=60;
(3)a=35,b=12,c=37
例5
满足下列条件的三角形中,不是直角三角形的是(
)
A.三内角之比为1∶2∶3
B.三边长的平方之比为1∶2∶3
C.三边长之比为3∶4∶5
D.三内角之比为3∶4∶5
例6.下列给出的三条线段的长,能组成直角三角形的是
A.
1、2、3
B.
2、3、4
C.、、
D.
5、12、13
例7下列三角形中,可以构成直角三角形的有
A.三边长分别为2,2,3
B.三边长分别为3,3,5
C.三边长分别为4,5,6
D.三边长分别为1.5,2,2.5
例8
下列各组数中,不能构成直角三角形的一组是(
)
A.1,2,
B.1,2,
C.3,4,5
D.
6,8,12
考点2:勾股定理的证明
例1如图,将Rt△ABC绕其锐角顶点A旋转90°得到Rt△ADE,连接BE,延长DE,BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.
(1)判断△ABE的形状,并证明你的结论;
(2)用含b的代数式表示四边形ABFE的面积;
(3)求证:a2+b2=c2.
例2利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称
为弦图.观察图形,验证:c2=a2+b2.
例3一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新
的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′
的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′
的面积验证勾股定理:a2+b2=c2.
考点3:关于勾股定理几个重要的图形(勾股树、赵爽弦图)
例1.
如图,Rt▲ABC,∠ABC=90°,以三边为边长向外作正方形,64、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是
.
例2.如图,以Rt△ABC的三边向外作正方形,若最大正方形的边长为7cm,以AC为边的正方形的面积为25cm2,则正方形M的面积为
▲
cm2.
例3
如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积分别为S1,S2,S3,S4,则S1+2S2+2S3+S4=_▲_____
例4、如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于
A.8
B.6
C.4
D.5
例5.
如图,在Rt▲ABC中∠B=90°,AC=25,BC=15。,以为直径的半圆的面积分别为S1、S2,则S1-S2=
.
例6
.
如图,以RT▲ABC的三边为斜边分别向外作等腰直角三角形,若斜边AB=6,则图中阴影部分的面积之和为
.
例7.
2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的而积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是
A
.2
B.
0.5
C.
13
D.1
例8.如图,由四个全等的直角三角形与中间的小正方形拼成的大正方形图案是某届国际数学大会的会标,如果大正方形的面积为16,小正方形的面积为3,直角三角形的两直角边分别为a和b,那么(a+b)2的值为(
)
A.?256
B.?169
C.?29
D.?48
例9“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为…………………………………………………………………………( )
A.3
B.4
C.5
D.6
例10.如图,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,若图中四边形ABCD和四边形EFGH都是正方形,▲ABF、▲BCG、▲CDH、▲DAE是四个全等的直角三角形,若EF=2,DE=8,则AB的长为
.
例11.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,小正方形的面积是1,
直角三角形的两条直角边的长分别是a和b,那么(a+b)2的值为
A.
49
B.
25
C.
13
D.
1
例12.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是(
)
A.13
B.26
C.47
D.94
例13.
如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=15,则S2的值是(
)
A.
3
B.
C.
5
D.
例14.
如图,则小正方形的面积S=
例15
.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载,如图(a)是由边长相等的小正方形和直角三角形构成的,可以用其面积验证勾股定理图,(b)是由图(a)放入长方形内得到的.
∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在
长方形KLMJ的边上,则长方形KIMJ的面积为
A.90
B.100
C.110
D.121
例16实践与探索
(1)小明在玩积木游戏时,把三个正方形积木摆成一定的形状,俯视图如图①,
问题(1):若此中的三角形△DEF为直角三角形,P的面积为9,Q的面积为15,则M的面积为
▲
。
问题(2):若P的面积为36cm2,Q的面积为64cm2同时M的面积为100cm2,则△DEF为
▲
三角形。
(2)图形变化:I.如图②,分别以直角三角形的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积之间有什么关系吗?请说明理由。
(3)如图③,如果直角三角形两直角边的长分别为3和4,以直角三角形的三边为直径作半圆,你能利用上面I中的结论求出阴影部分的面积吗?阴影部分面积为
▲
。(直接写出答案)
例17在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需要求△ABC的高,而借用网格就能计算出它的面积,这种方法叫做构图法.
(1)△ABC的面积为 _________
(2)若△DEF三边的长分别为,2,,请在图①的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
(3)利用第(2)小题解题方法完成下题:如图②,一个六边形绿化区ABCDEF被分割成7个部分,其中正方形ABQP,CDRQ,EFPR的面积分别为13,20,29,且△PQR、△BCQ、△DER、△APF的面积相等,求六边形绿化区ABCDEF的面积.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
