苏科版八年级数学上册第五章平面直角坐标系培优专题训练(word版无答案)
文档属性
| 名称 | 苏科版八年级数学上册第五章平面直角坐标系培优专题训练(word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 139.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 10:13:56 | ||
图片预览

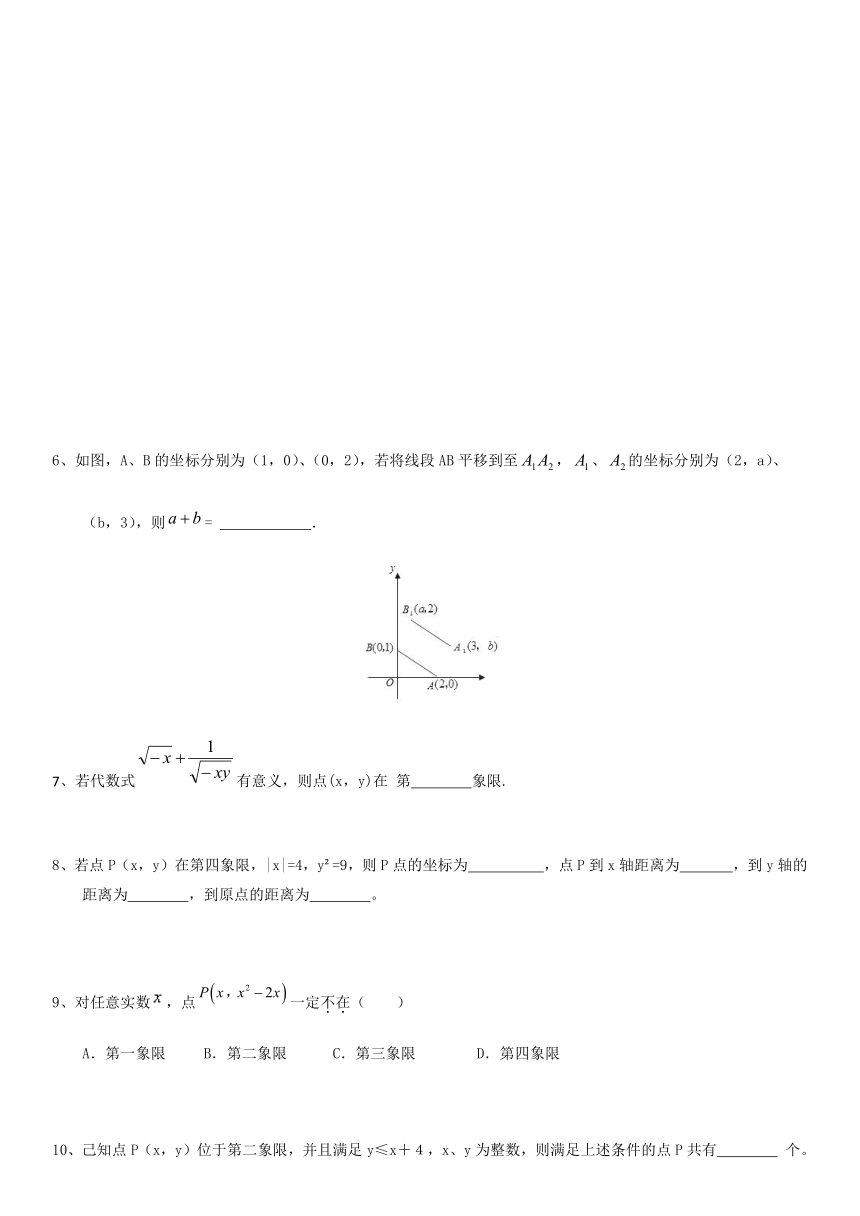


文档简介
平面直角坐标系培优专题训练
1、根据指令[S,A](S≥0,0°(1)若给机器人下了一个指令[6,30],则机器人应移动到点_________;
(2)请你给机器人下一个指令_________,使其移到点(-12,12)?
2、有甲、乙、丙三人所处位置不同。甲说:“以我为坐标原点,乙的位置是(2,3)”。丙说:“以我为坐标原点,乙的位置是(-3,-2)”,则以乙为坐标原点,甲、丙的坐标是(已知三人建立坐标时,轴轴正方向相同)(
)A.(-3,-2)(2,-3)
B.(-3,
2)(2,3)
C.(-2,-3)(3,2)
D.(-3,-2)(-2,-3)
3、在平面直角坐标系中,点A的坐标为(3,4),将线段OA绕点O顺时针旋转90°得到线段,则点的坐标是
.
4、如图,已知边长为1的正方形OABC在直角坐标系中,A、B两点在第一象限,OA与x轴的夹角为30°。
则A、B、C的坐标分别为
。
5、如图,已知ΔABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6,
∠BCD=45°。
①求A、B的坐标;②求AB中点M的坐标。
如图,A、B的坐标分别为(1,0)、(0,2),若将线段AB平移到至,、的坐标分别为(2,a)、
(b,3),则=
.
7、若代数式有意义,则点(x,y)在
第
象限.
8、若点P(x,y)在第四象限,|x|=4,y?=9,则P点的坐标为
,点P到x轴距离为
,到y轴的距离为
,到原点的距离为
。
9、对任意实数,点一定不在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10、己知点P(x,y)位于第二象限,并且满足y≤x+4,x、y为整数,则满足上述条件的点P共有
个。
11、已知点P(2a-8,2-a)是第三象限的整点(横、纵坐标均为整数),则P点的坐标是___
___.
12、如果│3x-13y+a│+│x+3y-2│=0,那么点P(x,y)关于x轴的对称点在第一象限,则a的取值范围为
13、已知点A(2,-3),线段AB与坐标轴没有交点,则点B的坐标可能是
(
)
A.(-1,-2)
B.(
3,-2)
C.(1,2)
D.(-2,3)
14、若A(3,-5),AB∥x轴,且AB=2,则B点的坐标为
。
15、.已知线段
MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为
.
16、已知线段CD是由线段AB平移得到的,点A(﹣1,4)的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的坐标为
17、如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为_______.
12、如图,平面直角坐标系中有一个正六边形ABCDEF,其中点C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,过点(45,2)的是点_______.
如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将
△OA2B2变换成△OA3B3,已知A(1,3)、A1(2,3)、A2(4,3)、A3(8,3),B(2,0)、B1(4,0)、B2(8,0)、B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标是__________,B4的坐标是__________.
(2)若按第一题找出的规律,将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有
何变化,找出规律,推测An的坐标是________,Bn的坐标是__________.
14、在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是
15、如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为
.
如图,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等边三角形(点A、C、P按逆时针方向排列);当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).
初步探究(1)写出点B的坐标______;
点C在x轴上移动过程中,当等边三角形ACP的顶点P在第三象限时,连接BP,求证:△AOC≌△ABP.
深入探究
当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论;并求出这个图形所对应的函数表达式.
拓展应用
(4)点C在x轴上移动过程中,当△POB为等腰三角形时,直接写出此时点C的坐标.
18、类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(﹣2)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图1中画出四边形OABC.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
19、数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
(1)探究的几何意义:如图①,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),即OP=|x|,OQ=|y|,在△OPM中,PM=OQ=|y|,则MO===,因此,的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离OM.
①的几何意义可以理解为点N1
(填写坐标)与点O(0,0)之间的距离N1O;
②点N2(5,﹣1)与点O(0,0)之间的距离ON2为
.
探究的几何意义:如图②,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),
由探究(1)可知,A′O=,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB=,因此的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离.
探究的几何意义:请仿照探究二(2)的方法,在图③中画出图形,
那么的几何意义可以理解为点C
(填写坐标)与点D(x,y)之间的距离.
(4)拓展应用:
①+的几何意义可以理解为:点A(x,y)与点E(1,﹣4)的距离与点A(x,y)与点F
(填写坐标)的距离之和.
②+的最小值为
(直接写出结果)
1、根据指令[S,A](S≥0,0°
(2)请你给机器人下一个指令_________,使其移到点(-12,12)?
2、有甲、乙、丙三人所处位置不同。甲说:“以我为坐标原点,乙的位置是(2,3)”。丙说:“以我为坐标原点,乙的位置是(-3,-2)”,则以乙为坐标原点,甲、丙的坐标是(已知三人建立坐标时,轴轴正方向相同)(
)A.(-3,-2)(2,-3)
B.(-3,
2)(2,3)
C.(-2,-3)(3,2)
D.(-3,-2)(-2,-3)
3、在平面直角坐标系中,点A的坐标为(3,4),将线段OA绕点O顺时针旋转90°得到线段,则点的坐标是
.
4、如图,已知边长为1的正方形OABC在直角坐标系中,A、B两点在第一象限,OA与x轴的夹角为30°。
则A、B、C的坐标分别为
。
5、如图,已知ΔABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6,
∠BCD=45°。
①求A、B的坐标;②求AB中点M的坐标。
如图,A、B的坐标分别为(1,0)、(0,2),若将线段AB平移到至,、的坐标分别为(2,a)、
(b,3),则=
.
7、若代数式有意义,则点(x,y)在
第
象限.
8、若点P(x,y)在第四象限,|x|=4,y?=9,则P点的坐标为
,点P到x轴距离为
,到y轴的距离为
,到原点的距离为
。
9、对任意实数,点一定不在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10、己知点P(x,y)位于第二象限,并且满足y≤x+4,x、y为整数,则满足上述条件的点P共有
个。
11、已知点P(2a-8,2-a)是第三象限的整点(横、纵坐标均为整数),则P点的坐标是___
___.
12、如果│3x-13y+a│+│x+3y-2│=0,那么点P(x,y)关于x轴的对称点在第一象限,则a的取值范围为
13、已知点A(2,-3),线段AB与坐标轴没有交点,则点B的坐标可能是
(
)
A.(-1,-2)
B.(
3,-2)
C.(1,2)
D.(-2,3)
14、若A(3,-5),AB∥x轴,且AB=2,则B点的坐标为
。
15、.已知线段
MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为
.
16、已知线段CD是由线段AB平移得到的,点A(﹣1,4)的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的坐标为
17、如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为_______.
12、如图,平面直角坐标系中有一个正六边形ABCDEF,其中点C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,过点(45,2)的是点_______.
如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将
△OA2B2变换成△OA3B3,已知A(1,3)、A1(2,3)、A2(4,3)、A3(8,3),B(2,0)、B1(4,0)、B2(8,0)、B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标是__________,B4的坐标是__________.
(2)若按第一题找出的规律,将△OAB进行n次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有
何变化,找出规律,推测An的坐标是________,Bn的坐标是__________.
14、在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是
15、如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为
.
如图,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等边三角形(点A、C、P按逆时针方向排列);当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).
初步探究(1)写出点B的坐标______;
点C在x轴上移动过程中,当等边三角形ACP的顶点P在第三象限时,连接BP,求证:△AOC≌△ABP.
深入探究
当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论;并求出这个图形所对应的函数表达式.
拓展应用
(4)点C在x轴上移动过程中,当△POB为等腰三角形时,直接写出此时点C的坐标.
18、类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(﹣2)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图1中画出四边形OABC.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
19、数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
(1)探究的几何意义:如图①,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),即OP=|x|,OQ=|y|,在△OPM中,PM=OQ=|y|,则MO===,因此,的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离OM.
①的几何意义可以理解为点N1
(填写坐标)与点O(0,0)之间的距离N1O;
②点N2(5,﹣1)与点O(0,0)之间的距离ON2为
.
探究的几何意义:如图②,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),
由探究(1)可知,A′O=,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB=,因此的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离.
探究的几何意义:请仿照探究二(2)的方法,在图③中画出图形,
那么的几何意义可以理解为点C
(填写坐标)与点D(x,y)之间的距离.
(4)拓展应用:
①+的几何意义可以理解为:点A(x,y)与点E(1,﹣4)的距离与点A(x,y)与点F
(填写坐标)的距离之和.
②+的最小值为
(直接写出结果)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
