湘教版(2012)初中数学七年级上册2.2 列代数式 课件(20张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学七年级上册2.2 列代数式 课件(20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 732.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 11:10:00 | ||
图片预览






文档简介
(共20张PPT)
本课内容
本节内容
2.2
列代数式
1、一个两位数,十位数字是a,个位数字是b,则这个两位数是(
)
2、我们班程煜松今天带了m元钱,借给周永康n元后,程煜松剩下的钱是曹郴旺的一半,曹郴旺今天带了多少钱?(
)
3、某工厂的产量每年增长15%,如果第一年的产量是m,那么第二年、第三年的产量分别是多少?
(
)
(
)
一、复习用字母表示数
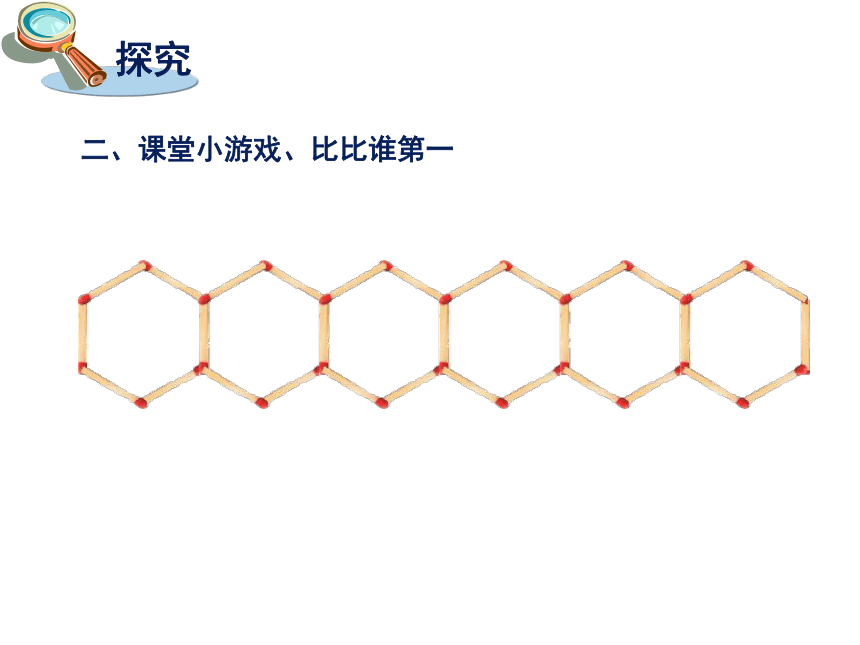
二、课堂小游戏、比比谁第一
探究
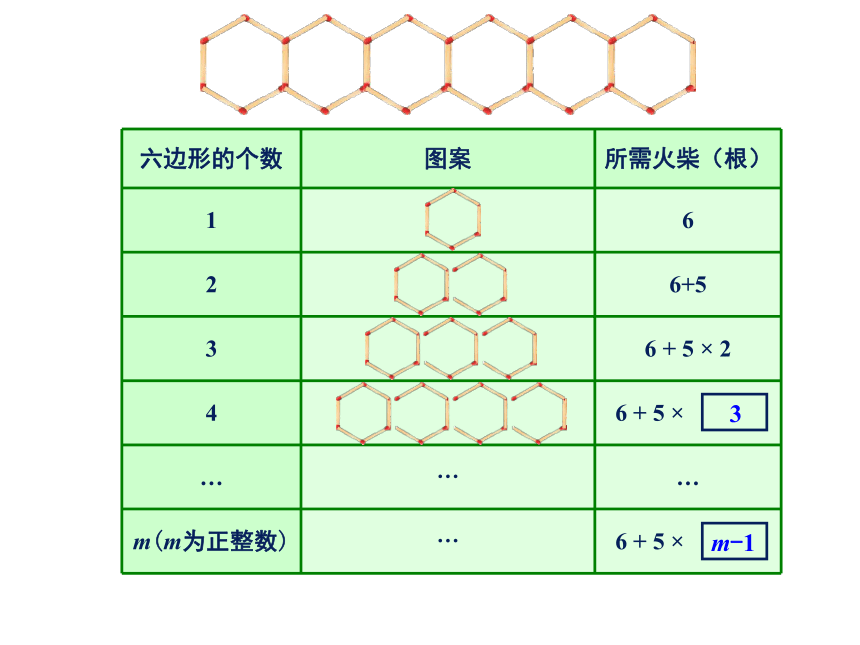
六边形的个数
图案
所需火柴(根)
1
6
2
6+5
3
6
+
5
×
2
4
6
+
5
×
…
…
…
m(m为正整数)
…
6
+
5
×
3
m-1
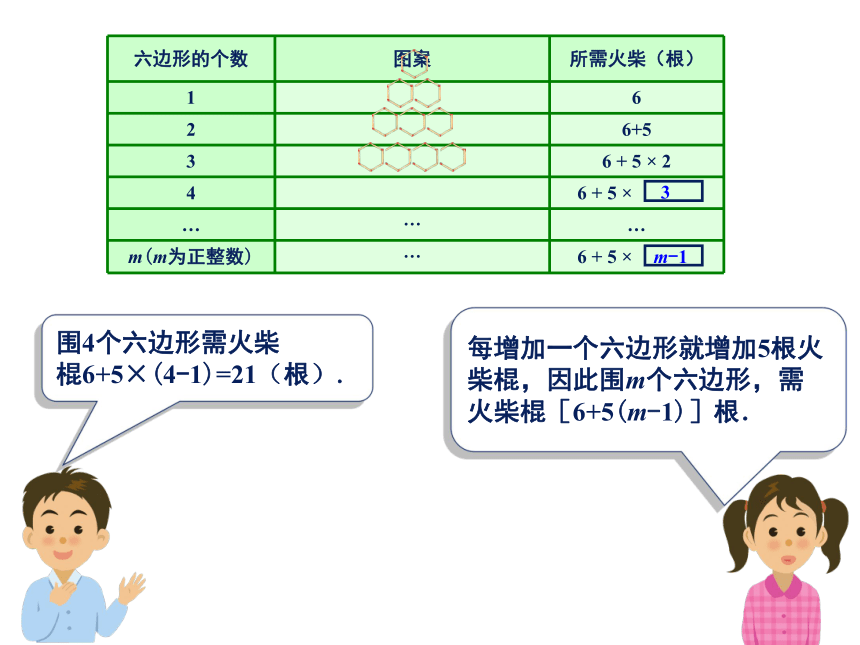
围4个六边形需火柴
棍6+5×(4-1)=21(根).
每增加一个六边形就增加5根火柴棍,因此围m个六边形,需火柴棍[6+5(m-1)]根.
六边形的个数
图案
所需火柴(根)
1
6
2
6+5
3
6
+
5
×
2
4
6
+
5
×
…
…
…
m(m为正整数)
…
6
+
5
×
3
m-1
三、小组讨论、获取新知
以上所得的式子与以前学过的数学算式有什么区别?
思考
2ab
0.6
a
+c
10a+b
2(m-n)
(1+25%)m
单独一个字母或者一个数也是代数式.
前面我们列出了一些式子,如10a+b,2(m-n),(1+25%)m,
0.6
a
+c,2ab,6
+5(m-1),
像这样,把数与表示数的字母用运算符号连接而成的式子叫做代数式.
例如-5,0,
23,
-m,n都是代数式.
概念
四、归纳总结、获取新知
1、下列各式中,判断下列式子是否是代数式?
①
2x-y;
②
a2+3ab-2b2;
③
a;
④
3;
⑤
7x>5;
⑥
0;
⑦
2+7=9;
⑧
S=ab.
五、概念检测
一起说答案
例1
用代数式表示:
(1)a的7倍与2b的差;
(2)x,
y
两数的平方和减去两数积的2倍;
(3)a的倒数与b的和.
举
例
解
:
(1)
7a
-2b;
(2)
x2+
y2-2xy
;
(3)
.
六、例题分析、巩固新知
例2
(1)已知铅笔每支x元,练习本每本y元.小明买铅笔5支,练习本6本,需多少元?
举
例
解:(1)需(5x+
6y)元;
(2)小兰骑自行车的速度是(v+10)km/h,
从家到学校需
(2)小兰的家距学校5
km,她步行的速度是v
km/h.
而骑自行车比步行快10
km/h.
她骑自行车的速度是多少?她骑自行车从家到学校需多长时间?
六、例题分析、巩固新知
举出实例,说说代数式25a可以表示什么.
如果苹果的价格是每千克a元,买25kg苹果则需要25a元.
说一说
如果用am/s表示小强跑步的速度,则他跑25s所跑的路程为25am.
七、结合实际、应用新知
练习
1.
用代数式填空:
(1)某阶梯教室第一排有8个座位,第二排有10个座
位,以后每排都比它前一排多2个座位,那么第n
排有
个座位;
[8+2(n-1)]
(2)一批货物共x
t,第一天售出
,第二天售出剩下的
一半,还剩下货物
t
.
[x
-
x
-
(
x
-
x)]
八、课堂练习、应用新知
(1)a
与b的和的平方;
2.
列代数式:
(2)一件进价为x元的商品,卖出后利润率为
25%,那么这件商品的利润是多少元?
(利润=进价×利润率)
解:(a+b)2
解:0.25x
元
练习
八、课堂练习、应用新知
(3)某储户存入一年期定期储蓄10000元,一年期定期储
蓄的年利率为a%,则一年到期后,该储户可得本息
和(本金与利息的和)多少元?(利息=本金×年利
率×年数)
解:(10000+100a)元
练习
七、课堂练习、应用新知
解
中考
试题
例1
D
“x的
与y的和”用代数式表示为(
).
A.
(x
+
y)
B.x
+
+
y
C.
x
+
y
D.
x
+
y
分析
列代数式时,根据语序确定运算顺序.
依题意,得
x
+y.故,应选择D
解
中考
试题
例2
某书店出售图书的同时,推出一项租书业务,每租看1本书,租期不超过3天;每天租金a元;租期超过3天,从第4天开始每天加收b元,如果租看7天归还,那么租金为
元.
依题意,得(7a+4b)元.
(7a+4b)
解
中考
试题
例3
如图所示,有一块长为a,宽为b的长方形铝片,四角各载去一个相同的边长为x的正方形,折起来做成一个没有盖的盒子,则此盒子的容积的表达式应该是(
).
A.
V
=
x2(a-x)(b-x)
B.
V
=
x
(a-x)(b-x)
C.
V
=
x(a-2x)(b-2x)
D.
V
=
x(a-2x)(b-2x)
由题意可知,盒子的底面长为(a-2x),宽为(b-2x),高为x.因此,盒子的容积为:V=x(a-2x)(b-2x).
故,应选择D.
分析
本题应采用直接法求解.
D
八、课堂小结、说一说
通过这节课的学习,你有什么收获?
九、作业布置
教材61页和62页A组第1题和第2题
感谢您的聆听!
本课内容
本节内容
2.2
列代数式
1、一个两位数,十位数字是a,个位数字是b,则这个两位数是(
)
2、我们班程煜松今天带了m元钱,借给周永康n元后,程煜松剩下的钱是曹郴旺的一半,曹郴旺今天带了多少钱?(
)
3、某工厂的产量每年增长15%,如果第一年的产量是m,那么第二年、第三年的产量分别是多少?
(
)
(
)
一、复习用字母表示数
二、课堂小游戏、比比谁第一
探究
六边形的个数
图案
所需火柴(根)
1
6
2
6+5
3
6
+
5
×
2
4
6
+
5
×
…
…
…
m(m为正整数)
…
6
+
5
×
3
m-1
围4个六边形需火柴
棍6+5×(4-1)=21(根).
每增加一个六边形就增加5根火柴棍,因此围m个六边形,需火柴棍[6+5(m-1)]根.
六边形的个数
图案
所需火柴(根)
1
6
2
6+5
3
6
+
5
×
2
4
6
+
5
×
…
…
…
m(m为正整数)
…
6
+
5
×
3
m-1
三、小组讨论、获取新知
以上所得的式子与以前学过的数学算式有什么区别?
思考
2ab
0.6
a
+c
10a+b
2(m-n)
(1+25%)m
单独一个字母或者一个数也是代数式.
前面我们列出了一些式子,如10a+b,2(m-n),(1+25%)m,
0.6
a
+c,2ab,6
+5(m-1),
像这样,把数与表示数的字母用运算符号连接而成的式子叫做代数式.
例如-5,0,
23,
-m,n都是代数式.
概念
四、归纳总结、获取新知
1、下列各式中,判断下列式子是否是代数式?
①
2x-y;
②
a2+3ab-2b2;
③
a;
④
3;
⑤
7x>5;
⑥
0;
⑦
2+7=9;
⑧
S=ab.
五、概念检测
一起说答案
例1
用代数式表示:
(1)a的7倍与2b的差;
(2)x,
y
两数的平方和减去两数积的2倍;
(3)a的倒数与b的和.
举
例
解
:
(1)
7a
-2b;
(2)
x2+
y2-2xy
;
(3)
.
六、例题分析、巩固新知
例2
(1)已知铅笔每支x元,练习本每本y元.小明买铅笔5支,练习本6本,需多少元?
举
例
解:(1)需(5x+
6y)元;
(2)小兰骑自行车的速度是(v+10)km/h,
从家到学校需
(2)小兰的家距学校5
km,她步行的速度是v
km/h.
而骑自行车比步行快10
km/h.
她骑自行车的速度是多少?她骑自行车从家到学校需多长时间?
六、例题分析、巩固新知
举出实例,说说代数式25a可以表示什么.
如果苹果的价格是每千克a元,买25kg苹果则需要25a元.
说一说
如果用am/s表示小强跑步的速度,则他跑25s所跑的路程为25am.
七、结合实际、应用新知
练习
1.
用代数式填空:
(1)某阶梯教室第一排有8个座位,第二排有10个座
位,以后每排都比它前一排多2个座位,那么第n
排有
个座位;
[8+2(n-1)]
(2)一批货物共x
t,第一天售出
,第二天售出剩下的
一半,还剩下货物
t
.
[x
-
x
-
(
x
-
x)]
八、课堂练习、应用新知
(1)a
与b的和的平方;
2.
列代数式:
(2)一件进价为x元的商品,卖出后利润率为
25%,那么这件商品的利润是多少元?
(利润=进价×利润率)
解:(a+b)2
解:0.25x
元
练习
八、课堂练习、应用新知
(3)某储户存入一年期定期储蓄10000元,一年期定期储
蓄的年利率为a%,则一年到期后,该储户可得本息
和(本金与利息的和)多少元?(利息=本金×年利
率×年数)
解:(10000+100a)元
练习
七、课堂练习、应用新知
解
中考
试题
例1
D
“x的
与y的和”用代数式表示为(
).
A.
(x
+
y)
B.x
+
+
y
C.
x
+
y
D.
x
+
y
分析
列代数式时,根据语序确定运算顺序.
依题意,得
x
+y.故,应选择D
解
中考
试题
例2
某书店出售图书的同时,推出一项租书业务,每租看1本书,租期不超过3天;每天租金a元;租期超过3天,从第4天开始每天加收b元,如果租看7天归还,那么租金为
元.
依题意,得(7a+4b)元.
(7a+4b)
解
中考
试题
例3
如图所示,有一块长为a,宽为b的长方形铝片,四角各载去一个相同的边长为x的正方形,折起来做成一个没有盖的盒子,则此盒子的容积的表达式应该是(
).
A.
V
=
x2(a-x)(b-x)
B.
V
=
x
(a-x)(b-x)
C.
V
=
x(a-2x)(b-2x)
D.
V
=
x(a-2x)(b-2x)
由题意可知,盒子的底面长为(a-2x),宽为(b-2x),高为x.因此,盒子的容积为:V=x(a-2x)(b-2x).
故,应选择D.
分析
本题应采用直接法求解.
D
八、课堂小结、说一说
通过这节课的学习,你有什么收获?
九、作业布置
教材61页和62页A组第1题和第2题
感谢您的聆听!
同课章节目录
