第六章二元一次方程组6.1-6.2复习课件-冀教版七年级数学下册(共28张PPT)
文档属性
| 名称 | 第六章二元一次方程组6.1-6.2复习课件-冀教版七年级数学下册(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
第六章二元一次方程组
6.1-6.2复习课件
考点一:
二元一次方程与二元一次方程组
含有两个未知数,并且含未知数的项的次数都是1的整式方程叫二元一次方程.
注意:二元一次方程必须满足下面四个条件含有:
①
必须含有两个未知数②
未知项的次数必须是1
③
未知项的系数不能是
0④
方程两边的代数式必须是整式
含有两个未知数,并且含未知数的项的次数
都是1的方程组,叫做二元一次方程组。
1、下列是二元一次方程组的是
(
)
+
y
=3
x
1
2x+y
=0
(A)
3x
-1
=0
2y
=5
(B)
x
+
y
=
7
3y
+2xy
=
4
(c)
5x
-
y
=
-2
3y
+
x
=
4
(D)
2
B
解:由题意,得|a|-2=1,且a+3≠0,故a=3
b2-8=1且b-3≠0,故b=-3
3.知(a+3)x|a|-2+(b-3)yb2-8-1是一个关于x,y的二元一次方程,求a的值
2.若方程xm-2+5y3n-5是二元一次方程,则
m,n的值分别为_______.
m=3
n=2
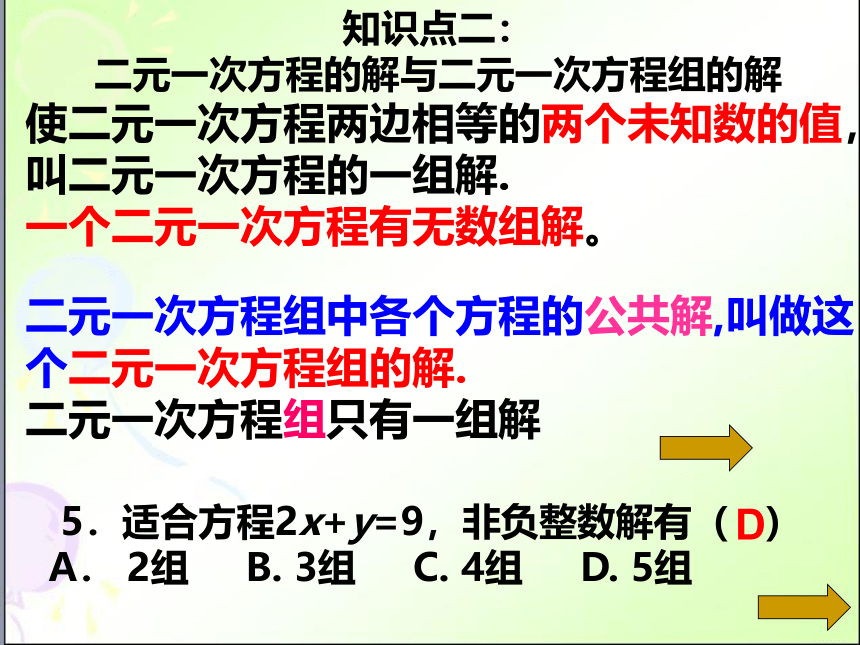
5.适合方程2x+y=9,非负整数解有(
)
A.
2组
B.
3组
C.
4组
D.
5组
D
知识点二:
二元一次方程的解与二元一次方程组的解
使二元一次方程两边相等的两个未知数的值,叫二元一次方程的一组解.
一个二元一次方程有无数组解。
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
二元一次方程组只有一组解
4.在上学的路上,小明对小丽和小红说:”谁能借我5元钱?”小丽说:”我带了10元整。”小红说:“我可以借给你,我有10元零钱。”请问小红手中的钱是怎样的?有几种情况。
解:设小红手中的钱一元x张,五元y张,则
x+5y=10
x=10-5y
y=0
x=10
y=1
x=5
y=2
x=0
答:小红手中的钱有3中情况,可能10张一元,或
5张一元、1张五元,或2张5元。
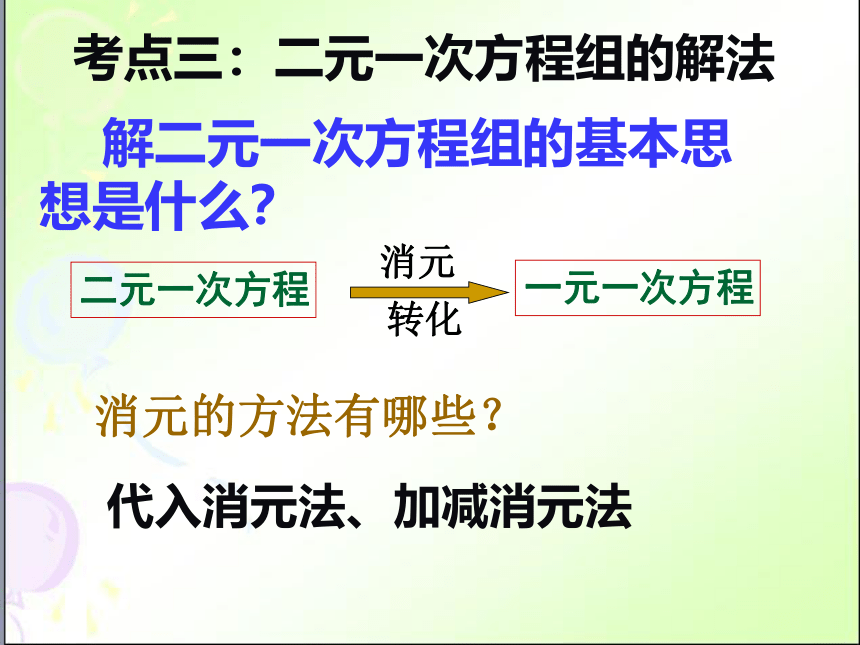
考点三:二元一次方程组的解法
解二元一次方程组的基本思想是什么?
二元一次方程
一元一次方程
消元
转化
消元的方法有哪些?
代入消元法、加减消元法
6.
代入消元法
(1)有一个方程是:“用一个未知数的代数式表示另一个未知数”的形式.
(2)方程组中某一未知数的系数是
1
或
-1.
y=x-6
x+2y=9
①
②
2x
+3y=
17
4x-y=
13
①
②
练
习
解方程组
x
+2y=
9
y
=
x-
6
①
②
解:
把②代入①得:
x+2(x
–
6)=
9
解得x=
7
把x
=
7代入②,得
y=
1
∴方程组的解是
x
=
7
y
=
1
用代入法解方程组
2x+3y=17
①
4
x-y=13
②
解:
∴原方程组的解是
x=4
y=3
由②
,得
y=4x
-
13
③
把③代入①
,得
2x+3(4x-13)=16
2x+12x-39
=17
14x=
56
x=4
把x=4代入③
,得
y=3
(1)方程组中同一未知数的系数相等或相反数.
(2)方程组中同一未知数的系数是变成相同或相反数.
5x
+3y=
16
2x
-3y=
-2
①
②
2x
-5y=
7
2x
+3y=
-1
①
②
3x
+2y=
5
6x
-5y=
1
①
②
7.
加减消元法
解:①+②得:
7x=14
将x=2代入①,得:5×2+3y=16
∴y=2
∴x=2
所以原方程组的解是
①
②
∴x=2
x=2
y=2
2x-5y=7
①
2x+3y=-1
②
解:
②-①得:
8y=-8
∴y=-1
将y
=-1代入①,得:
2x-5×(-1)=7
∴x=1
∴原方程组的解是
x=1
y=-1
①×2得
6x+4y=10
③
所以原方程组的解是
①
②
③-
②得:
9
y=9
∴y=1
将y
=1代入①,3x+2×1=5
∴x=1
8.用加减法解方程组
3x-5y=6①
2x-5y=7②
具体解
法如下
(1)
①-
②得x=1
(2)把x=1代入①得y=-1.
(3)∴
x=1
y=-1
其中出现错误的一步是(
)
A(1)
B(2)
C(3)
A
9.指出下列方程组求解过程中的错误步骤,并正确求解。
7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解:①-②,得
-2x=12
x
=-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x
=2
10.用加减消元法解方程组:
解:由①×6,得
解:①×6得:2x+3y=4
③
由②×4,得
2x
-
y=8
④
由③-④得:
y=
-1
所以原方程组
的解是
把y=
-1代入④
,
解得:
②
①
②×4得:2x-y=8④
④
11.认真观察方程组
3x-2y=7①
2x-3y=8②
x+y=(
)
x-y=(
)
-1
3
解:①+②得:5x-5y=15
x-y=3③
①-②得:x+y=-1④
③+④得:x=1
把x=1代入④得:
y=-2
所以原方程组的解为
y=
-2
x=
1
x=
1
y=
-2
解方程组:
阅读理解
①
②
解:
①+②得:
即
①-②得:
③
④
③+④得:
③-④得:
结论
正确吗?
根据方程组的特征,重构方程(组)
灵活应用
5
-1
1.已知二元一次方程组
,
则
,
。
2.已知
,
则
。
16
3.在
中,把①代入②得:
①②
。
整体代入
整体思想
灵活应用
5、解关于x、y的方程组
时,
小明求得正确的解是
,
而小马因看错系数
c
解得
,
试求a,b,c的值。
12.关于x、y的二元一次方程组
一次方程组
的解与二元
的解相同,求a、b的值
解:由题意得:解方程组
得
将
代入方程组
得
解得
∴a=
,
b=
ax+by=2
ax-by=4
2x+3y=10
4x-5y=-2
13.已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值
解:根据题意:得
3m+2n-16=0
3m-n-1=0
解得:
m=2
n=5
即:m+n=7
14.
已知方程2x+3y=20,x+y=8,mx+ny=-4有一组公共解,求(m+n)2017的值.
解:由题意,可列方程组
①
②
①-③得,y
=
4.
②×2得,
2x+2y=16.
③
把y
=
4代入②得,x
=
4.
4m+4n=-4,即
m+n=-1.
所以(m+n)2017=(-1)2017=-1.
把x
=
4,y
=
4代入mx+ny=-4得,
课堂检测.二元一次方程组的综合应用
2.如果
,那么
=__,
=
__
。
1.已知代数式
与
是同类项,
则m=___???
,n=___
?????
3.二元一次方程组
的解中,
x、y的值相等,则k=
.
2
1
3
2
用适当的方法解下列方程组:
(1)
掌握基本方法
(2)
已知
,则
?
①②
①-②得:
整体思想
小
结
课下作业:见微信群文件完成
第一题单选题(每个题要写过程)。
第六章二元一次方程组
6.1-6.2复习课件
考点一:
二元一次方程与二元一次方程组
含有两个未知数,并且含未知数的项的次数都是1的整式方程叫二元一次方程.
注意:二元一次方程必须满足下面四个条件含有:
①
必须含有两个未知数②
未知项的次数必须是1
③
未知项的系数不能是
0④
方程两边的代数式必须是整式
含有两个未知数,并且含未知数的项的次数
都是1的方程组,叫做二元一次方程组。
1、下列是二元一次方程组的是
(
)
+
y
=3
x
1
2x+y
=0
(A)
3x
-1
=0
2y
=5
(B)
x
+
y
=
7
3y
+2xy
=
4
(c)
5x
-
y
=
-2
3y
+
x
=
4
(D)
2
B
解:由题意,得|a|-2=1,且a+3≠0,故a=3
b2-8=1且b-3≠0,故b=-3
3.知(a+3)x|a|-2+(b-3)yb2-8-1是一个关于x,y的二元一次方程,求a的值
2.若方程xm-2+5y3n-5是二元一次方程,则
m,n的值分别为_______.
m=3
n=2
5.适合方程2x+y=9,非负整数解有(
)
A.
2组
B.
3组
C.
4组
D.
5组
D
知识点二:
二元一次方程的解与二元一次方程组的解
使二元一次方程两边相等的两个未知数的值,叫二元一次方程的一组解.
一个二元一次方程有无数组解。
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
二元一次方程组只有一组解
4.在上学的路上,小明对小丽和小红说:”谁能借我5元钱?”小丽说:”我带了10元整。”小红说:“我可以借给你,我有10元零钱。”请问小红手中的钱是怎样的?有几种情况。
解:设小红手中的钱一元x张,五元y张,则
x+5y=10
x=10-5y
y=0
x=10
y=1
x=5
y=2
x=0
答:小红手中的钱有3中情况,可能10张一元,或
5张一元、1张五元,或2张5元。
考点三:二元一次方程组的解法
解二元一次方程组的基本思想是什么?
二元一次方程
一元一次方程
消元
转化
消元的方法有哪些?
代入消元法、加减消元法
6.
代入消元法
(1)有一个方程是:“用一个未知数的代数式表示另一个未知数”的形式.
(2)方程组中某一未知数的系数是
1
或
-1.
y=x-6
x+2y=9
①
②
2x
+3y=
17
4x-y=
13
①
②
练
习
解方程组
x
+2y=
9
y
=
x-
6
①
②
解:
把②代入①得:
x+2(x
–
6)=
9
解得x=
7
把x
=
7代入②,得
y=
1
∴方程组的解是
x
=
7
y
=
1
用代入法解方程组
2x+3y=17
①
4
x-y=13
②
解:
∴原方程组的解是
x=4
y=3
由②
,得
y=4x
-
13
③
把③代入①
,得
2x+3(4x-13)=16
2x+12x-39
=17
14x=
56
x=4
把x=4代入③
,得
y=3
(1)方程组中同一未知数的系数相等或相反数.
(2)方程组中同一未知数的系数是变成相同或相反数.
5x
+3y=
16
2x
-3y=
-2
①
②
2x
-5y=
7
2x
+3y=
-1
①
②
3x
+2y=
5
6x
-5y=
1
①
②
7.
加减消元法
解:①+②得:
7x=14
将x=2代入①,得:5×2+3y=16
∴y=2
∴x=2
所以原方程组的解是
①
②
∴x=2
x=2
y=2
2x-5y=7
①
2x+3y=-1
②
解:
②-①得:
8y=-8
∴y=-1
将y
=-1代入①,得:
2x-5×(-1)=7
∴x=1
∴原方程组的解是
x=1
y=-1
①×2得
6x+4y=10
③
所以原方程组的解是
①
②
③-
②得:
9
y=9
∴y=1
将y
=1代入①,3x+2×1=5
∴x=1
8.用加减法解方程组
3x-5y=6①
2x-5y=7②
具体解
法如下
(1)
①-
②得x=1
(2)把x=1代入①得y=-1.
(3)∴
x=1
y=-1
其中出现错误的一步是(
)
A(1)
B(2)
C(3)
A
9.指出下列方程组求解过程中的错误步骤,并正确求解。
7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解:①-②,得
-2x=12
x
=-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x
=2
10.用加减消元法解方程组:
解:由①×6,得
解:①×6得:2x+3y=4
③
由②×4,得
2x
-
y=8
④
由③-④得:
y=
-1
所以原方程组
的解是
把y=
-1代入④
,
解得:
②
①
②×4得:2x-y=8④
④
11.认真观察方程组
3x-2y=7①
2x-3y=8②
x+y=(
)
x-y=(
)
-1
3
解:①+②得:5x-5y=15
x-y=3③
①-②得:x+y=-1④
③+④得:x=1
把x=1代入④得:
y=-2
所以原方程组的解为
y=
-2
x=
1
x=
1
y=
-2
解方程组:
阅读理解
①
②
解:
①+②得:
即
①-②得:
③
④
③+④得:
③-④得:
结论
正确吗?
根据方程组的特征,重构方程(组)
灵活应用
5
-1
1.已知二元一次方程组
,
则
,
。
2.已知
,
则
。
16
3.在
中,把①代入②得:
①②
。
整体代入
整体思想
灵活应用
5、解关于x、y的方程组
时,
小明求得正确的解是
,
而小马因看错系数
c
解得
,
试求a,b,c的值。
12.关于x、y的二元一次方程组
一次方程组
的解与二元
的解相同,求a、b的值
解:由题意得:解方程组
得
将
代入方程组
得
解得
∴a=
,
b=
ax+by=2
ax-by=4
2x+3y=10
4x-5y=-2
13.已知(3m+2n-16)2与|3m-n-1|互为相反数
求:m+n的值
解:根据题意:得
3m+2n-16=0
3m-n-1=0
解得:
m=2
n=5
即:m+n=7
14.
已知方程2x+3y=20,x+y=8,mx+ny=-4有一组公共解,求(m+n)2017的值.
解:由题意,可列方程组
①
②
①-③得,y
=
4.
②×2得,
2x+2y=16.
③
把y
=
4代入②得,x
=
4.
4m+4n=-4,即
m+n=-1.
所以(m+n)2017=(-1)2017=-1.
把x
=
4,y
=
4代入mx+ny=-4得,
课堂检测.二元一次方程组的综合应用
2.如果
,那么
=__,
=
__
。
1.已知代数式
与
是同类项,
则m=___???
,n=___
?????
3.二元一次方程组
的解中,
x、y的值相等,则k=
.
2
1
3
2
用适当的方法解下列方程组:
(1)
掌握基本方法
(2)
已知
,则
?
①②
①-②得:
整体思想
小
结
课下作业:见微信群文件完成
第一题单选题(每个题要写过程)。
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
