2020-2021学年上海市松江区九年级上学期期中数学试卷 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市松江区九年级上学期期中数学试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 06:40:52 | ||
图片预览


文档简介
2020-2021学年上海市松江区九年级第一学期期中数学试卷
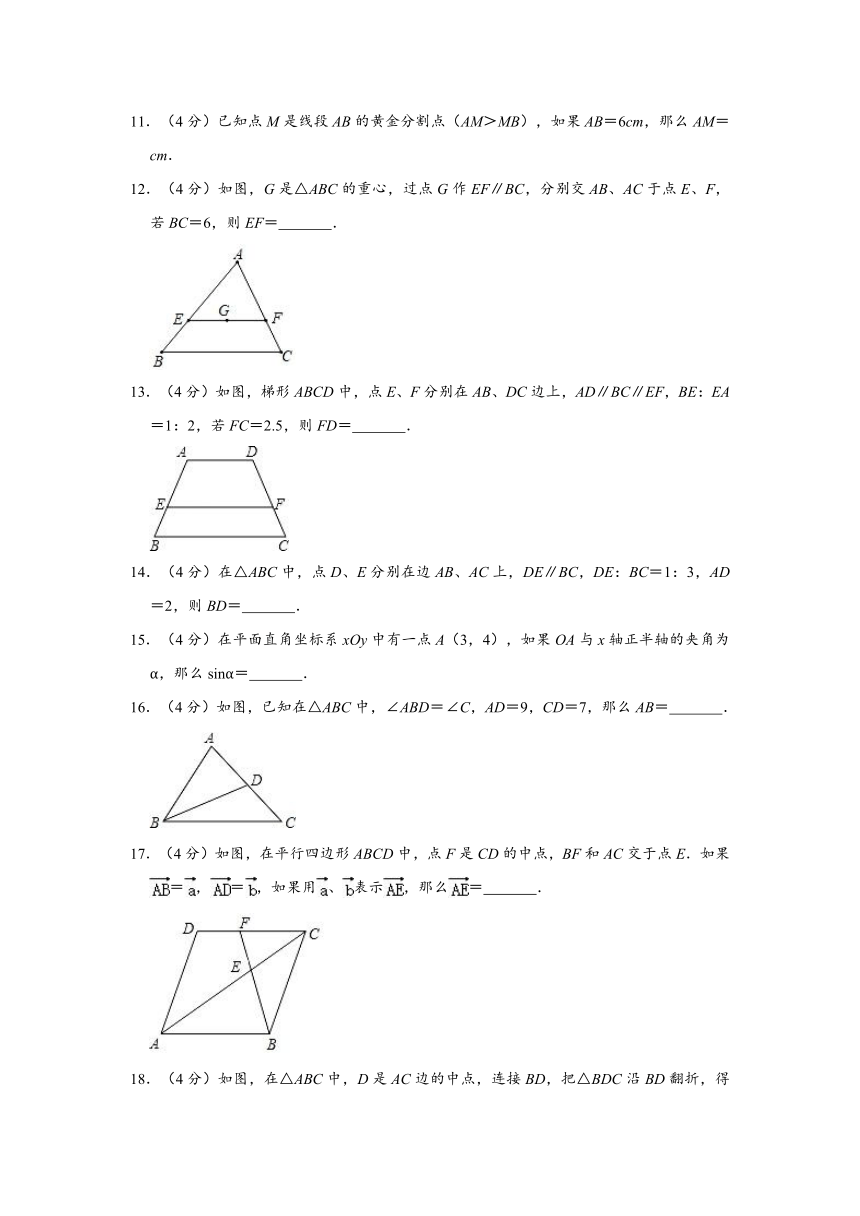
一、选择题(共6小题).
1.(4分)下列各组线段中,能组成比例线段的( )
A.2,3,4,5 B.2,3,4,6 C.2,3,5,7 D.3,4,5,6
2.(4分)下列图形中一定相似的是( )
A.两个等腰三角形 B.两个菱形
C.两个直角三角形 D.两个正方形
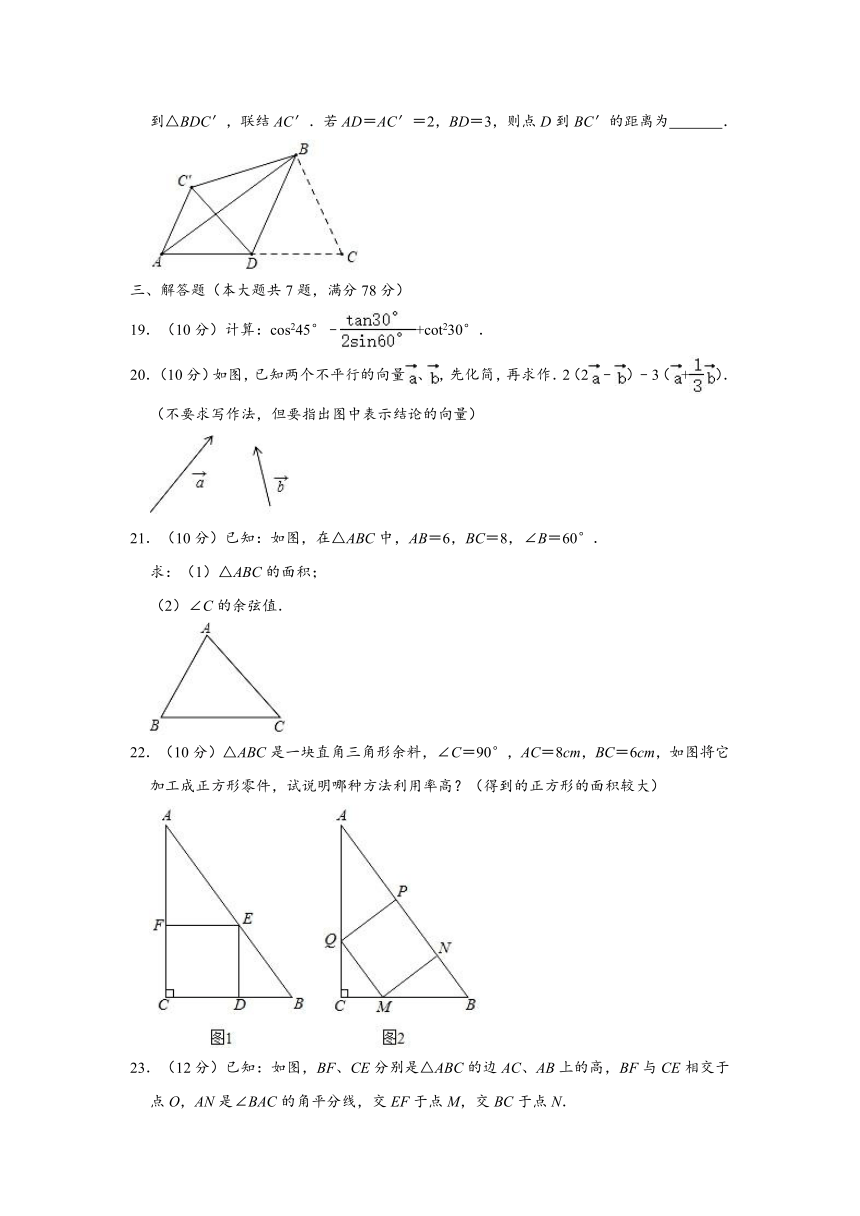
3.(4分)在Rt△ABC中,∠C=90°,AC=12,BC=5,那么下列各式中正确的是( )
A.tanA= B.cotA= C.sinA= D.cosA=
4.(4分)已知△ABC中,D、E分别是边AB、AC上的点,下列各式中,不能判断DE∥BC的是( )
A.= B.= C.= D.=
5.(4分)已知、和都是非零向量,在下列选项中,不能判定∥的是( )
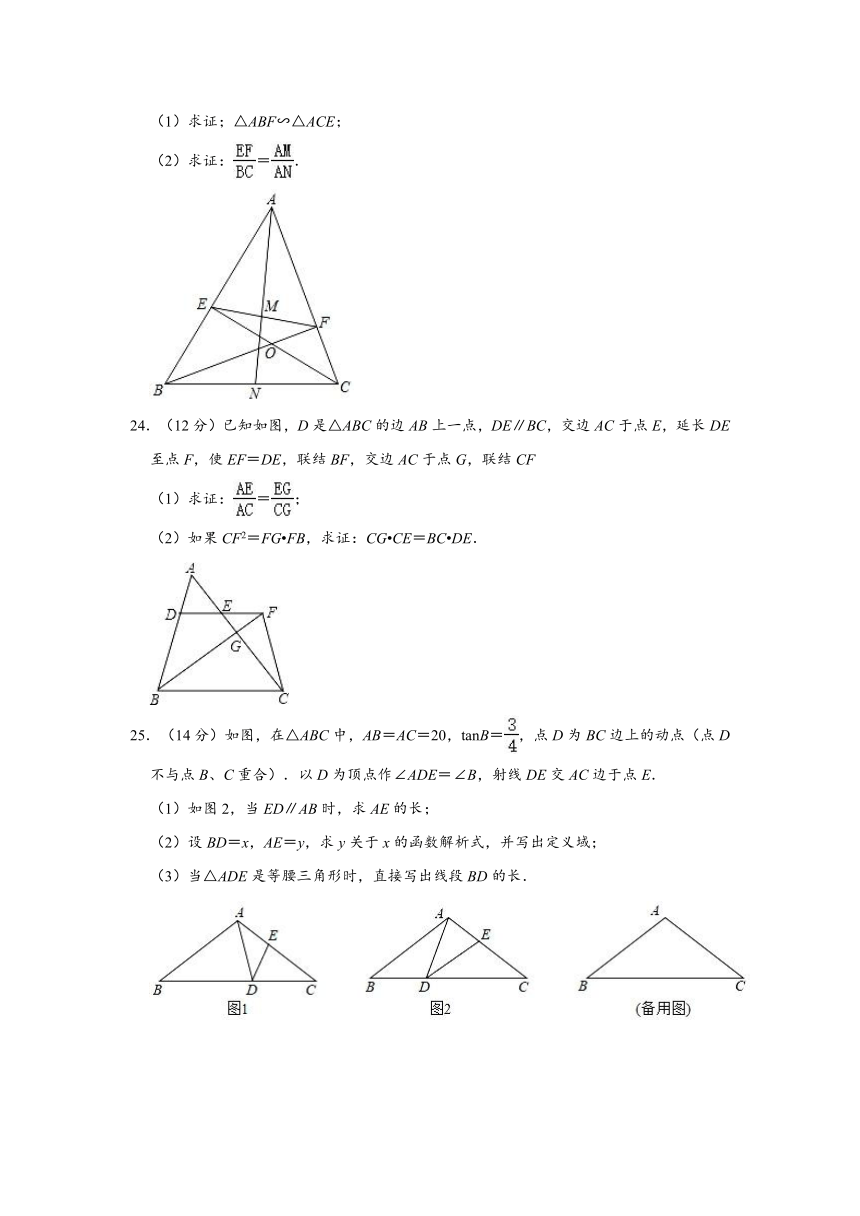
A.=2 B.∥,∥ C.||=|| D.=,=2
6.(4分)如图,在梯形ABCD中,AD∥BC,BC=2AD,对角线AC与BD相交于点O,把△ABO、△BCO、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确( ).
A.S2=2S1 B.S1=S3 C.S2=2S4 D.S3=2S4
二、填空题(共12题,每题4分,满分48分)
7.(4分)若==≠0,则= .
8.(4分)在比例尺为1:1000000的地图上,量得两地间的距离为3厘米,那么两地间的实际距离是 千米.
9.(4分)已知两相似三角形的对应中线的比是2:3,其中较大的三角形的面积为27,则较小的三角形的面积是 .
10.(4分)如果线段a=4cm,b=9cm,那么它们的比例中项是 cm.
11.(4分)已知点M是线段AB的黄金分割点(AM>MB),如果AB=6cm,那么AM= cm.
12.(4分)如图,G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,若BC=6,则EF= .
13.(4分)如图,梯形ABCD中,点E、F分别在AB、DC边上,AD∥BC∥EF,BE:EA=1:2,若FC=2.5,则FD= .
14.(4分)在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE:BC=1:3,AD=2,则BD= .
15.(4分)在平面直角坐标系xOy中有一点A(3,4),如果OA与x轴正半轴的夹角为α,那么sinα= .
16.(4分)如图,已知在△ABC中,∠ABD=∠C,AD=9,CD=7,那么AB= .
17.(4分)如图,在平行四边形ABCD中,点F是CD的中点,BF和AC交于点E.如果=,=,如果用、表示,那么= .
18.(4分)如图,在△ABC中,D是AC边的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,联结AC′.若AD=AC′=2,BD=3,则点D到BC′的距离为 .
三、解答题(本大题共7题,满分78分)
19.(10分)计算:cos245°﹣+cot230°.
20.(10分)如图,已知两个不平行的向量、,先化简,再求作.2(2﹣)﹣3(+).
(不要求写作法,但要指出图中表示结论的向量)
21.(10分)已知:如图,在△ABC中,AB=6,BC=8,∠B=60°.
求:(1)△ABC的面积;
(2)∠C的余弦值.
22.(10分)△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
23.(12分)已知:如图,BF、CE分别是△ABC的边AC、AB上的高,BF与CE相交于点O,AN是∠BAC的角平分线,交EF于点M,交BC于点N.
(1)求证;△ABF∽△ACE;
(2)求证:=.
24.(12分)已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,联结BF,交边AC于点G,联结CF
(1)求证:=;
(2)如果CF2=FG?FB,求证:CG?CE=BC?DE.
25.(14分)如图,在△ABC中,AB=AC=20,tanB=,点D为BC边上的动点(点D不与点B、C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E.
(1)如图2,当ED∥AB时,求AE的长;
(2)设BD=x,AE=y,求y关于x的函数解析式,并写出定义域;
(3)当△ADE是等腰三角形时,直接写出线段BD的长.
参考答案
一、选择题(共6小题).
1.(4分)下列各组线段中,能组成比例线段的( )
A.2,3,4,5 B.2,3,4,6 C.2,3,5,7 D.3,4,5,6
解:A、2×5≠3×4,不成比例;
B、2×6=3×4,成比例;
C、2×7≠3×5,不成比例;
D、3×6≠4×5,不成比例;
故选:B.
2.(4分)下列图形中一定相似的是( )
A.两个等腰三角形 B.两个菱形
C.两个直角三角形 D.两个正方形
解:A、两个等腰三角形,属于形状不唯一确定的图形,不一定相似,故错误;
B、两个菱形,属于形状不唯一确定的图形,不一定相似,故错误;
C、两个直角三角形,属于形状不唯一确定的图形,不一定相似,故错误;
D、两个正方形,图形的形状相同,但大小不一定相同,符合相似性的定义,故正确.
故选:D.
3.(4分)在Rt△ABC中,∠C=90°,AC=12,BC=5,那么下列各式中正确的是( )
A.tanA= B.cotA= C.sinA= D.cosA=
解:在Rt△ABC中,∠C=90°,AC=12,BC=5,
由勾股定理得,AB==13,
则tanA==,A选项计算正确;
cotA==,B选项计算错误;
sinA==,C选项计算错误;
cosA==,D选项计算错误;
故选:A.
4.(4分)已知△ABC中,D、E分别是边AB、AC上的点,下列各式中,不能判断DE∥BC的是( )
A.= B.= C.= D.=
解:如图,若使线段DE∥BC,则其对应边必成比例,
即=,=,=,
故B选项答案错误;
故选:B.
5.(4分)已知、和都是非零向量,在下列选项中,不能判定∥的是( )
A.=2 B.∥,∥ C.||=|| D.=,=2
解:A、由=2,可以推出∥.本选项不符合题意;
B、由∥,∥,可以推出∥.本选项不符合题意;
C、由||=||,不可以推出∥.本选项符合题意;
D、由=,=2,可以推出∥.本选项不符合题意;
故选:C.
6.(4分)如图,在梯形ABCD中,AD∥BC,BC=2AD,对角线AC与BD相交于点O,把△ABO、△BCO、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确( ).
A.S2=2S1 B.S1=S3 C.S2=2S4 D.S3=2S4
解:∵AD∥BC,
∴△AOD∽△COB,
∴===,
∴S△BOC=2S△AOB=2S△ODC,S△DOC=2S△AOD,=()2=,
∴选项A,B,D正确,
故选:C.
二、填空题(本大题共12题,每题4分,满分48分)
7.(4分)若==≠0,则= .
解:设===k≠0,则x=2k,y=5k,z=4k,
则==;
故答案为:.
8.(4分)在比例尺为1:1000000的地图上,量得两地间的距离为3厘米,那么两地间的实际距离是 30 千米.
解:根据题意,3÷=3000 000厘米=30千米.
即实际距离是30千米.
故答案为:30.
9.(4分)已知两相似三角形的对应中线的比是2:3,其中较大的三角形的面积为27,则较小的三角形的面积是 12 .
解:∵两相似三角形的对应中线的比是2:3,
∴两相似三角形的相似比是2:3,
∴两相似三角形的面积比是4:9,
∵较大的三角形的面积为27,
∴较小的三角形的面积为:27×=12,
故答案为:12.
10.(4分)如果线段a=4cm,b=9cm,那么它们的比例中项是 6 cm.
解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
所以c2=4×9,x=±6,(线段是正数,负值舍去),
故答案为:6.
11.(4分)已知点M是线段AB的黄金分割点(AM>MB),如果AB=6cm,那么AM= (3﹣3) cm.
解:∵M是线段AB的黄金分割点(AM>MB),AB=6cm,
∴AM=AB=×6=(3﹣3)cm,
故答案为:(3﹣3).
12.(4分)如图,G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,若BC=6,则EF= 4 .
解:如图,连接AG并延长,交BC于点P.
∵G为△ABC的重心,
∴AG=2GP,
∴AG:AP=2:3,
∵EF过点G且EF∥BC,
∴△AGF∽△APC,
∴AF:AC=AG:AP=2:3,
又∵EF∥BC,
∴△AEF∽△ABC,
∴,
∵BC=6,
∴EF=4.
13.(4分)如图,梯形ABCD中,点E、F分别在AB、DC边上,AD∥BC∥EF,BE:EA=1:2,若FC=2.5,则FD= 5 .
解:∵AD∥BC∥EF,BE:EA=1:2,
∴FC:FD=1:2,
∵FC=2.5,
∴FD=5.
故答案为5.
14.(4分)在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE:BC=1:3,AD=2,则BD= 4 .
解:依题意画出图形,如图:
在△ABC中,DE∥BC,
∴△ADE∽△ABC,
∴=,
∵DE:BC=1:3,
∴=,
∵AD=2,
∴AB=6,
∴BD=AB﹣AD=6﹣2=4.
故答案为:4.
15.(4分)在平面直角坐标系xOy中有一点A(3,4),如果OA与x轴正半轴的夹角为α,那么sinα= .
解:∵A(3,4),
∴OA==5,
∴sinα=.
故答案为:.
16.(4分)如图,已知在△ABC中,∠ABD=∠C,AD=9,CD=7,那么AB= 12 .
解:∵在△ABC中,∠ABD=∠C,
而∠A公共,
∴△ABD∽△ACB,
∴AB2=AD?AC,
而AD=9,CD=7,
∴AC=16,
∴AB=12.
17.(4分)如图,在平行四边形ABCD中,点F是CD的中点,BF和AC交于点E.如果=,=,如果用、表示,那么= (+) .
解:∵点F是CD的中点,
∴FC=DC.
又∵在平行四边形ABCD中,CD∥AB,CD=AB,
∴=,即==,
∴AE=AC.
∵=,=,
∴=+=+,
∴==(+),
故答案是:(+).
18.(4分)如图,在△ABC中,D是AC边的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,联结AC′.若AD=AC′=2,BD=3,则点D到BC′的距离为 .
解:如图,连接CC',交BD于点M,过点D作DH⊥BC'于点H,
∵AD=AC′=2,D是AC边上的中点,
∴DC=AD=2,
由翻折知,△BDC≌△BDC',BD垂直平分CC',
∴DC=DC'=2,BC=BC',CM=C'M,
∴AD=AC′=DC'=2,
∴△ADC'为等边三角形,
∴∠ADC'=∠AC'D=∠C'AC=60°,
∵DC=DC',
∴∠DCC'=∠DC'C=×60°=30°,
在Rt△C'DM中,
∠DC'C=30°,DC'=2,
∴DM=1,C'M=DM=,
∴BM=BD﹣DM=3﹣1=2,
在Rt△BMC'中,
BC'===,
∵S△BDC'=BC'?DH=BD?CM,
∴DH=3×,
∴DH=,
∵∠DCB=∠DBC',
∴点D到BC的距离为.
故答案为:.
三、解答题(本大题共7题,满分78分)
19.(10分)计算:cos245°﹣+cot230°.
解:原式=()2﹣+()2
=﹣+3
=.
20.(10分)如图,已知两个不平行的向量、,先化简,再求作.2(2﹣)﹣3(+).
(不要求写作法,但要指出图中表示结论的向量)
解:2(2﹣)﹣3(+)
=4﹣2﹣3﹣
=﹣3.
如图,即为所求.
21.(10分)已知:如图,在△ABC中,AB=6,BC=8,∠B=60°.
求:(1)△ABC的面积;
(2)∠C的余弦值.
解:(1)作AD⊥BC于点D,
∵在△ABC中,AB=6,BC=8,∠B=60°,
∴∠ADB=90°,∠BAD=30°,
∴BD=3,
∴AD=3,
∴△ABC的面积是:;
(2)由(1)知∠ADC=90°,BD=3,AD=3,
∵BC=8,
∴CD=5,
∴AC=2,
∴cos∠C=.
22.(10分)△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
解:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则DE=xcm,BD=BC﹣CD=(6﹣x)cm,
∵DE∥AC,
∴△BDE∽△BCA,
∴=,即=,
解得:x=(cm),
即正方形BDEF边长为cm;
当所截的正方形的边在△ABC的斜边上,如图2,作CH⊥AB于H,交MQ于J,
则MN∥CH,
AB===10,
∵CH?AB=AC?BC
∴CH==(cm),
设正方形MNPQ边长为x,则QM=x,BJ=﹣x,
∵QM∥AB,
∴△CMQ∽△CBA,
∴=,即=,
解得:x=(cm),
即正方形BDEF边长为(cm);
∵=>,
∴图1利用率高.
23.(12分)已知:如图,BF、CE分别是△ABC的边AC、AB上的高,BF与CE相交于点O,AN是∠BAC的角平分线,交EF于点M,交BC于点N.
(1)求证;△ABF∽△ACE;
(2)求证:=.
解:(1)证明:∵BF、CE分别是△ABC的边AC、AB上的高,
∴BF⊥AC,CE⊥AB,
∴∠AFB=∠AEC=90°,
又∵∠CAE=∠BAF,
∴△ABF∽△ACE;
(2)证明:∵△ABF∽△ACE,
∴=,
∴=,
又∵∠EAF=∠CAB,
∴△EAF∽△CAB,
∴=①,∠AEF=∠ACB,
∵AN是∠BAC的角平分线,
∴∠EAM=∠CAN,
∴△EAM∽△CAN,
∴=②,
由①②可得:
=.
24.(12分)已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,联结BF,交边AC于点G,联结CF
(1)求证:=;
(2)如果CF2=FG?FB,求证:CG?CE=BC?DE.
【解答】证明:(1)∵DE∥BC,
∴△ADE∽△ABC,△EFG∽△CBG,
∴=,=,
又∵DE=EF,
∴=,
∴=;
(2)∵CF2=FG?FB,
∴=,
又∵∠CFG=∠CFB,
∴△CFG∽△BFC,
∴=,∠FCE=∠CBF,
又∵DF∥BC,
∴∠EFG=∠CBF,
∴∠FCE=∠EFG,
又∵∠FEG=∠CEF,
∴△EFG∽△ECF,
∴==,
∴=,即CG?CE=BC?DE.
25.(14分)如图,在△ABC中,AB=AC=20,tanB=,点D为BC边上的动点(点D不与点B、C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E.
(1)如图2,当ED∥AB时,求AE的长;
(2)设BD=x,AE=y,求y关于x的函数解析式,并写出定义域;
(3)当△ADE是等腰三角形时,直接写出线段BD的长.
解:(1)如图1,故点A作AH⊥BC于点H,
在Rt△ABH中,设tanB==tanα,则sinα=,cosα=,
则AH=ABsinα=20×=12,BH=16,则BC=2BH=32,
∵ED∥AB,则∠ADE=∠BAD=∠B=α,
则△ABD为等腰三角形,
在△ABD中,过点D作DM⊥AB于点M,
则MD=BDsinB,BM=BDcosB=AB,
即BD=AB=×20,解得BD=,
∵DE∥BA,则,即,
解得:AE=;
(2)如图2,
在△ABD中,∠ADC=∠ADE+∠EDC=∠BAD+∠B,
∵∠ADE=∠B,
∴∠EDC=∠BAD,
∴△ABD∽△DCE,则,
其中,AB=20,CD=32﹣x,BD=x,CE=20﹣y,
故,
化简得:y=x2﹣x+20(0<x<32);
(3)①当AD=DE时,此时点B、D重合,不符合题意;
②当AD=DE时,
由(2)知则=1,即=1,
解得x=12,即BD=12;
③当AE=DE时,
∵AE=DE,
∴∠DAE=∠ADE=∠C,
故△ADC为等腰三角形,
则AD=CD=32﹣x,
在△ABD中,BD=x,AD=32﹣x,如图1,
则AH=12,AH=16,
在△ADH中,AD=32﹣x,DH=16﹣x,AH=12,
由勾股定理得:(32﹣x)2=(16﹣x)2+122,
解得x=19.5;
综上,BD的长度为12或19.5.
一、选择题(共6小题).
1.(4分)下列各组线段中,能组成比例线段的( )
A.2,3,4,5 B.2,3,4,6 C.2,3,5,7 D.3,4,5,6
2.(4分)下列图形中一定相似的是( )
A.两个等腰三角形 B.两个菱形
C.两个直角三角形 D.两个正方形
3.(4分)在Rt△ABC中,∠C=90°,AC=12,BC=5,那么下列各式中正确的是( )
A.tanA= B.cotA= C.sinA= D.cosA=
4.(4分)已知△ABC中,D、E分别是边AB、AC上的点,下列各式中,不能判断DE∥BC的是( )
A.= B.= C.= D.=
5.(4分)已知、和都是非零向量,在下列选项中,不能判定∥的是( )
A.=2 B.∥,∥ C.||=|| D.=,=2
6.(4分)如图,在梯形ABCD中,AD∥BC,BC=2AD,对角线AC与BD相交于点O,把△ABO、△BCO、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确( ).
A.S2=2S1 B.S1=S3 C.S2=2S4 D.S3=2S4
二、填空题(共12题,每题4分,满分48分)
7.(4分)若==≠0,则= .
8.(4分)在比例尺为1:1000000的地图上,量得两地间的距离为3厘米,那么两地间的实际距离是 千米.
9.(4分)已知两相似三角形的对应中线的比是2:3,其中较大的三角形的面积为27,则较小的三角形的面积是 .
10.(4分)如果线段a=4cm,b=9cm,那么它们的比例中项是 cm.
11.(4分)已知点M是线段AB的黄金分割点(AM>MB),如果AB=6cm,那么AM= cm.
12.(4分)如图,G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,若BC=6,则EF= .
13.(4分)如图,梯形ABCD中,点E、F分别在AB、DC边上,AD∥BC∥EF,BE:EA=1:2,若FC=2.5,则FD= .
14.(4分)在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE:BC=1:3,AD=2,则BD= .
15.(4分)在平面直角坐标系xOy中有一点A(3,4),如果OA与x轴正半轴的夹角为α,那么sinα= .
16.(4分)如图,已知在△ABC中,∠ABD=∠C,AD=9,CD=7,那么AB= .
17.(4分)如图,在平行四边形ABCD中,点F是CD的中点,BF和AC交于点E.如果=,=,如果用、表示,那么= .
18.(4分)如图,在△ABC中,D是AC边的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,联结AC′.若AD=AC′=2,BD=3,则点D到BC′的距离为 .
三、解答题(本大题共7题,满分78分)
19.(10分)计算:cos245°﹣+cot230°.
20.(10分)如图,已知两个不平行的向量、,先化简,再求作.2(2﹣)﹣3(+).
(不要求写作法,但要指出图中表示结论的向量)
21.(10分)已知:如图,在△ABC中,AB=6,BC=8,∠B=60°.
求:(1)△ABC的面积;
(2)∠C的余弦值.
22.(10分)△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
23.(12分)已知:如图,BF、CE分别是△ABC的边AC、AB上的高,BF与CE相交于点O,AN是∠BAC的角平分线,交EF于点M,交BC于点N.
(1)求证;△ABF∽△ACE;
(2)求证:=.
24.(12分)已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,联结BF,交边AC于点G,联结CF
(1)求证:=;
(2)如果CF2=FG?FB,求证:CG?CE=BC?DE.
25.(14分)如图,在△ABC中,AB=AC=20,tanB=,点D为BC边上的动点(点D不与点B、C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E.
(1)如图2,当ED∥AB时,求AE的长;
(2)设BD=x,AE=y,求y关于x的函数解析式,并写出定义域;
(3)当△ADE是等腰三角形时,直接写出线段BD的长.
参考答案
一、选择题(共6小题).
1.(4分)下列各组线段中,能组成比例线段的( )
A.2,3,4,5 B.2,3,4,6 C.2,3,5,7 D.3,4,5,6
解:A、2×5≠3×4,不成比例;
B、2×6=3×4,成比例;
C、2×7≠3×5,不成比例;
D、3×6≠4×5,不成比例;
故选:B.
2.(4分)下列图形中一定相似的是( )
A.两个等腰三角形 B.两个菱形
C.两个直角三角形 D.两个正方形
解:A、两个等腰三角形,属于形状不唯一确定的图形,不一定相似,故错误;
B、两个菱形,属于形状不唯一确定的图形,不一定相似,故错误;
C、两个直角三角形,属于形状不唯一确定的图形,不一定相似,故错误;
D、两个正方形,图形的形状相同,但大小不一定相同,符合相似性的定义,故正确.
故选:D.
3.(4分)在Rt△ABC中,∠C=90°,AC=12,BC=5,那么下列各式中正确的是( )
A.tanA= B.cotA= C.sinA= D.cosA=
解:在Rt△ABC中,∠C=90°,AC=12,BC=5,
由勾股定理得,AB==13,
则tanA==,A选项计算正确;
cotA==,B选项计算错误;
sinA==,C选项计算错误;
cosA==,D选项计算错误;
故选:A.
4.(4分)已知△ABC中,D、E分别是边AB、AC上的点,下列各式中,不能判断DE∥BC的是( )
A.= B.= C.= D.=
解:如图,若使线段DE∥BC,则其对应边必成比例,
即=,=,=,
故B选项答案错误;
故选:B.
5.(4分)已知、和都是非零向量,在下列选项中,不能判定∥的是( )
A.=2 B.∥,∥ C.||=|| D.=,=2
解:A、由=2,可以推出∥.本选项不符合题意;
B、由∥,∥,可以推出∥.本选项不符合题意;
C、由||=||,不可以推出∥.本选项符合题意;
D、由=,=2,可以推出∥.本选项不符合题意;
故选:C.
6.(4分)如图,在梯形ABCD中,AD∥BC,BC=2AD,对角线AC与BD相交于点O,把△ABO、△BCO、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确( ).
A.S2=2S1 B.S1=S3 C.S2=2S4 D.S3=2S4
解:∵AD∥BC,
∴△AOD∽△COB,
∴===,
∴S△BOC=2S△AOB=2S△ODC,S△DOC=2S△AOD,=()2=,
∴选项A,B,D正确,
故选:C.
二、填空题(本大题共12题,每题4分,满分48分)
7.(4分)若==≠0,则= .
解:设===k≠0,则x=2k,y=5k,z=4k,
则==;
故答案为:.
8.(4分)在比例尺为1:1000000的地图上,量得两地间的距离为3厘米,那么两地间的实际距离是 30 千米.
解:根据题意,3÷=3000 000厘米=30千米.
即实际距离是30千米.
故答案为:30.
9.(4分)已知两相似三角形的对应中线的比是2:3,其中较大的三角形的面积为27,则较小的三角形的面积是 12 .
解:∵两相似三角形的对应中线的比是2:3,
∴两相似三角形的相似比是2:3,
∴两相似三角形的面积比是4:9,
∵较大的三角形的面积为27,
∴较小的三角形的面积为:27×=12,
故答案为:12.
10.(4分)如果线段a=4cm,b=9cm,那么它们的比例中项是 6 cm.
解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
所以c2=4×9,x=±6,(线段是正数,负值舍去),
故答案为:6.
11.(4分)已知点M是线段AB的黄金分割点(AM>MB),如果AB=6cm,那么AM= (3﹣3) cm.
解:∵M是线段AB的黄金分割点(AM>MB),AB=6cm,
∴AM=AB=×6=(3﹣3)cm,
故答案为:(3﹣3).
12.(4分)如图,G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,若BC=6,则EF= 4 .
解:如图,连接AG并延长,交BC于点P.
∵G为△ABC的重心,
∴AG=2GP,
∴AG:AP=2:3,
∵EF过点G且EF∥BC,
∴△AGF∽△APC,
∴AF:AC=AG:AP=2:3,
又∵EF∥BC,
∴△AEF∽△ABC,
∴,
∵BC=6,
∴EF=4.
13.(4分)如图,梯形ABCD中,点E、F分别在AB、DC边上,AD∥BC∥EF,BE:EA=1:2,若FC=2.5,则FD= 5 .
解:∵AD∥BC∥EF,BE:EA=1:2,
∴FC:FD=1:2,
∵FC=2.5,
∴FD=5.
故答案为5.
14.(4分)在△ABC中,点D、E分别在边AB、AC上,DE∥BC,DE:BC=1:3,AD=2,则BD= 4 .
解:依题意画出图形,如图:
在△ABC中,DE∥BC,
∴△ADE∽△ABC,
∴=,
∵DE:BC=1:3,
∴=,
∵AD=2,
∴AB=6,
∴BD=AB﹣AD=6﹣2=4.
故答案为:4.
15.(4分)在平面直角坐标系xOy中有一点A(3,4),如果OA与x轴正半轴的夹角为α,那么sinα= .
解:∵A(3,4),
∴OA==5,
∴sinα=.
故答案为:.
16.(4分)如图,已知在△ABC中,∠ABD=∠C,AD=9,CD=7,那么AB= 12 .
解:∵在△ABC中,∠ABD=∠C,
而∠A公共,
∴△ABD∽△ACB,
∴AB2=AD?AC,
而AD=9,CD=7,
∴AC=16,
∴AB=12.
17.(4分)如图,在平行四边形ABCD中,点F是CD的中点,BF和AC交于点E.如果=,=,如果用、表示,那么= (+) .
解:∵点F是CD的中点,
∴FC=DC.
又∵在平行四边形ABCD中,CD∥AB,CD=AB,
∴=,即==,
∴AE=AC.
∵=,=,
∴=+=+,
∴==(+),
故答案是:(+).
18.(4分)如图,在△ABC中,D是AC边的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,联结AC′.若AD=AC′=2,BD=3,则点D到BC′的距离为 .
解:如图,连接CC',交BD于点M,过点D作DH⊥BC'于点H,
∵AD=AC′=2,D是AC边上的中点,
∴DC=AD=2,
由翻折知,△BDC≌△BDC',BD垂直平分CC',
∴DC=DC'=2,BC=BC',CM=C'M,
∴AD=AC′=DC'=2,
∴△ADC'为等边三角形,
∴∠ADC'=∠AC'D=∠C'AC=60°,
∵DC=DC',
∴∠DCC'=∠DC'C=×60°=30°,
在Rt△C'DM中,
∠DC'C=30°,DC'=2,
∴DM=1,C'M=DM=,
∴BM=BD﹣DM=3﹣1=2,
在Rt△BMC'中,
BC'===,
∵S△BDC'=BC'?DH=BD?CM,
∴DH=3×,
∴DH=,
∵∠DCB=∠DBC',
∴点D到BC的距离为.
故答案为:.
三、解答题(本大题共7题,满分78分)
19.(10分)计算:cos245°﹣+cot230°.
解:原式=()2﹣+()2
=﹣+3
=.
20.(10分)如图,已知两个不平行的向量、,先化简,再求作.2(2﹣)﹣3(+).
(不要求写作法,但要指出图中表示结论的向量)
解:2(2﹣)﹣3(+)
=4﹣2﹣3﹣
=﹣3.
如图,即为所求.
21.(10分)已知:如图,在△ABC中,AB=6,BC=8,∠B=60°.
求:(1)△ABC的面积;
(2)∠C的余弦值.
解:(1)作AD⊥BC于点D,
∵在△ABC中,AB=6,BC=8,∠B=60°,
∴∠ADB=90°,∠BAD=30°,
∴BD=3,
∴AD=3,
∴△ABC的面积是:;
(2)由(1)知∠ADC=90°,BD=3,AD=3,
∵BC=8,
∴CD=5,
∴AC=2,
∴cos∠C=.
22.(10分)△ABC是一块直角三角形余料,∠C=90°,AC=8cm,BC=6cm,如图将它加工成正方形零件,试说明哪种方法利用率高?(得到的正方形的面积较大)
解:当所截的正方形的边在△ABC的直角边上,如图1,设正方形CDEF边长为x,则DE=xcm,BD=BC﹣CD=(6﹣x)cm,
∵DE∥AC,
∴△BDE∽△BCA,
∴=,即=,
解得:x=(cm),
即正方形BDEF边长为cm;
当所截的正方形的边在△ABC的斜边上,如图2,作CH⊥AB于H,交MQ于J,
则MN∥CH,
AB===10,
∵CH?AB=AC?BC
∴CH==(cm),
设正方形MNPQ边长为x,则QM=x,BJ=﹣x,
∵QM∥AB,
∴△CMQ∽△CBA,
∴=,即=,
解得:x=(cm),
即正方形BDEF边长为(cm);
∵=>,
∴图1利用率高.
23.(12分)已知:如图,BF、CE分别是△ABC的边AC、AB上的高,BF与CE相交于点O,AN是∠BAC的角平分线,交EF于点M,交BC于点N.
(1)求证;△ABF∽△ACE;
(2)求证:=.
解:(1)证明:∵BF、CE分别是△ABC的边AC、AB上的高,
∴BF⊥AC,CE⊥AB,
∴∠AFB=∠AEC=90°,
又∵∠CAE=∠BAF,
∴△ABF∽△ACE;
(2)证明:∵△ABF∽△ACE,
∴=,
∴=,
又∵∠EAF=∠CAB,
∴△EAF∽△CAB,
∴=①,∠AEF=∠ACB,
∵AN是∠BAC的角平分线,
∴∠EAM=∠CAN,
∴△EAM∽△CAN,
∴=②,
由①②可得:
=.
24.(12分)已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,联结BF,交边AC于点G,联结CF
(1)求证:=;
(2)如果CF2=FG?FB,求证:CG?CE=BC?DE.
【解答】证明:(1)∵DE∥BC,
∴△ADE∽△ABC,△EFG∽△CBG,
∴=,=,
又∵DE=EF,
∴=,
∴=;
(2)∵CF2=FG?FB,
∴=,
又∵∠CFG=∠CFB,
∴△CFG∽△BFC,
∴=,∠FCE=∠CBF,
又∵DF∥BC,
∴∠EFG=∠CBF,
∴∠FCE=∠EFG,
又∵∠FEG=∠CEF,
∴△EFG∽△ECF,
∴==,
∴=,即CG?CE=BC?DE.
25.(14分)如图,在△ABC中,AB=AC=20,tanB=,点D为BC边上的动点(点D不与点B、C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E.
(1)如图2,当ED∥AB时,求AE的长;
(2)设BD=x,AE=y,求y关于x的函数解析式,并写出定义域;
(3)当△ADE是等腰三角形时,直接写出线段BD的长.
解:(1)如图1,故点A作AH⊥BC于点H,
在Rt△ABH中,设tanB==tanα,则sinα=,cosα=,
则AH=ABsinα=20×=12,BH=16,则BC=2BH=32,
∵ED∥AB,则∠ADE=∠BAD=∠B=α,
则△ABD为等腰三角形,
在△ABD中,过点D作DM⊥AB于点M,
则MD=BDsinB,BM=BDcosB=AB,
即BD=AB=×20,解得BD=,
∵DE∥BA,则,即,
解得:AE=;
(2)如图2,
在△ABD中,∠ADC=∠ADE+∠EDC=∠BAD+∠B,
∵∠ADE=∠B,
∴∠EDC=∠BAD,
∴△ABD∽△DCE,则,
其中,AB=20,CD=32﹣x,BD=x,CE=20﹣y,
故,
化简得:y=x2﹣x+20(0<x<32);
(3)①当AD=DE时,此时点B、D重合,不符合题意;
②当AD=DE时,
由(2)知则=1,即=1,
解得x=12,即BD=12;
③当AE=DE时,
∵AE=DE,
∴∠DAE=∠ADE=∠C,
故△ADC为等腰三角形,
则AD=CD=32﹣x,
在△ABD中,BD=x,AD=32﹣x,如图1,
则AH=12,AH=16,
在△ADH中,AD=32﹣x,DH=16﹣x,AH=12,
由勾股定理得:(32﹣x)2=(16﹣x)2+122,
解得x=19.5;
综上,BD的长度为12或19.5.
同课章节目录
