福建省莆田市六校2020-2021学年八年级上学期期中考试数学试卷(Word版含答案)
文档属性
| 名称 | 福建省莆田市六校2020-2021学年八年级上学期期中考试数学试卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 330.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 21:28:57 | ||
图片预览



文档简介
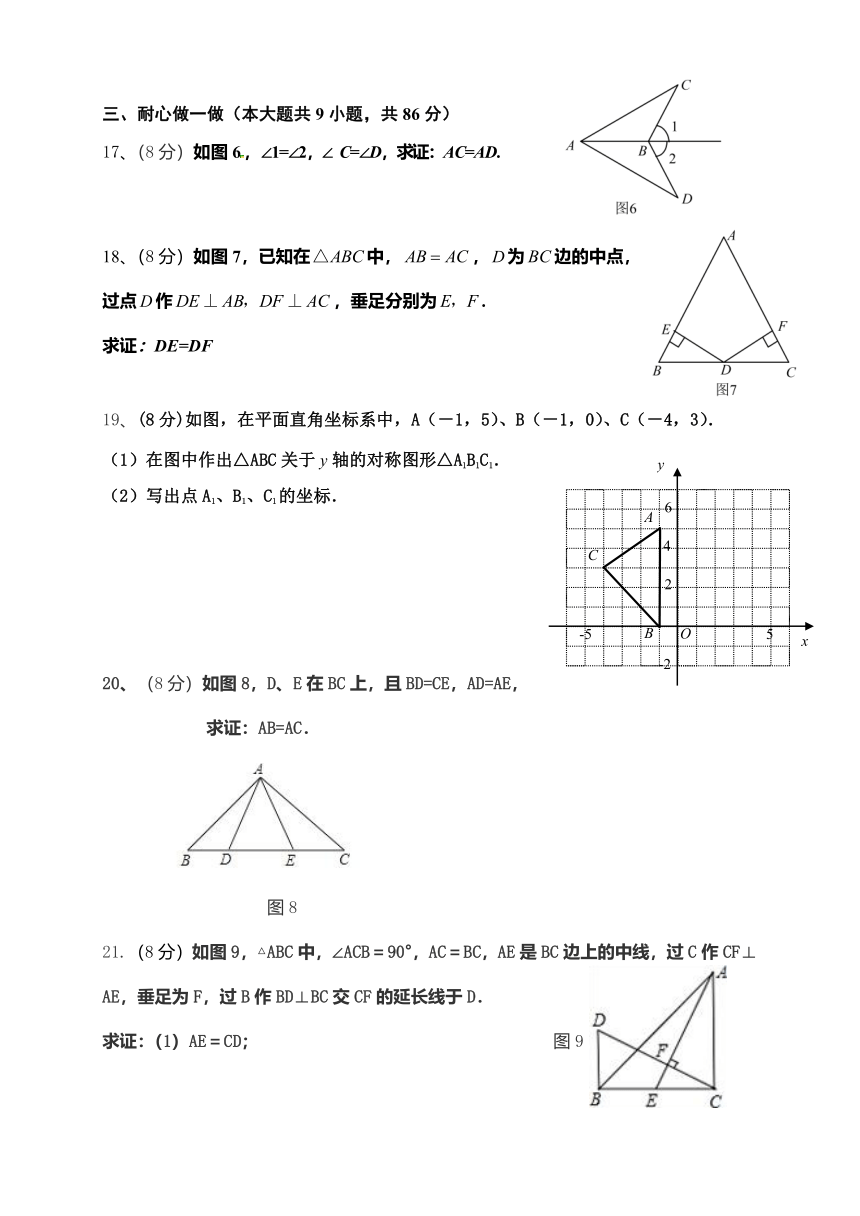
2020-2021学年第一学期第六联盟校期中联考
八年级数学科试卷
总分:150分
考试时间:120分钟
一、精心选一选,选择题:(每题只有一个正确答案,每小题4分,共40分)
1.日常生活中,我们会看到很多标志,在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A.
B.
C.
D.
2.以下列各组线段为边,能组成三角形的是(
)
A.2cm,3cm,5cm
B.5cm,6cm,10cm
C.1cm,1cm,3cm
D.3cm,4cm,9cm
3.下面四个图形中,线段BE是△ABC的高的图是(
)
A.
B.
C.
D.
4.已知△ABC≌△DEF,且AB=4,BC=5,AC=6,则DE的长为(
)
A.4
B.5
C.6
D.不能确定
5.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的(
)
A.AB=CD
B.EC=BF
C.∠A=∠D
D.AB=BC
6.等腰三角形的两边长分别为4cm和8cm,则它的周长为(
)
A.16cm
B.17cm
C.20cm
D.16cm或20cm
7.能把一个三角形分成两个面积相等的三角形是三角形的(
)
A.中线
B.高线
C.角平分线
D.以上都不对
8.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
9.如图,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2=(
)
A.360°
B.180°
C.255°
D.145°
10.如图:BO、CO是∠ABC,∠ACB的两条角平分线,∠A=100°,则∠BOC的度数为(
)
A.80°
B.90°
C.120°
D.140°
二、细心填一填:本大题共6小题,每小题4分,共24分.
11.如图,,,与关于直线l对称,则∠B=
.
11题图
13题图
14题图
12.若正n边形的一个外角为45°,则n=__________.
13.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5.则△BEC的周长是____.
14.如图所示,某同学将一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻
璃,那么最省事的办法是带第__________块去.(填序号)
15.如图所示,在△ABC中,∠BAC=130°,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F,则∠MAN为________.
15题图
16.如图,在中,平分交于点,点分别是和上的动点,当,时,的最小值等于__________.
16题图
三、耐心做一做(本大题共9小题,共86分)
17、(8分)如图6,∠1=∠2,∠
C=∠D,求证:AC=AD.
18、(8分)如图7,已知在中,,为边的中点,
过点作,垂足分别为.
求证:DE=DF
19、(8分)如图,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3).
(1)在图中作出△ABC关于轴的对称图形△A1B1C1.
(2)写出点A1、B1、C1的坐标.
(8分)如图8,D、E在BC上,且BD=CE,AD=AE,
求证:AB=AC.
图8
21.(8分)如图9,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.?
求证:(1)AE=CD;
图9
(2)若AC=12,求BD的长
22、(10分)如图10所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
图10
(12分)如图11所示在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?
并证明你的结论.
图11
24.(本题12分)如图,在△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE,点E在BC上.过点D作DF∥BC,连接DB.
求证:(1)△ABD≌△ACE;
DF=CE.
(本题12分)如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,
动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
(1)求证:AF=AM;
(2)当t取何值时,△DFE与△DMG全等;
(3)求证:在运动过程中,不管t取何值,都有
2020-2021学年上学期八年级数学期中联考(答案)
一、选择题(每小题4分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
D
A
A
C
A
B
C
D
二、填空题(每小题4分,共24分)
11、
12、
8
13、
13
14、③
15、
16、3
三、解答题(共86分)
17、证明:∵∠1=∠2,
∴∠ABC=∠ABD,在△ABD和△ABC中,…………(2分),
∵∠ABC=∠ABD
∠
C=∠D
AB=AB
∴△ABD≌△ABC(AAS),…………(6分)
∴AD=AC.
…………(8分)
证明:连接AD,∵AB=AC,D为BC的中点,
∴BD=DC,在△ABD和△ACD中,
AB=AC,BD=DC,AD=AD
∴△ABD≌△ACD(SSS)…………(3分),
∴∠BAD=∠CAD
,…………(4分)
∵…………(6分)
∴DE=DF.
…………(8分)
法2:也可以先证明△ABD≌△ACD(SSS)…(3分)再证明△ADE≌△ADF(AAS)(3分)
法3:∵AB=AC,
∴∠B=∠C,D为BC的中点,
∴BD=DC
∠BED=∠CFD…(3分),
在△BDE和△CDF中
∠B=∠C
∠BED=∠CFD
BD=DC
∴△BDE≌△CDF(AAS)(6分)
∴DE=DF.
…………(8分)
19、(1)作图
(略)…(4分),(2)A1(1,5)B1(1,0)
C1(4,3)…(4分),
20、(8分)证明:∵∠ADE=∠AED,
∴∠ADB=∠AEC,………(2分),
在△ABD和△ACE中,BD=CE,∠ADB=∠AEC,AD=AE
∴△ABD≌△ACE(SAS),………(6分),
∴AB=AC.
………(8分),
21、(8分)(1)证明:∵∠ACB=90°,CF⊥AE,∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.又∵∠DBC=∠ECA=90°,且BC=CA,
∴△DBC≌△ECA(AAS).∴AE=CD;………(4分)
(2)解:由(1)得△CDB≌△AEC,
∴BD=EC=BC=AC,且AC=12.∴BD=6.………(8分)
22、(8分)解∵AD⊥BC,∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°—90°—70°=20°;
∵∠BAC=60°,AE是∠BAC的角平分线,
∠EAC=∠BAE
=30°,
∴∠EAD=∠EAC-∠CAD=30°—20°=10°,………(5分)
∠ABC=180°—∠BAC—∠C=
50°,
∵BF是∠ABC的角平分线,∴∠ABO=25°,
∴∠BOA=180°—∠BAO—∠ABO=180°—30°—25°=125°.………(9分)
故∠DAE,∠BOA的度数分别是10°,125°.………(10分)
23【答案】【解析】EA1=FC.理由如下:………(2分)
∵AB=BC,∴∠A=∠C,
∵△ABC≌△A1BC1………(4分)
∴∠A=∠A1=∠C=∠C1
∴AB=A1B=BC=BC1
∠ABC=∠A1B
C1,
∴∠ABC﹣∠A1B
C=∠A1B
C1﹣∠A1B
C
∴∠ABE=∠C1BF………………………………………………(6分)
在△ABE与△C1BF中,
∴△ABE≌△C1BF,…………………………………………………(8分)
∴BE=BF;…………………………………………………(10分)
∴A1B﹣BE=BC﹣BF
∴EA1=FC………(12分)
(12分)详解:(1)∵∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,∴∠BAD=∠EAC.…………………………………………………(2分)
在△BAD和△CAE中,
∵,∴△BAD≌△CAE(SAS);…………………………(6分)
(2)∵△BAD≌△CAE,∴∠DBA=∠C.…………………………(8分)
∵AB=AC,∴∠C=∠ABC.…………………………(10分)
∵DF∥BC,∴∠DFB=∠ABC=∠C=∠DBA,即∠DFB=∠DBF,∴DF=CE.………(12分)
25.(12分)解:(1)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴DF=DM,
在Rt△AFD和Rt△AMD中,,∴Rt△AFD≌Rt△AMD(HL);………(4分)
(2)解:①当0<t<4时,点G在线段CM上,点E在线段AF上.
EF=10-2t,MG=4-t
∴10-2t=4-t,
∴t=6(不合题意,舍去);………………………………………………………………(6分)
②当4≤t<5时,点G在线段AM上,点E在线段AF上.
EF=10-2t,MG=t-4,
∴10-2t=t-4,
∴t=,
综上:当t=时,△DFE与△DMG全等;……………………………………………(8分)
(3)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴DF=DM,
∵S△AED=AE?DF,S△DGC=CG?DM,
∴,………(10分)
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴AE=2tcm,CG=tcm,
∴=2,
即,
∴在运动过程中,不管取何值,都有S△AED=2S△DGC.………………………(12分)
本题考查了全等三角形的判定和性质、角平分线的性质、三角形的面积公式以及动点问题,解题的难点在于第二问中求运动的时间,此题容易漏解和错解.
八年级数学科试卷
总分:150分
考试时间:120分钟
一、精心选一选,选择题:(每题只有一个正确答案,每小题4分,共40分)
1.日常生活中,我们会看到很多标志,在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A.
B.
C.
D.
2.以下列各组线段为边,能组成三角形的是(
)
A.2cm,3cm,5cm
B.5cm,6cm,10cm
C.1cm,1cm,3cm
D.3cm,4cm,9cm
3.下面四个图形中,线段BE是△ABC的高的图是(
)
A.
B.
C.
D.
4.已知△ABC≌△DEF,且AB=4,BC=5,AC=6,则DE的长为(
)
A.4
B.5
C.6
D.不能确定
5.如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的(
)
A.AB=CD
B.EC=BF
C.∠A=∠D
D.AB=BC
6.等腰三角形的两边长分别为4cm和8cm,则它的周长为(
)
A.16cm
B.17cm
C.20cm
D.16cm或20cm
7.能把一个三角形分成两个面积相等的三角形是三角形的(
)
A.中线
B.高线
C.角平分线
D.以上都不对
8.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
9.如图,△ABC中,∠C=75°,若沿图中虚线截去∠C,则∠1+∠2=(
)
A.360°
B.180°
C.255°
D.145°
10.如图:BO、CO是∠ABC,∠ACB的两条角平分线,∠A=100°,则∠BOC的度数为(
)
A.80°
B.90°
C.120°
D.140°
二、细心填一填:本大题共6小题,每小题4分,共24分.
11.如图,,,与关于直线l对称,则∠B=
.
11题图
13题图
14题图
12.若正n边形的一个外角为45°,则n=__________.
13.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5.则△BEC的周长是____.
14.如图所示,某同学将一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻
璃,那么最省事的办法是带第__________块去.(填序号)
15.如图所示,在△ABC中,∠BAC=130°,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F,则∠MAN为________.
15题图
16.如图,在中,平分交于点,点分别是和上的动点,当,时,的最小值等于__________.
16题图
三、耐心做一做(本大题共9小题,共86分)
17、(8分)如图6,∠1=∠2,∠
C=∠D,求证:AC=AD.
18、(8分)如图7,已知在中,,为边的中点,
过点作,垂足分别为.
求证:DE=DF
19、(8分)如图,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3).
(1)在图中作出△ABC关于轴的对称图形△A1B1C1.
(2)写出点A1、B1、C1的坐标.
(8分)如图8,D、E在BC上,且BD=CE,AD=AE,
求证:AB=AC.
图8
21.(8分)如图9,△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.?
求证:(1)AE=CD;
图9
(2)若AC=12,求BD的长
22、(10分)如图10所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
图10
(12分)如图11所示在△ABC中,AB=BC,△ABC≌△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想线段EA1与FC有怎样的数量关系?
并证明你的结论.
图11
24.(本题12分)如图,在△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE,点E在BC上.过点D作DF∥BC,连接DB.
求证:(1)△ABD≌△ACE;
DF=CE.
(本题12分)如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,
动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
(1)求证:AF=AM;
(2)当t取何值时,△DFE与△DMG全等;
(3)求证:在运动过程中,不管t取何值,都有
2020-2021学年上学期八年级数学期中联考(答案)
一、选择题(每小题4分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
D
A
A
C
A
B
C
D
二、填空题(每小题4分,共24分)
11、
12、
8
13、
13
14、③
15、
16、3
三、解答题(共86分)
17、证明:∵∠1=∠2,
∴∠ABC=∠ABD,在△ABD和△ABC中,…………(2分),
∵∠ABC=∠ABD
∠
C=∠D
AB=AB
∴△ABD≌△ABC(AAS),…………(6分)
∴AD=AC.
…………(8分)
证明:连接AD,∵AB=AC,D为BC的中点,
∴BD=DC,在△ABD和△ACD中,
AB=AC,BD=DC,AD=AD
∴△ABD≌△ACD(SSS)…………(3分),
∴∠BAD=∠CAD
,…………(4分)
∵…………(6分)
∴DE=DF.
…………(8分)
法2:也可以先证明△ABD≌△ACD(SSS)…(3分)再证明△ADE≌△ADF(AAS)(3分)
法3:∵AB=AC,
∴∠B=∠C,D为BC的中点,
∴BD=DC
∠BED=∠CFD…(3分),
在△BDE和△CDF中
∠B=∠C
∠BED=∠CFD
BD=DC
∴△BDE≌△CDF(AAS)(6分)
∴DE=DF.
…………(8分)
19、(1)作图
(略)…(4分),(2)A1(1,5)B1(1,0)
C1(4,3)…(4分),
20、(8分)证明:∵∠ADE=∠AED,
∴∠ADB=∠AEC,………(2分),
在△ABD和△ACE中,BD=CE,∠ADB=∠AEC,AD=AE
∴△ABD≌△ACE(SAS),………(6分),
∴AB=AC.
………(8分),
21、(8分)(1)证明:∵∠ACB=90°,CF⊥AE,∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.又∵∠DBC=∠ECA=90°,且BC=CA,
∴△DBC≌△ECA(AAS).∴AE=CD;………(4分)
(2)解:由(1)得△CDB≌△AEC,
∴BD=EC=BC=AC,且AC=12.∴BD=6.………(8分)
22、(8分)解∵AD⊥BC,∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°—90°—70°=20°;
∵∠BAC=60°,AE是∠BAC的角平分线,
∠EAC=∠BAE
=30°,
∴∠EAD=∠EAC-∠CAD=30°—20°=10°,………(5分)
∠ABC=180°—∠BAC—∠C=
50°,
∵BF是∠ABC的角平分线,∴∠ABO=25°,
∴∠BOA=180°—∠BAO—∠ABO=180°—30°—25°=125°.………(9分)
故∠DAE,∠BOA的度数分别是10°,125°.………(10分)
23【答案】【解析】EA1=FC.理由如下:………(2分)
∵AB=BC,∴∠A=∠C,
∵△ABC≌△A1BC1………(4分)
∴∠A=∠A1=∠C=∠C1
∴AB=A1B=BC=BC1
∠ABC=∠A1B
C1,
∴∠ABC﹣∠A1B
C=∠A1B
C1﹣∠A1B
C
∴∠ABE=∠C1BF………………………………………………(6分)
在△ABE与△C1BF中,
∴△ABE≌△C1BF,…………………………………………………(8分)
∴BE=BF;…………………………………………………(10分)
∴A1B﹣BE=BC﹣BF
∴EA1=FC………(12分)
(12分)详解:(1)∵∠BAC=∠DAE,
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,∴∠BAD=∠EAC.…………………………………………………(2分)
在△BAD和△CAE中,
∵,∴△BAD≌△CAE(SAS);…………………………(6分)
(2)∵△BAD≌△CAE,∴∠DBA=∠C.…………………………(8分)
∵AB=AC,∴∠C=∠ABC.…………………………(10分)
∵DF∥BC,∴∠DFB=∠ABC=∠C=∠DBA,即∠DFB=∠DBF,∴DF=CE.………(12分)
25.(12分)解:(1)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴DF=DM,
在Rt△AFD和Rt△AMD中,,∴Rt△AFD≌Rt△AMD(HL);………(4分)
(2)解:①当0<t<4时,点G在线段CM上,点E在线段AF上.
EF=10-2t,MG=4-t
∴10-2t=4-t,
∴t=6(不合题意,舍去);………………………………………………………………(6分)
②当4≤t<5时,点G在线段AM上,点E在线段AF上.
EF=10-2t,MG=t-4,
∴10-2t=t-4,
∴t=,
综上:当t=时,△DFE与△DMG全等;……………………………………………(8分)
(3)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴DF=DM,
∵S△AED=AE?DF,S△DGC=CG?DM,
∴,………(10分)
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴AE=2tcm,CG=tcm,
∴=2,
即,
∴在运动过程中,不管取何值,都有S△AED=2S△DGC.………………………(12分)
本题考查了全等三角形的判定和性质、角平分线的性质、三角形的面积公式以及动点问题,解题的难点在于第二问中求运动的时间,此题容易漏解和错解.
同课章节目录
