人教版八年级上册第十四章整式的乘除及几何表示(Word版 含答案)
文档属性
| 名称 | 人教版八年级上册第十四章整式的乘除及几何表示(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 66.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 13:18:30 | ||
图片预览

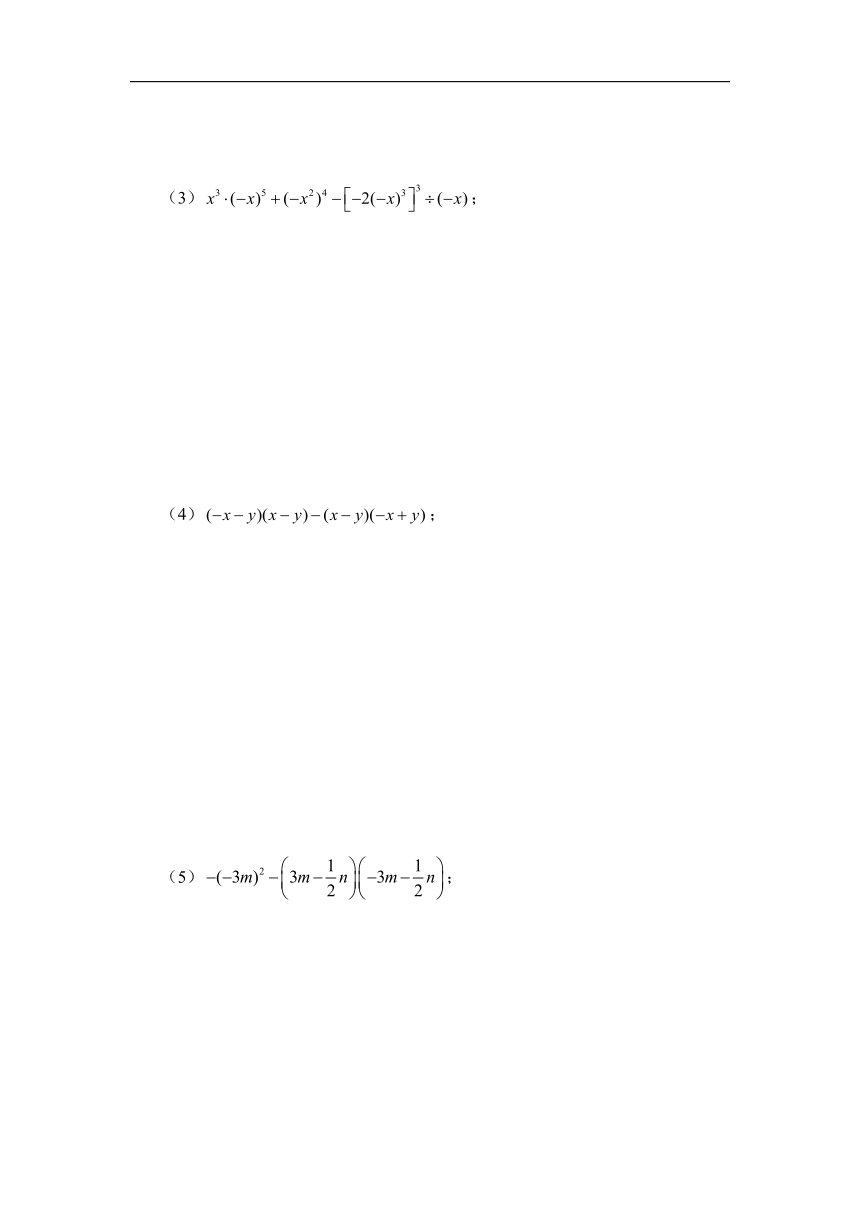

文档简介
整式的乘除及几何表示(习题)
例题示范
例1:计算:.
【思路分析】
①观察结构,分部分,这道题目可以分为_______部分.
第一部分是_________________的结构,依照法则,进行运算;
第二部分是多个单项式的乘积的结构;
第三部分是_________________的结构.
②有序操作依法则.
③每步推进一点点.
【过程示范】
巩固练习
计算下列各式:
(1);
(2);
(3);
(4);
(5);
(6).
计算下列各式:
(1);
(2).
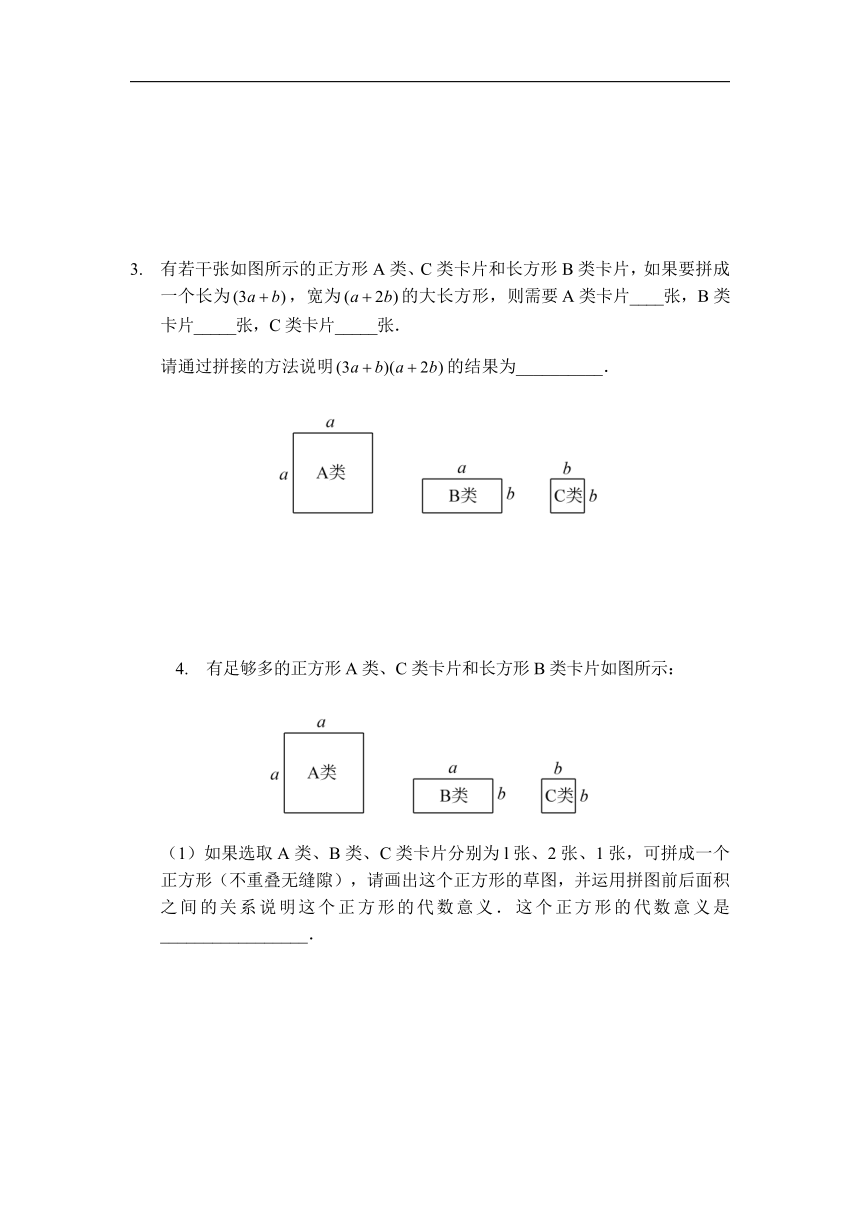
有若干张如图所示的正方形A类、C类卡片和长方形B类卡片,如果要拼成一个长为,宽为的大长方形,则需要A类卡片____张,B类卡片_____张,C类卡片_____张.
请通过拼接的方法说明的结果为__________.
有足够多的正方形A类、C类卡片和长方形B类卡片如图所示:
(1)如果选取A类、B类、C类卡片分别为l张、2张、1张,可拼成一个正方形(不重叠无缝隙),请画出这个正方形的草图,并运用拼图前后面积之间的关系说明这个正方形的代数意义.这个正方形的代数意义是_________________.
(2)小明想用类似方法解释多项式乘法,那么需用A类卡片___张,B类卡片______张,C类卡片______张.
请你用几何图形直观地解释.
请画出相应的几何图形,并根据几何图形直接写出的计算结果.
思考小结
通过本讲的学习我们知道整式的乘除可以通过图形面积的不同表达形式进行计算.小明尝试用这种方法解决:(a-b)(a-2b)时遇到了问题,经过思考后,他画出了如下图形,利用“面积”的不同表达形式可以得到:(a-b)(a-2b)=_____________;
根据小明的思路,请你通过“面积”的不同表达形式计算:
(2a-b)(a-2b)=_____________________________.
【参考答案】
例题示范
例1:【思路分析】
3
积的乘方
平方差公式
巩固练习
(1)
(2)
(3)
(4)
(5)
(6)
(1)
(2)
3
7
2
(1);
(2)4
8
3
图略
图略,
思考小结
例题示范
例1:计算:.
【思路分析】
①观察结构,分部分,这道题目可以分为_______部分.
第一部分是_________________的结构,依照法则,进行运算;
第二部分是多个单项式的乘积的结构;
第三部分是_________________的结构.
②有序操作依法则.
③每步推进一点点.
【过程示范】
巩固练习
计算下列各式:
(1);
(2);
(3);
(4);
(5);
(6).
计算下列各式:
(1);
(2).
有若干张如图所示的正方形A类、C类卡片和长方形B类卡片,如果要拼成一个长为,宽为的大长方形,则需要A类卡片____张,B类卡片_____张,C类卡片_____张.
请通过拼接的方法说明的结果为__________.
有足够多的正方形A类、C类卡片和长方形B类卡片如图所示:
(1)如果选取A类、B类、C类卡片分别为l张、2张、1张,可拼成一个正方形(不重叠无缝隙),请画出这个正方形的草图,并运用拼图前后面积之间的关系说明这个正方形的代数意义.这个正方形的代数意义是_________________.
(2)小明想用类似方法解释多项式乘法,那么需用A类卡片___张,B类卡片______张,C类卡片______张.
请你用几何图形直观地解释.
请画出相应的几何图形,并根据几何图形直接写出的计算结果.
思考小结
通过本讲的学习我们知道整式的乘除可以通过图形面积的不同表达形式进行计算.小明尝试用这种方法解决:(a-b)(a-2b)时遇到了问题,经过思考后,他画出了如下图形,利用“面积”的不同表达形式可以得到:(a-b)(a-2b)=_____________;
根据小明的思路,请你通过“面积”的不同表达形式计算:
(2a-b)(a-2b)=_____________________________.
【参考答案】
例题示范
例1:【思路分析】
3
积的乘方
平方差公式
巩固练习
(1)
(2)
(3)
(4)
(5)
(6)
(1)
(2)
3
7
2
(1);
(2)4
8
3
图略
图略,
思考小结
