人教版数学七年级下册 第9章不等式与不等式组课时2 课件(24张)
文档属性
| 名称 | 人教版数学七年级下册 第9章不等式与不等式组课时2 课件(24张) |  | |
| 格式 | zip | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 12:56:00 | ||
图片预览








文档简介
(共24张PPT)
9
小结
课时2
不等式与不等式组
人教版-数学-七年级-下册
知识梳理-重点解析-深化练习
知识梳理
把几个具有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组
一元一次不等式组
定义
不等式组的解集的确定
数轴法
口诀法:同大取大,同小取小,大大小小无处找,大小小大中间找
几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集
不等式组的解集
(1)分别求出不等式组中各个不等式的解集;
(2)求出各个不等式的解集的公共部分
解不等式组的步骤
知识梳理
分析已知量、未知量及它们之间的关系,找出题目中的不等关系.
审
设出合适的未知数.
设
根据题中的不等关系列出不等式组.
列
解不等式组,求出其解集.
解
检验所求出的不等式组的解集是否符合题意.
验
写出答案.
答
用一元一次不等式组解决实际问题的步骤
知识梳理
7.一元一次不等式组
类似于方程组,把几个_________________的一元一次不等式合起来,就组成一个一元一次不等式组.
一元一次不等式组必须同时满足三个条件:
①每个不等式都是一元一次不等式;
②含有同一个未知数;
③不等式的个数不少于2.
含有相同未知数
知识梳理
8.一元一次不等式组的解集
一般地,几个不等式的_________________,叫做由它们所组成的不等式组的解集.
“公共部分”是指同时满足不等式组中每一个不等式的解集的部分.如果组成不等式组的各个不等式的解集没有公共部分,则这个不等式组无解.
解集的公共部分
知识梳理
确定一元一次不等式组的解集的两种方法
(1)数轴法:即先把不等式组中每个不等式的解集在数轴上表示出来,找出它们的公共部分,就得到不等式组的解集,若无公共部分,则不等式组无解;
(2)口诀法:同大取大,同小取小,大大小小无处找,大小小大中间找.
知识梳理
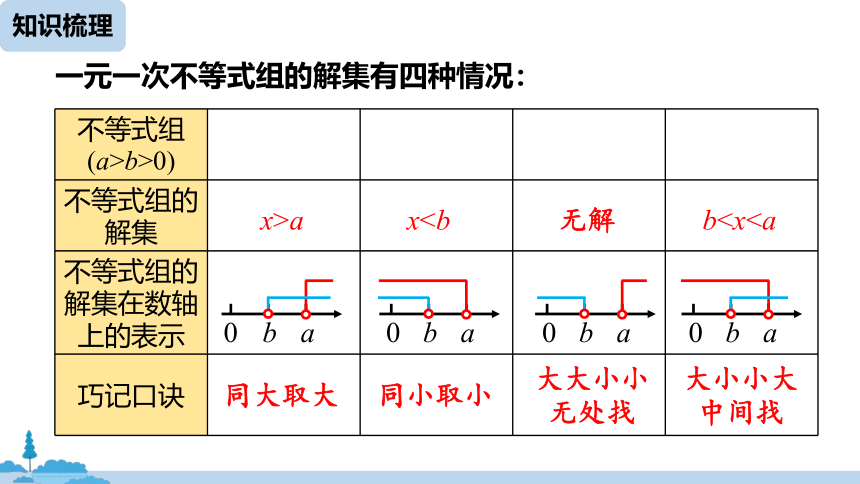
一元一次不等式组的解集有四种情况:
不等式组
(a>b>0)
不等式组的解集
不等式组的解集在数轴上的表示
巧记口诀
x>a
x无解
b同大取大
同小取小
大大小小无处找
大小小大中间找
b
0
a
b
0
a
b
0
a
b
0
a
知识梳理
9.列一元一次不等式组解决实际问题的步骤:
(1)审:分析已知量、未知量及它们之间的关系,找出题目中的不等关系;
(2)设:设出合适的未知数;
(3)列:根据题目中的不等关系,列出一元一次不等式组;
(4)解:解不等式组(可以借助数轴也可以用“口诀”);
(5)验:检验所求出的不等式组的解集是否符合题意及实际意义;
(6)答:写出答案.
重点解析
重难点1:一元一次不等式组的定义
下列选项中是一元一次不等式组的是(
)
A.
B.
C.
D.
三个未知数
两个未知数
最高次数为2
D
重点解析
重难点2:解一元一次不等式组
1.解不等式组:
解:解不等式①,得
x≥-2.
解不等式②,得
x<1.
把不等式①和②的解集在数轴上表示出来,如下图所示.
2
0
-3
-2
-1
1
3
由图可得不等式组的解集为
-2≤x<1.
重点解析
2.已知不等式组
有解,则
a
的取值范围为(
)
A.
a>-2
B.
a≥-2
C.
a<2
D.
a≥2
C
x≥a
x<2
3.若关于
x
的不等式组
的整数解共有
3
个,则
m
的取值范围是(
)
A.5B.5C.5≤m≤6
D.6xx≥3
不等式组的解集
3≤x3,4,5
B
重点解析
重难点3:用一元一次不等式组解决实际问题
1.一堆玩具分给若干个小朋友,若每人分
3
件,则剩余
4件;若前面每人分
4
件,则最后一人得到的玩具不足
3件,求小朋友的人数与玩具数.
x
玩具数:3x+4
0≤3x+4-4(x-1)<3
重点解析
解:设小朋友总共有
x
人,
根据题意,得
解得
5因为
x
是整数,所以
x=6,7,8.
答:小朋友有
6
人,玩具有
22件;或小朋友有
7
人,玩具有
25
件;或小朋友有
8
人,玩具有
28
件.
2.某服装厂现有
A
种布料
70
m,B
种布料
52
m,现计划用这两种布料生产
M,N
两种型号的时装共
80
套,已知做一套
M
型号的时装需用
A
种布料
0.6
m,B
种布料0.9
m,可获得利润
45
元;做一套
N
型号的时装需用
A种布料
1.1
m,B
种布料
0.4
m,可获得利润
50
元.
该服装厂在生产这批时装时,当生产
N
型号的时装多少套时,所获得的利润最大?最大利润为多少?
重点解析
解:设生产
N
型号的时装
x
套,
由题意得
解得
40≤x≤44.
x
80-x
A:0.6(80-x)
B:0.9(80-x)
A:1.1x
B:0.4x
由题意得获得的利润为
y=50x+45(80-x),
当
x=40时,y=3800;
当
x=41时,y=3805;
当
x=42时,y=3810;
当
x=43时,y=3815;
当
x=44时,y=3820.
故当生产
N
型号的时装
44
套时,所获得的利润最大,最大利润为
3820
元.
重点解析
深化练习
1.下列不等式组中是一元一次不等式组的个数是(
)
①
②
③
④
A.
1
个
B.
2
个
C.
3
个
D.
4
个
两个未知数
最高次为2
B
深化练习
2.不等式组
的所有整数解的和是
.
9
x>1
x≤4
2+3+4=9
解集:1深化练习
3.若关于
x
的不等式组
仅有四个整数解,则
a
的取值范围是(
)
A.1≤a≤2
B.1≤a<2
C.1<a<2
D.a<2
x>a-1
x≤4
解集:a-1整数解:1,2,3,4
0≤a-1<1
1≤a<2
B
深化练习
4.
3
个小组计划在
10
天内生产
500
件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产
1
件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
3×10x<500
3×10(x+1)>500
解:设每个小组原先每天生产
x
件产品,
根据题意,得
解不等式组,得
.
根据题意,x
的值应是整数,所以
x=16.
答:每个小组原先每天生产
16
件产品.
x
5.某中学组织部分班级开展研学旅行活动.在参加此次活动的师生中,若每名老师带
17
个学生,还剩
12
个学生没人带;若每名老师带
18
个学生,就有一名老师少带
4
个学生.为了安全,每辆客车上至少要有
2
名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
解:(1)设老师有
x
人,学生有
y
人.
依题意得
解得
答:此次参加研学旅行活动的老师有
16
人,学生有
284
人.
深化练习
(2)现有甲、乙两种大客车,它们的载客量和租金如下表所示:
?
甲种客车
乙种客车
载客量/(人/辆)
30
42
租金/(元/辆)
300
400
学校计划此次研学旅行活动的租车总费用不超过
3100
元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
深化练习
(2)
∵每辆客车上至少要有
2
名老师,
∴汽车总数不能超过
8
辆;
又要保证
300
名师生有车坐,汽车总数不能小于
(取整为8)辆,
综合起来可知汽车总数为
8
辆.
深化练习
设乙种客车租
a
辆,则甲种客车租(8-a)辆.
∵
租车总费用不超过
3100
元,
∴
400a+300(8-a)≤3
100,
解得
a≤7.
为使
300
名师生都有车坐,有
42a+30(8-a)≥300,
解得
a≥5.
∴
5≤a≤7(a
为整数).
深化练习
∴
共有
3
种租车方案:
方案一:租用甲种客车
3
辆、乙种客车
5
辆,租车费用为
2900
元;
方案二:租用甲种客车
2
辆、乙种客车
6
辆,租车费用为
3000
元;
方案三:租用甲种客车
1
辆、乙种客车
7
辆,租车费用为
3100
元;
∴最节省费用的租车方案是:租用甲种客车
3
辆、乙种客车
5
辆.
深化练习
9
小结
课时2
不等式与不等式组
人教版-数学-七年级-下册
知识梳理-重点解析-深化练习
知识梳理
把几个具有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组
一元一次不等式组
定义
不等式组的解集的确定
数轴法
口诀法:同大取大,同小取小,大大小小无处找,大小小大中间找
几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集
不等式组的解集
(1)分别求出不等式组中各个不等式的解集;
(2)求出各个不等式的解集的公共部分
解不等式组的步骤
知识梳理
分析已知量、未知量及它们之间的关系,找出题目中的不等关系.
审
设出合适的未知数.
设
根据题中的不等关系列出不等式组.
列
解不等式组,求出其解集.
解
检验所求出的不等式组的解集是否符合题意.
验
写出答案.
答
用一元一次不等式组解决实际问题的步骤
知识梳理
7.一元一次不等式组
类似于方程组,把几个_________________的一元一次不等式合起来,就组成一个一元一次不等式组.
一元一次不等式组必须同时满足三个条件:
①每个不等式都是一元一次不等式;
②含有同一个未知数;
③不等式的个数不少于2.
含有相同未知数
知识梳理
8.一元一次不等式组的解集
一般地,几个不等式的_________________,叫做由它们所组成的不等式组的解集.
“公共部分”是指同时满足不等式组中每一个不等式的解集的部分.如果组成不等式组的各个不等式的解集没有公共部分,则这个不等式组无解.
解集的公共部分
知识梳理
确定一元一次不等式组的解集的两种方法
(1)数轴法:即先把不等式组中每个不等式的解集在数轴上表示出来,找出它们的公共部分,就得到不等式组的解集,若无公共部分,则不等式组无解;
(2)口诀法:同大取大,同小取小,大大小小无处找,大小小大中间找.
知识梳理
一元一次不等式组的解集有四种情况:
不等式组
(a>b>0)
不等式组的解集
不等式组的解集在数轴上的表示
巧记口诀
x>a
x
b
同小取小
大大小小无处找
大小小大中间找
b
0
a
b
0
a
b
0
a
b
0
a
知识梳理
9.列一元一次不等式组解决实际问题的步骤:
(1)审:分析已知量、未知量及它们之间的关系,找出题目中的不等关系;
(2)设:设出合适的未知数;
(3)列:根据题目中的不等关系,列出一元一次不等式组;
(4)解:解不等式组(可以借助数轴也可以用“口诀”);
(5)验:检验所求出的不等式组的解集是否符合题意及实际意义;
(6)答:写出答案.
重点解析
重难点1:一元一次不等式组的定义
下列选项中是一元一次不等式组的是(
)
A.
B.
C.
D.
三个未知数
两个未知数
最高次数为2
D
重点解析
重难点2:解一元一次不等式组
1.解不等式组:
解:解不等式①,得
x≥-2.
解不等式②,得
x<1.
把不等式①和②的解集在数轴上表示出来,如下图所示.
2
0
-3
-2
-1
1
3
由图可得不等式组的解集为
-2≤x<1.
重点解析
2.已知不等式组
有解,则
a
的取值范围为(
)
A.
a>-2
B.
a≥-2
C.
a<2
D.
a≥2
C
x≥a
x<2
3.若关于
x
的不等式组
的整数解共有
3
个,则
m
的取值范围是(
)
A.5
D.6
不等式组的解集
3≤x
B
重点解析
重难点3:用一元一次不等式组解决实际问题
1.一堆玩具分给若干个小朋友,若每人分
3
件,则剩余
4件;若前面每人分
4
件,则最后一人得到的玩具不足
3件,求小朋友的人数与玩具数.
x
玩具数:3x+4
0≤3x+4-4(x-1)<3
重点解析
解:设小朋友总共有
x
人,
根据题意,得
解得
5
x
是整数,所以
x=6,7,8.
答:小朋友有
6
人,玩具有
22件;或小朋友有
7
人,玩具有
25
件;或小朋友有
8
人,玩具有
28
件.
2.某服装厂现有
A
种布料
70
m,B
种布料
52
m,现计划用这两种布料生产
M,N
两种型号的时装共
80
套,已知做一套
M
型号的时装需用
A
种布料
0.6
m,B
种布料0.9
m,可获得利润
45
元;做一套
N
型号的时装需用
A种布料
1.1
m,B
种布料
0.4
m,可获得利润
50
元.
该服装厂在生产这批时装时,当生产
N
型号的时装多少套时,所获得的利润最大?最大利润为多少?
重点解析
解:设生产
N
型号的时装
x
套,
由题意得
解得
40≤x≤44.
x
80-x
A:0.6(80-x)
B:0.9(80-x)
A:1.1x
B:0.4x
由题意得获得的利润为
y=50x+45(80-x),
当
x=40时,y=3800;
当
x=41时,y=3805;
当
x=42时,y=3810;
当
x=43时,y=3815;
当
x=44时,y=3820.
故当生产
N
型号的时装
44
套时,所获得的利润最大,最大利润为
3820
元.
重点解析
深化练习
1.下列不等式组中是一元一次不等式组的个数是(
)
①
②
③
④
A.
1
个
B.
2
个
C.
3
个
D.
4
个
两个未知数
最高次为2
B
深化练习
2.不等式组
的所有整数解的和是
.
9
x>1
x≤4
2+3+4=9
解集:1
3.若关于
x
的不等式组
仅有四个整数解,则
a
的取值范围是(
)
A.1≤a≤2
B.1≤a<2
C.1<a<2
D.a<2
x>a-1
x≤4
解集:a-1
0≤a-1<1
1≤a<2
B
深化练习
4.
3
个小组计划在
10
天内生产
500
件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产
1
件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
3×10x<500
3×10(x+1)>500
解:设每个小组原先每天生产
x
件产品,
根据题意,得
解不等式组,得
.
根据题意,x
的值应是整数,所以
x=16.
答:每个小组原先每天生产
16
件产品.
x
5.某中学组织部分班级开展研学旅行活动.在参加此次活动的师生中,若每名老师带
17
个学生,还剩
12
个学生没人带;若每名老师带
18
个学生,就有一名老师少带
4
个学生.为了安全,每辆客车上至少要有
2
名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
解:(1)设老师有
x
人,学生有
y
人.
依题意得
解得
答:此次参加研学旅行活动的老师有
16
人,学生有
284
人.
深化练习
(2)现有甲、乙两种大客车,它们的载客量和租金如下表所示:
?
甲种客车
乙种客车
载客量/(人/辆)
30
42
租金/(元/辆)
300
400
学校计划此次研学旅行活动的租车总费用不超过
3100
元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
深化练习
(2)
∵每辆客车上至少要有
2
名老师,
∴汽车总数不能超过
8
辆;
又要保证
300
名师生有车坐,汽车总数不能小于
(取整为8)辆,
综合起来可知汽车总数为
8
辆.
深化练习
设乙种客车租
a
辆,则甲种客车租(8-a)辆.
∵
租车总费用不超过
3100
元,
∴
400a+300(8-a)≤3
100,
解得
a≤7.
为使
300
名师生都有车坐,有
42a+30(8-a)≥300,
解得
a≥5.
∴
5≤a≤7(a
为整数).
深化练习
∴
共有
3
种租车方案:
方案一:租用甲种客车
3
辆、乙种客车
5
辆,租车费用为
2900
元;
方案二:租用甲种客车
2
辆、乙种客车
6
辆,租车费用为
3000
元;
方案三:租用甲种客车
1
辆、乙种客车
7
辆,租车费用为
3100
元;
∴最节省费用的租车方案是:租用甲种客车
3
辆、乙种客车
5
辆.
深化练习
