4.3.3 余角和补角 课件(共26张PPT)
文档属性
| 名称 | 4.3.3 余角和补角 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 00:00:00 | ||
图片预览


文档简介
4.3.3 余角和补角
人教版 七上
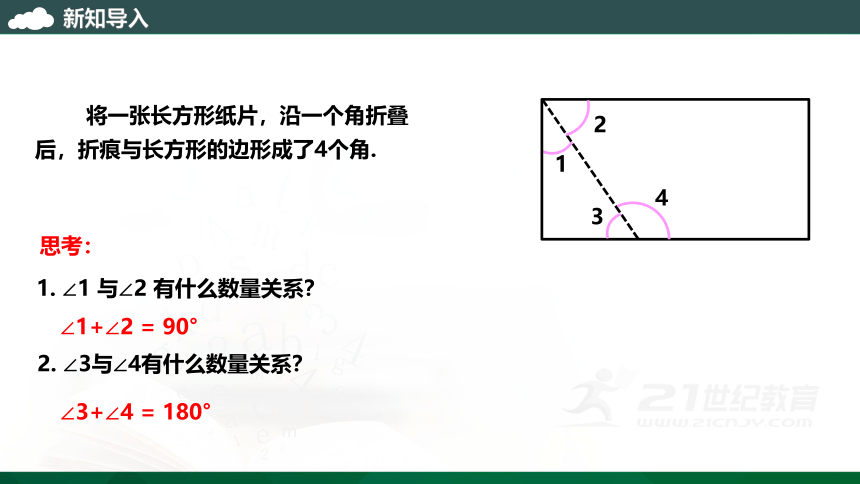
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
∠1+∠2 = 90°
思考:
1. ∠1 与∠2 有什么数量关系?
2. ∠3与∠4有什么数量关系?
∠3+∠4 = 180°
新知导入
1
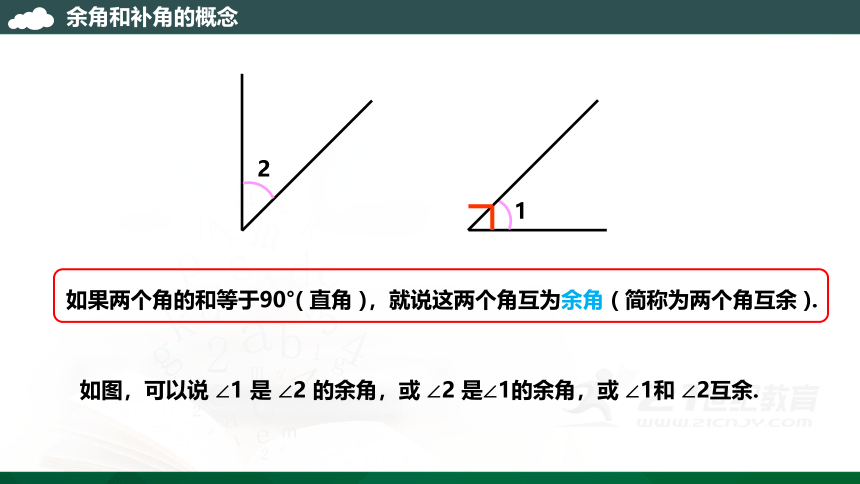
如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如图,可以说 ∠1 是 ∠2 的余角,或 ∠2 是∠1的余角,或 ∠1和 ∠2互余.
2
余角和补角的概念
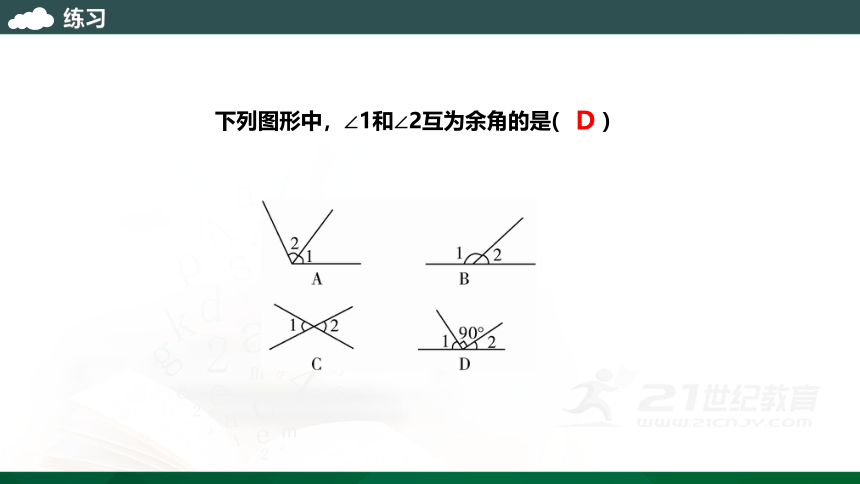
下列图形中,∠1和∠2互为余角的是( )
D
练习
思考:
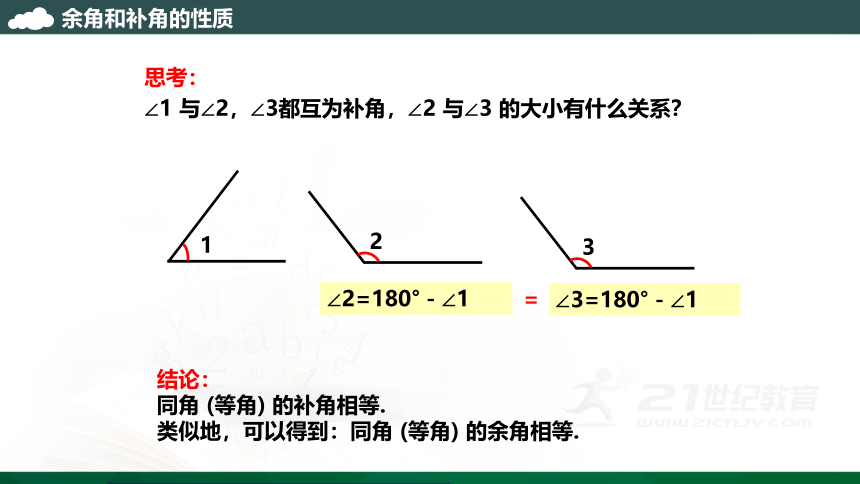
∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
1
2
结论:
同角 (等角) 的补角相等.
类似地,可以得到:同角 (等角) 的余角相等.
3
∠2=180°-∠1
∠3=180°-∠1
=
余角和补角的性质
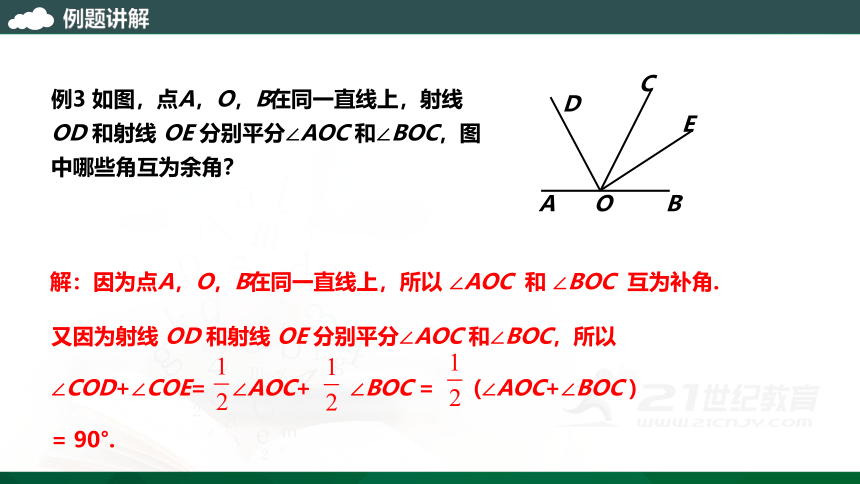
例3 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线上,所以 ∠AOC 和 ∠BOC 互为补角.
O
A
B
C
D
E
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,所以∠COD+∠COE= ∠AOC+ ∠BOC = (∠AOC+∠BOC )
= 90°.
例题讲解
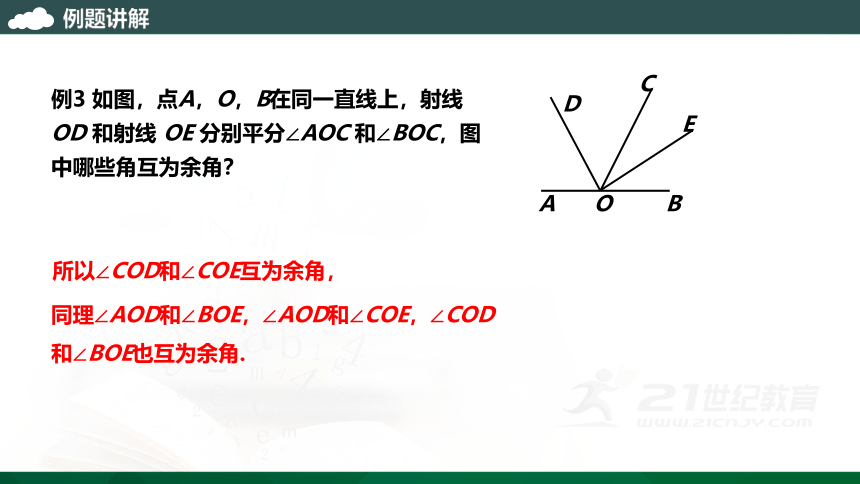
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
例题讲解
例3 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
O
A
B
C
D
E
若一个角的补角等于它的余角的 4 倍,求这个角的度数.
解:设这个角为 x°,则它的补角是 ( 180-x )°,
余角是 ( 90-x )° .
根据题意,得180-x = 4 ( 90-x ) .
解得 x = 60.
答:这个角的度数是 60 °.
变式训练
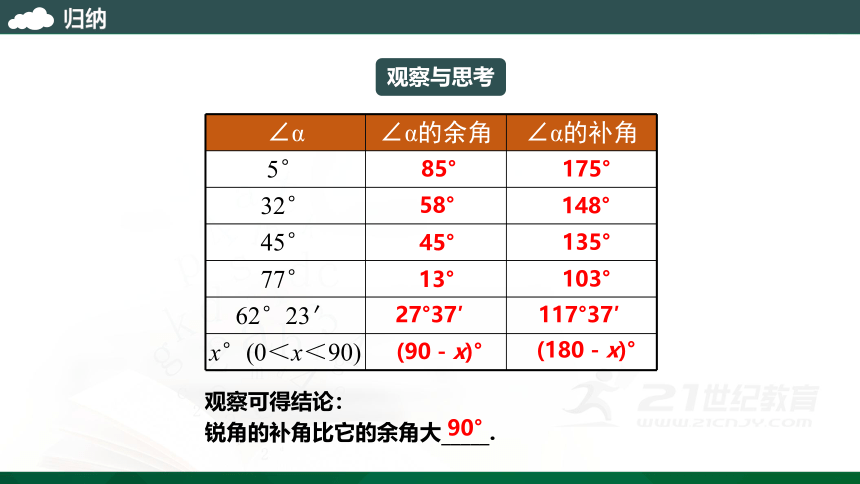
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}∠α
∠α的余角
∠α的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
观察与思考
(90-x)°
(180-x)°
观察可得结论:
锐角的补角比它的余角大_____.
90°
归纳
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
方位角
45°
如图,说出下列方位
(1) 射线 OA 表示的方向
为 .
(2) 射线 OB 表示的方向
为 ___ _ .
(3) 射线 OC 表示的方向
为 .
(4) 射线 OD 表示的方向
为 .
北
东
西
南
C
A
B
D
北偏东 40°
北偏西 65°
南偏西 45°(西南)
南偏东 20°
40°
65°
70°
O
20°
方位角
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上. 同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)
方向上又分别发现了客
轮B,货轮C和海岛D.
仿照表示灯塔方位的
方法画出表示客轮B,
货轮C和海岛D方向的
射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● A
● D
O
●
例题讲解
费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
●
●
远望一号
远望二号
变式训练
●
●
远望一号
远望二号
60°
30°
●
变式训练
要点1 余角、补角的概念与性质
1. 一般地,如果两个角的和等于 ,就说这两个角互为余角,即其中一个角是另一个角的 ;类似地,如果两个角的和等于 ,就说这两个角互为补角,即其中一个角是另一个角的 .
2. 同角(等角)的补角 ,同角(等角)的余角 .
要点1 1. 90° 余角 180° 补角 2. 相等 相等
课后练习
要点2 方位角
方位角就是表示 的角,一般以 、 方向为基准,描述物体运动的方向.记录时,通常要先写 偏或 偏,再写东或西.
要点2 方向 正北 正南 北 南
课后练习
1.已知∠A=65°,则∠A的补角等于( )
A.125° B.105° C.115° D.95°
C
课后练习
2.已知α=36°42′,则α的余角为( )
A.57°18′ B.52°18′ C.53°18′ D.36°43′
C
课后练习
3.对于互补的下列说法中:①∠A+∠B+∠C=90°,则∠A,∠B,∠C互补;②若∠1是∠2的补角,则∠2是∠1的补角;③同一个锐角的补角一定比它的余角大90°;④互补的两个角中,一定是一个钝角与一个锐角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
课后练习
4.如图,下列说法正确的个数有( )
①射线OA表示北偏东30°;
②射线OB表示北偏西30°;
③射线OD表示南偏西45°,
也叫西南方向;
④射线OC表示正南方向.
A.1个 B.2个 C.3个 D.4个
D
课后练习
5. 如图,∠AOB=160°,∠AOD与∠DOC互余,∠BOD=90°,求∠COD的度数.
解:因为∠AOB=160°,∠BOD=90°,
所以∠AOD=70°.
因为∠AOD与∠DOC互余,所以∠AOD+∠DOC=90°.
所以∠COD=90°-∠AOD=90°-70°=20°.
课后练习
6. 甲、乙两船同时从小岛A出发,甲的速度为30海里/时,向北偏东20°方向航行,乙沿南偏东70°的方向以40海里/时的速度航行,半小时后甲、乙分别到达B,C两处.
(1)以1cm表示10海里,在图中画出B,C的位置;
(2)求∠BAC的度数;
(3)量出B,C的图上距离,并换算出实际距离.
解:(1)如图,
(2)∠BAC=180°-20°-70°=90°.
(3)用刻度尺量出B,C的图上距离约为2.5cm,所以实际距离约为25海里.
课后练习
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
对应图形
性质
课堂总结
教材练习题1—3题.
布置作业
谢谢聆听
人教版 七上
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
1
2
3
4
∠1+∠2 = 90°
思考:
1. ∠1 与∠2 有什么数量关系?
2. ∠3与∠4有什么数量关系?
∠3+∠4 = 180°
新知导入
1
如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ).
如图,可以说 ∠1 是 ∠2 的余角,或 ∠2 是∠1的余角,或 ∠1和 ∠2互余.
2
余角和补角的概念
下列图形中,∠1和∠2互为余角的是( )
D
练习
思考:
∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
1
2
结论:
同角 (等角) 的补角相等.
类似地,可以得到:同角 (等角) 的余角相等.
3
∠2=180°-∠1
∠3=180°-∠1
=
余角和补角的性质
例3 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线上,所以 ∠AOC 和 ∠BOC 互为补角.
O
A
B
C
D
E
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,所以∠COD+∠COE= ∠AOC+ ∠BOC = (∠AOC+∠BOC )
= 90°.
例题讲解
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
例题讲解
例3 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
O
A
B
C
D
E
若一个角的补角等于它的余角的 4 倍,求这个角的度数.
解:设这个角为 x°,则它的补角是 ( 180-x )°,
余角是 ( 90-x )° .
根据题意,得180-x = 4 ( 90-x ) .
解得 x = 60.
答:这个角的度数是 60 °.
变式训练
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}∠α
∠α的余角
∠α的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
观察与思考
(90-x)°
(180-x)°
观察可得结论:
锐角的补角比它的余角大_____.
90°
归纳
东
西
北
南
O
正东:
正南:
正西:
正北:
西北方向:
西南方向:
东北方向:
东南方向:
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
方位角
45°
如图,说出下列方位
(1) 射线 OA 表示的方向
为 .
(2) 射线 OB 表示的方向
为 ___ _ .
(3) 射线 OC 表示的方向
为 .
(4) 射线 OD 表示的方向
为 .
北
东
西
南
C
A
B
D
北偏东 40°
北偏西 65°
南偏西 45°(西南)
南偏东 20°
40°
65°
70°
O
20°
方位角
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上. 同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)
方向上又分别发现了客
轮B,货轮C和海岛D.
仿照表示灯塔方位的
方法画出表示客轮B,
货轮C和海岛D方向的
射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● A
● D
O
●
例题讲解
费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
●
●
远望一号
远望二号
变式训练
●
●
远望一号
远望二号
60°
30°
●
变式训练
要点1 余角、补角的概念与性质
1. 一般地,如果两个角的和等于 ,就说这两个角互为余角,即其中一个角是另一个角的 ;类似地,如果两个角的和等于 ,就说这两个角互为补角,即其中一个角是另一个角的 .
2. 同角(等角)的补角 ,同角(等角)的余角 .
要点1 1. 90° 余角 180° 补角 2. 相等 相等
课后练习
要点2 方位角
方位角就是表示 的角,一般以 、 方向为基准,描述物体运动的方向.记录时,通常要先写 偏或 偏,再写东或西.
要点2 方向 正北 正南 北 南
课后练习
1.已知∠A=65°,则∠A的补角等于( )
A.125° B.105° C.115° D.95°
C
课后练习
2.已知α=36°42′,则α的余角为( )
A.57°18′ B.52°18′ C.53°18′ D.36°43′
C
课后练习
3.对于互补的下列说法中:①∠A+∠B+∠C=90°,则∠A,∠B,∠C互补;②若∠1是∠2的补角,则∠2是∠1的补角;③同一个锐角的补角一定比它的余角大90°;④互补的两个角中,一定是一个钝角与一个锐角.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
课后练习
4.如图,下列说法正确的个数有( )
①射线OA表示北偏东30°;
②射线OB表示北偏西30°;
③射线OD表示南偏西45°,
也叫西南方向;
④射线OC表示正南方向.
A.1个 B.2个 C.3个 D.4个
D
课后练习
5. 如图,∠AOB=160°,∠AOD与∠DOC互余,∠BOD=90°,求∠COD的度数.
解:因为∠AOB=160°,∠BOD=90°,
所以∠AOD=70°.
因为∠AOD与∠DOC互余,所以∠AOD+∠DOC=90°.
所以∠COD=90°-∠AOD=90°-70°=20°.
课后练习
6. 甲、乙两船同时从小岛A出发,甲的速度为30海里/时,向北偏东20°方向航行,乙沿南偏东70°的方向以40海里/时的速度航行,半小时后甲、乙分别到达B,C两处.
(1)以1cm表示10海里,在图中画出B,C的位置;
(2)求∠BAC的度数;
(3)量出B,C的图上距离,并换算出实际距离.
解:(1)如图,
(2)∠BAC=180°-20°-70°=90°.
(3)用刻度尺量出B,C的图上距离约为2.5cm,所以实际距离约为25海里.
课后练习
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
对应图形
性质
课堂总结
教材练习题1—3题.
布置作业
谢谢聆听
