4.3.1 角(共26张PPT)
图片预览






文档简介
4.3.1 角
人教版 七上
观察左边的实物,你发现这些实物能抽象出什么样的共同形象?
——角
新知导入
你能归纳出角的特点吗?用自己的话描述一下角是由什么组成的图形?
定义
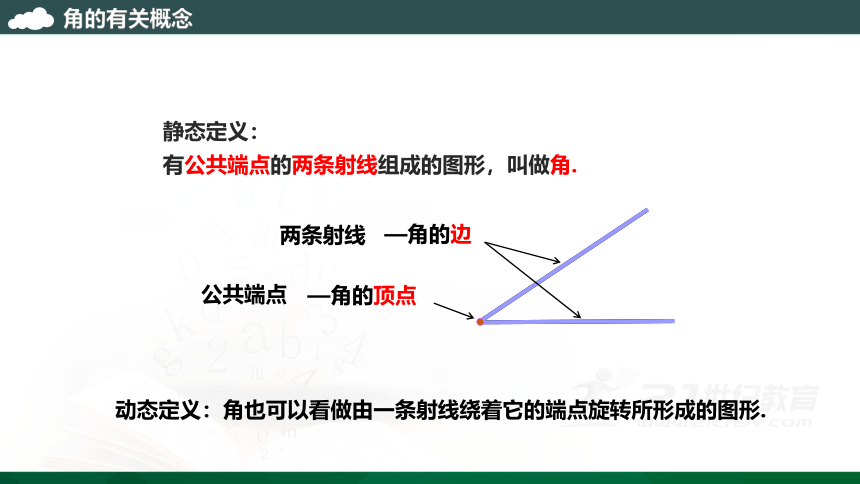
静态定义:
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的边
动态定义:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
角的有关概念
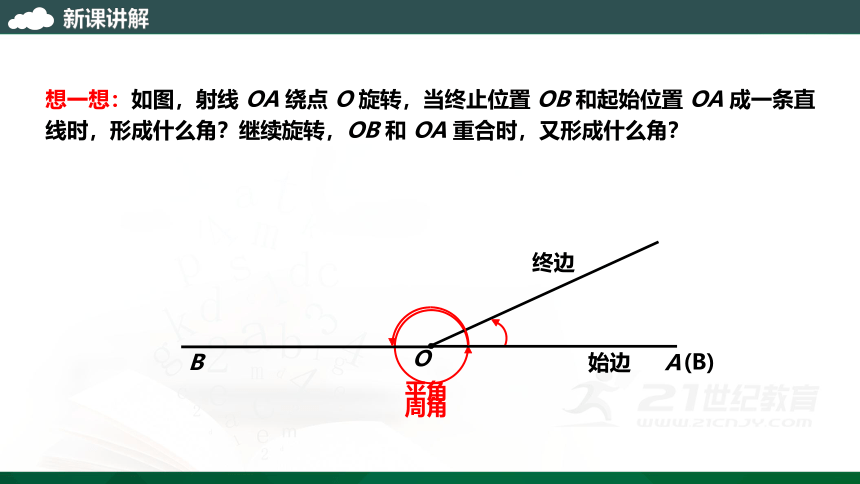
始边
终边
O
A
B
(B)
平角
周角
想一想:如图,射线 OA 绕点 O 旋转,当终止位置 OB 和起始位置 OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
新课讲解
1. 角是指( )
A. 由两条射线组成的图形 B. 由两条线段组成的图形
C. 由两条直线组成的图形 D. 有公共端点的两条射线组成的图形
D
练习
(注意
必须把顶点字母放在中间)
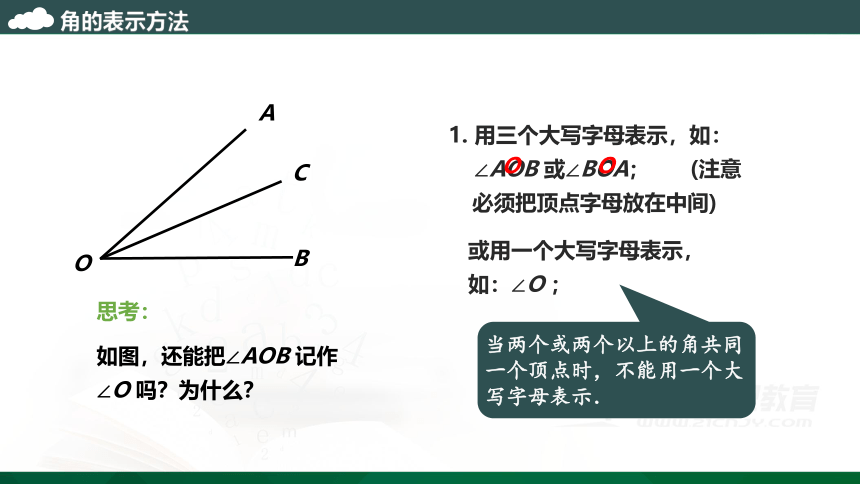
1. 用三个大写字母表示,如:
∠AOB 或∠BOA;
或用一个大写字母表示,
如:∠O ;
当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示.
A
B
O
思考:
如图,还能把∠AOB 记作∠O 吗?为什么?
C
O O
角的表示方法
2. 用一个数字表示, 如∠1;
3. 用小写希腊字母表示,如∠α.
α
1
A
B
O
C
用数字或希腊字母
表示角时,一定要在图形
中用角弧标出.
.
角的表示方法
如图所示,下列表示∠1正确的是( )
A. ∠O B. ∠AOB C. ∠AOC D. ∠OAC
C
练习
角的度量工具:量角器
怎么知道这个角的大小?
角的度量
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分,每一份就是 1 度的角,记作1°;把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
角的度量
例 度分秒的互化
(1) 57.32°= ° ′ ″;
解析:57.32?=57?+0.32×60′
=57?+19.2′
=57?19′+0.2×60″
=57?19′12″
按1°=60′,1′=60″,先把度化成分,再把分化成秒. (小数化整数)
57
19
12
新课讲解
用度、分、秒表示:78.43°.
解:∵78.43°=78°+0.43°,
0.43°=60′×0.43=25.8′,0.8′=60′×0.8=48″,
∴78.43°=78°25′48″.
新课讲解
(1)3.76°= 度 分 秒.
(2)上午10点30分时,时针与分针的夹角的度数是 .
练习
3
45
36
135°
要点1 角的概念
1. 有公共端点的 射线组成的图形叫做角,角也可以看作是一条射线绕着它的端点 而成的图形.
2. 角的表示方法:用三个 表示,顶点必须写在 ;用一个大写字母;一个数字或 字母.
要点1 1. 两条 旋转 2. 大写字母 中间 希腊
课堂练习
要点2 角的度量
1. 角的度量工具: .
2. 角的度量单位: 、 、 .
1周角= °,1平角= °,1°= ′,1′= ″.
要点2 1. 量角器 2. 度 分 秒 360 180 60 60
课堂练习
1. 一个齿轮板有36个齿,每相邻两齿中心线间的夹角都相等,这个夹角是( )
A. 36° B. 18° C.10° D. 42°
C
课堂练习
2. 已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是( )
A. ∠α=∠β B. ∠α<∠β C. ∠α=∠γ D. ∠β>∠γ
C
课堂练习
3. 下列能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
A B C D
B
课堂练习
4. 如图所示,将一个矩形沿图中的虚线折叠,请用量角器量一下其中的α,β,得∠α ∠β.(填“>”“=”或“<”)
=
课堂练习
5.用度数表示下列各角度:
(1)37°54′; (2)45°12′;
(3)31°48′; (4)4°51′.
解:(1)54′=(54÷60)°=0.9°,即37°54′=37.9°.
(2)12″=(12÷60)°=0.2°,即45°12′=45.2°.
(3)48′=(48÷60)°=0.8°,即31°48′=31.8°.
(4)51′=(51÷60)°=0.85°,即4°51′=4.85°.
课堂练习
6.计算:180°-(38°45′+72.5°).
解:180°-(38°45′+72.5°)
=180°-(38°45′+72°30′),
=180°-111°15′,
=68°45′.
课堂练习
角的定义
有公共端点的两条射线组成的图形
一条射线绕着它的端点旋转而形成的图形
角的表示方法
用三个大写字母或一个大写字母表示
用一个数字加弧线表示
用一个小写希腊字母加弧线表示
角的度量
度、分、秒
1°=60′,1′=60″
课后总结
教材练习题1—3题.
布置作业
谢谢聆听
人教版 七上
观察左边的实物,你发现这些实物能抽象出什么样的共同形象?
——角
新知导入
你能归纳出角的特点吗?用自己的话描述一下角是由什么组成的图形?
定义
静态定义:
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的边
动态定义:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
角的有关概念
始边
终边
O
A
B
(B)
平角
周角
想一想:如图,射线 OA 绕点 O 旋转,当终止位置 OB 和起始位置 OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
新课讲解
1. 角是指( )
A. 由两条射线组成的图形 B. 由两条线段组成的图形
C. 由两条直线组成的图形 D. 有公共端点的两条射线组成的图形
D
练习
(注意
必须把顶点字母放在中间)
1. 用三个大写字母表示,如:
∠AOB 或∠BOA;
或用一个大写字母表示,
如:∠O ;
当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示.
A
B
O
思考:
如图,还能把∠AOB 记作∠O 吗?为什么?
C
O O
角的表示方法
2. 用一个数字表示, 如∠1;
3. 用小写希腊字母表示,如∠α.
α
1
A
B
O
C
用数字或希腊字母
表示角时,一定要在图形
中用角弧标出.
.
角的表示方法
如图所示,下列表示∠1正确的是( )
A. ∠O B. ∠AOB C. ∠AOC D. ∠OAC
C
练习
角的度量工具:量角器
怎么知道这个角的大小?
角的度量
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分,每一份就是 1 度的角,记作1°;把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
角的度量
例 度分秒的互化
(1) 57.32°= ° ′ ″;
解析:57.32?=57?+0.32×60′
=57?+19.2′
=57?19′+0.2×60″
=57?19′12″
按1°=60′,1′=60″,先把度化成分,再把分化成秒. (小数化整数)
57
19
12
新课讲解
用度、分、秒表示:78.43°.
解:∵78.43°=78°+0.43°,
0.43°=60′×0.43=25.8′,0.8′=60′×0.8=48″,
∴78.43°=78°25′48″.
新课讲解
(1)3.76°= 度 分 秒.
(2)上午10点30分时,时针与分针的夹角的度数是 .
练习
3
45
36
135°
要点1 角的概念
1. 有公共端点的 射线组成的图形叫做角,角也可以看作是一条射线绕着它的端点 而成的图形.
2. 角的表示方法:用三个 表示,顶点必须写在 ;用一个大写字母;一个数字或 字母.
要点1 1. 两条 旋转 2. 大写字母 中间 希腊
课堂练习
要点2 角的度量
1. 角的度量工具: .
2. 角的度量单位: 、 、 .
1周角= °,1平角= °,1°= ′,1′= ″.
要点2 1. 量角器 2. 度 分 秒 360 180 60 60
课堂练习
1. 一个齿轮板有36个齿,每相邻两齿中心线间的夹角都相等,这个夹角是( )
A. 36° B. 18° C.10° D. 42°
C
课堂练习
2. 已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是( )
A. ∠α=∠β B. ∠α<∠β C. ∠α=∠γ D. ∠β>∠γ
C
课堂练习
3. 下列能用∠1,∠AOB,∠O三种方法表示同一个角的图形是( )
A B C D
B
课堂练习
4. 如图所示,将一个矩形沿图中的虚线折叠,请用量角器量一下其中的α,β,得∠α ∠β.(填“>”“=”或“<”)
=
课堂练习
5.用度数表示下列各角度:
(1)37°54′; (2)45°12′;
(3)31°48′; (4)4°51′.
解:(1)54′=(54÷60)°=0.9°,即37°54′=37.9°.
(2)12″=(12÷60)°=0.2°,即45°12′=45.2°.
(3)48′=(48÷60)°=0.8°,即31°48′=31.8°.
(4)51′=(51÷60)°=0.85°,即4°51′=4.85°.
课堂练习
6.计算:180°-(38°45′+72.5°).
解:180°-(38°45′+72.5°)
=180°-(38°45′+72°30′),
=180°-111°15′,
=68°45′.
课堂练习
角的定义
有公共端点的两条射线组成的图形
一条射线绕着它的端点旋转而形成的图形
角的表示方法
用三个大写字母或一个大写字母表示
用一个数字加弧线表示
用一个小写希腊字母加弧线表示
角的度量
度、分、秒
1°=60′,1′=60″
课后总结
教材练习题1—3题.
布置作业
谢谢聆听
