人教版 九年级上数学 23.11 图形的旋转测试题(Word版 含答案)
文档属性
| 名称 | 人教版 九年级上数学 23.11 图形的旋转测试题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1007.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 17:01:54 | ||
图片预览




文档简介
人教版
九年级上数学
第23章23.1--23.2分节测试题含答案
23.1
图形的旋转
一、选择题
1.
如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4
cm,OB=1
cm,∠B′=60°,那么A′B的长是( )
A.4
cm
B.3
cm
C.2
cm
D.(4-)cm
2.
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A.
B.2
C.3
D.2
3.
2018·绵阳
在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )
A.(4,-3)
B.(-4,3)
C.(-3,4)
D.(-3,-4)
4.
如图,将线段AB先向右平移5个单位长度,再将所得线段绕原点顺时针旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )
A.(-4,1)
B.(-1,2)
C.(4,-1)
D.(1,-2)
5.
在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为( )
A.(,1)
B.(,-1)
C.(2,1)
D.(0,2)
6.
如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
A.(-1,2+)
B.(-,3)
C.(-,2+)
D.(-3,)
7.
如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
A.(,-1)
B.(1,-)
C.(2,0)
D.(,0)
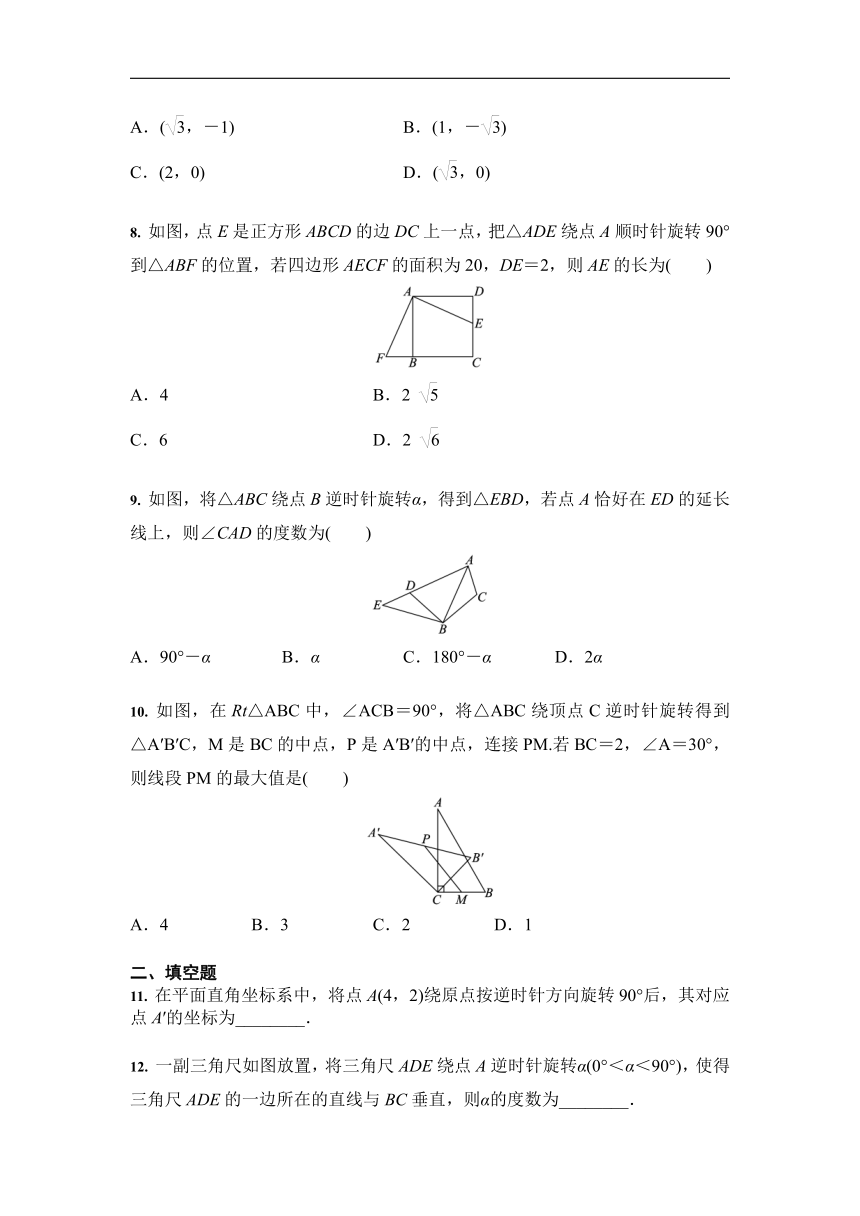
8.
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为( )
A.4
B.2
C.6
D.2
9.
如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α
B.α
C.180°-α
D.2α
10.
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM.若BC=2,∠A=30°,则线段PM的最大值是( )
A.4
B.3
C.2
D.1
二、填空题
11.
在平面直角坐标系中,将点A(4,2)绕原点按逆时针方向旋转90°后,其对应点A′的坐标为________.
12.
一副三角尺如图放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为________.
13.
把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.
14.
如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
15.
2018·陕西
如图,点O是平行四边形ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=AB;G,H是BC边上的点,且GH=BC.若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=________.
三、解答题
16.
如图,将一个钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得点C落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
17.
如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2;
(3)在(2)的条件下,求点A所经过的路径长(结果保留π).
18.
如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD′.
(1)求∠DAD′的度数;
(2)当∠DAE=45°时,求证:DE=D′E.
19.
如图,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D分别在OE和OF上,现将△OEF绕点O逆时针旋转角α(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=________;(用含α的式子表示)
(2)猜想图②中AF与DE的数量关系,并证明你的结论.
20.
已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD.
求证:BD2=AB2+BC2.
人教版
九年级数学
23.1
图形的旋转
针对训练
-答案
一、选择题
1.
【答案】B [解析]
∵旋转前、后的两个图形是全等图形,AB=4
cm,OB=1
cm,∴A′B′=AB=4
cm,OB′=OB=1
cm.
在△OB′B中,∵∠B′=60°,OB′=OB,
∴△OB′B是等边三角形,∴BB′=OB=1
cm,
∴A′B=A′B′-BB′=4-1=3(cm).
2.
【答案】A [解析]
∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5.
∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,
∴AE=4,DE=3,∴BE=1.
在Rt△BED中,BD==.故选A.
3.
【答案】B [解析]
如图所示,建立平面直角坐标系,点B的坐标为(-4,3).
4.
【答案】D
5.
【答案】A [解析]
如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,
∴∠AEO=∠A′FO=90°.
∵点A的坐标为(1,),∴AE=1,OE=,
∴OA=2,∠AOE=30°,由旋转可知∠AOA′=30°,OA′=OA=2,∴∠A′OF=90°-30°-30°=30°,∴A′F=OA′=1,OF=,∴A′(,1).
故选A.
6.
【答案】B
7.
【答案】A
8.
【答案】D [解析]
由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2
.
∵DE=2,∴在Rt△ADE中,AE==2
.故选D.
9.
【答案】C [解析]
由题意可得∠CBD=α,∠C=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠C+∠ADB=180°.
由四边形的内角和定理,得∠CAD+∠CBD=180°.
∴∠CAD=180°-∠CBD=180°-α.故选C.
10.
【答案】B [解析]
连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4.
根据旋转的性质可知,∠A′CB′=90°,A′B′=AB=4.
∵P是A′B′的中点,∴PC=A′B′=2.
∵M是BC的中点,∴CM=BC=1.
又∵PM≤PC+CM,
即PM≤3,
∴PM的最大值为3(此时点P,C,M共线).
故选B.
二、填空题
11.
【答案】(-2,4)
12.
【答案】15°或60° [解析]
分情况讨论:
①若DE⊥BC,设此时直线AD与BC交于点F,则∠BFA=90°-45°=45°,
∴∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;
②若AD⊥BC,则∠BAD=30°,∴α=90°-∠BAD=60°.
故答案为15°或60°.
13.
【答案】y=-x2-2x-3 [解析]
旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
14.
【答案】18 [解析]
如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
15.
【答案】 [解析]
∵==,==,
∴S1=S△AOB,S2=S△BOC.
∵点O是?ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD,∴=.
三、解答题
16.
【答案】
解:(1)旋转角的度数为60°.
(2)证明:由旋转的性质知∠ABC=∠A1BC1=120°,∠C=∠C1,AB=A1B.∵点A,B,C1在同一直线上,∴∠ABC1=180°,∴∠ABA1=∠CBC1=60°,∴∠A1BC=60°,
∵AB=A1B,∴△ABA1是等边三角形,
∴∠AA1B=∠A1BC=60°,
∴AA1∥BC,∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.
17.
【答案】
解:(1)如图.
(2)如图.
(3)如图,∵AO=A2O==,∠AOA2=90°,∴点A所经过的路径长=×2π=π.
18.
【答案】
解:(1)∵将△ABD绕点A逆时针旋转,得到△ACD′,
∴∠DAD′=∠BAC.
∵∠BAC=90°,∴∠DAD′=90°.
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°.
∵∠DAE=45°,
∴∠D′AE=∠DAD′-∠DAE=90°-45°=45°,
∴∠D′AE=∠DAE.
在△AED与△AED′中,
∴△AED≌△AED′(SAS),
∴DE=D′E.
19.
【答案】
解:(1)∵△OEF绕点O逆时针旋转角α,
∴∠DOF=∠COE=α.
∵四边形ABCD为正方形,
∴∠AOD=90°,
∴∠AOF=90°-α.
故答案为90°-α.
(2)猜想:AF=DE.
证明:∵四边形ABCD为正方形,
∴∠AOD=∠COD=90°,OA=OD.
∵∠DOF=∠COE=α,
∴∠AOF=∠DOE.
∵△OEF为等腰直角三角形,
∴OF=OE.
在△AOF和△DOE中,
∴△AOF≌△DOE(SAS),
∴AF=DE.
20.
【答案】
证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,
则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.
又∵∠ADC=60°,∴∠BDE=60°,
∴△DBE是等边三角形,
∴BD=BE.
又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,
∴△ECB是直角三角形,
∴BE2=CE2+BC2,即BD2=AB2+BC2.
23.2
中心对称
一、选择题
1.下面图形中,既是轴对称图形,又是中心对称图形的是
A.
B.
C.
D.
2.如图,,,若画一条直线将这个图形分成面积相等的两个部分,则符合要求的直线可以画(
)
A.条
B.条
C.条
D.无数条
3.如图,六边形ABCDEF的内角都相等,,则下列结论成立的个数是
;;;四边形ACDF是平行四边形;六边形ABCDEF既是中心对称图形,又是轴对称图形.
A.
2
B.
3
C.
4
D.
5
4、下列命题中真命题是(???
)
A、两个等腰三角形一定全等
B、正多边形的每一个内角的度数随边数增多而减少
C、菱形既是中心对称图形,又是轴对称图形
D、两直线平行,同旁内角相等
5.下列图形中,既是轴对称图形,又是中心对称图形的是(
)
A.
B.
C.
D.
6.下列图形中既是中心对称图形又是轴对称图形的是
A.
B.
C.
D.
7、下列图形中是轴对称而不是中心对称图形的是(????
)
A、平行四边形
B、线段
C、角
D、正方形
8.若点关于原点对称点的坐标为,则点的坐标是(
)
A.
B.
C.
D.
9、△ABC和△
关于点O对称,下列结论不正确的是(????
).
A、AO=
B、AB∥
?
C、CO=BO
D、∠BAC=∠
?
10、等边三角形与它本身重合,需绕着它的三边中线的交点旋转至少(???
).
A、60°
B、180°
C、360°
D、120°
11、关于成中心对称的两个图形的性质,下列说法正确的是(
)
A.
连接对应点的线段都经过对称中心,并且被对称中心平分
B.
成中心对称的两个图形的对应线段不一定相等
C.
对应点的连线不一定都经过对称中心
D.
以上说法都不对
12、如图是一个以为对称中心的中心对称图形,若,,,则的长为(
)
A.
4
B.
C.
D.
二、填空题
13、如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A?B?C?,则其旋转中心的坐标是 .
14.点A(-6,m)与点A′(n,3)关于原点中心对称,则m+n的值是____
.
15.在平面直角坐标系中,点关于原点对称的点的坐标是________.
16、关于中心对称的两个图形,对称点的连线经过________,并被________平分.
三、解答题
17、如图,画出△ABC关于点O中心对称的△A′B′C′.
18.如图,有四张背面完全相同的卡片,小伟将这四张卡片背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
用树状图或列表法表示两次摸出卡片所有可能出现的结果卡片可用表示;
求摸出两张卡片所表示的几何图形是轴对称图形而不是中心对称图形的概率.
19、请你把下面这个图形补画成中心对称图形,并且用点O表示对称中心(最少画三个)
.
20.在平面直角坐标系中,三个顶点的坐标分别是,,.
(1)将绕点旋转,请画出旋转后对应的△A1B1C;
(2)将△A1B1C沿着某个方向平移一定的距离后得到,已知点的对应点的坐标为,请画出平移后的;
(3)若与关于某一点中心对称,则对称中心的坐标为_____.
21、已知点A的坐标为(
,0),把点A绕着坐标原点顺时针旋转135?到点B,求点B的坐标.
22.
如图所示,△ABC中,M、N是边BC的三等分点,BE是AC边上的中线,连接AM、AN,分别交BE于F、G,求BF:FG:CE的值.
23、如图,在
中,
,
,将
绕点O沿逆时针方向旋转
得到
,连结
,求证:四边形
是平行四边形.
答案
1.
D
2.
D
3.
D
4、
C
5.
D
6.
C
7、
C
8.
B
9、
C
10、
D
11、
A
12、
D
13、
(1,-1)
14.
3
15.
16、
对称中心;对称中心
三、解答题
17、
如图所示,
18.
画树状图得:
则共有16种等可能的结果;
是轴对称图形而不是中心对称图形情况数C、C,
是轴对称图形而不是中心对称图形的概率.??
19、
20.
(1)△A1B1C1如图所示;
(2)△A2B2C2,如图所示;
(3)∵,,,,,
∴与关于原点对,对称中心坐标为,
21、
解:把A(
,0)绕坐标原点顺时针旋转135°到点B,则点B在第三象限且与y轴夹角为45°,所以点B的坐标为(-1,-1).
22.
解:如答图所示.
作已知图形的中心对称图形,以E为对称中心.令BF=a,FG=b,GE=c.
因为M′C∥AM,N′C∥AN
所以a:(2b+2c)=BM:MC=1:2
所以a=b+c,而(a+b):2c=BN:NC=2:1所以:a+b=4c,所以a=c,b=c.
所以BF:FG:GE=5:3:2.
23、
证明:∵在
中,
,
,∴
,结合图形旋转的性质可知:
,
,
,
,∴
,∵
,∴四边形
是平行四边形.
九年级上数学
第23章23.1--23.2分节测试题含答案
23.1
图形的旋转
一、选择题
1.
如图,将△OAB绕点O逆时针旋转得到△OA′B′,使点B恰好落在边A′B′上.已知AB=4
cm,OB=1
cm,∠B′=60°,那么A′B的长是( )
A.4
cm
B.3
cm
C.2
cm
D.(4-)cm
2.
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )
A.
B.2
C.3
D.2
3.
2018·绵阳
在平面直角坐标系中,以原点为旋转中心,把点A(3,4)逆时针旋转90°,得到点B,则点B的坐标为( )
A.(4,-3)
B.(-4,3)
C.(-3,4)
D.(-3,-4)
4.
如图,将线段AB先向右平移5个单位长度,再将所得线段绕原点顺时针旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )
A.(-4,1)
B.(-1,2)
C.(4,-1)
D.(1,-2)
5.
在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A顺时针旋转30°得到点A′,则点A′的坐标为( )
A.(,1)
B.(,-1)
C.(2,1)
D.(0,2)
6.
如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是( )
A.(-1,2+)
B.(-,3)
C.(-,2+)
D.(-3,)
7.
如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
A.(,-1)
B.(1,-)
C.(2,0)
D.(,0)
8.
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为( )
A.4
B.2
C.6
D.2
9.
如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α
B.α
C.180°-α
D.2α
10.
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM.若BC=2,∠A=30°,则线段PM的最大值是( )
A.4
B.3
C.2
D.1
二、填空题
11.
在平面直角坐标系中,将点A(4,2)绕原点按逆时针方向旋转90°后,其对应点A′的坐标为________.
12.
一副三角尺如图放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为________.
13.
把二次函数y=(x-1)2+2的图象绕原点旋转180°后得到的图象的解析式为_______.
14.
如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为________.
15.
2018·陕西
如图,点O是平行四边形ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=AB;G,H是BC边上的点,且GH=BC.若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=________.
三、解答题
16.
如图,将一个钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得点C落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
17.
如图,在正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2;
(3)在(2)的条件下,求点A所经过的路径长(结果保留π).
18.
如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD′.
(1)求∠DAD′的度数;
(2)当∠DAE=45°时,求证:DE=D′E.
19.
如图,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D分别在OE和OF上,现将△OEF绕点O逆时针旋转角α(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=________;(用含α的式子表示)
(2)猜想图②中AF与DE的数量关系,并证明你的结论.
20.
已知:如图,在四边形ABCD中,∠ADC=60°,∠ABC=30°,AD=CD.
求证:BD2=AB2+BC2.
人教版
九年级数学
23.1
图形的旋转
针对训练
-答案
一、选择题
1.
【答案】B [解析]
∵旋转前、后的两个图形是全等图形,AB=4
cm,OB=1
cm,∴A′B′=AB=4
cm,OB′=OB=1
cm.
在△OB′B中,∵∠B′=60°,OB′=OB,
∴△OB′B是等边三角形,∴BB′=OB=1
cm,
∴A′B=A′B′-BB′=4-1=3(cm).
2.
【答案】A [解析]
∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=5.
∵将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,
∴AE=4,DE=3,∴BE=1.
在Rt△BED中,BD==.故选A.
3.
【答案】B [解析]
如图所示,建立平面直角坐标系,点B的坐标为(-4,3).
4.
【答案】D
5.
【答案】A [解析]
如图,过点A作AE⊥y轴于点E,过点A′作A′F⊥x轴于点F,
∴∠AEO=∠A′FO=90°.
∵点A的坐标为(1,),∴AE=1,OE=,
∴OA=2,∠AOE=30°,由旋转可知∠AOA′=30°,OA′=OA=2,∴∠A′OF=90°-30°-30°=30°,∴A′F=OA′=1,OF=,∴A′(,1).
故选A.
6.
【答案】B
7.
【答案】A
8.
【答案】D [解析]
由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2
.
∵DE=2,∴在Rt△ADE中,AE==2
.故选D.
9.
【答案】C [解析]
由题意可得∠CBD=α,∠C=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠C+∠ADB=180°.
由四边形的内角和定理,得∠CAD+∠CBD=180°.
∴∠CAD=180°-∠CBD=180°-α.故选C.
10.
【答案】B [解析]
连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4.
根据旋转的性质可知,∠A′CB′=90°,A′B′=AB=4.
∵P是A′B′的中点,∴PC=A′B′=2.
∵M是BC的中点,∴CM=BC=1.
又∵PM≤PC+CM,
即PM≤3,
∴PM的最大值为3(此时点P,C,M共线).
故选B.
二、填空题
11.
【答案】(-2,4)
12.
【答案】15°或60° [解析]
分情况讨论:
①若DE⊥BC,设此时直线AD与BC交于点F,则∠BFA=90°-45°=45°,
∴∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;
②若AD⊥BC,则∠BAD=30°,∴α=90°-∠BAD=60°.
故答案为15°或60°.
13.
【答案】y=-x2-2x-3 [解析]
旋转前二次项的系数a=1,抛物线的顶点坐标是(1,2),旋转后二次项的系数a=-1,抛物线的顶点坐标是(-1,-2),∴新抛物线的解析式为y=-(x+1)2-2,即y=-x2-2x-3.
14.
【答案】18 [解析]
如图.∵∠BAD=∠BCD=90°,∴∠B+∠ADC=180°.又∵AB=AD,∴将△ABC绕点A逆时针旋转90°后点B与点D重合,点C的对应点E落在CD的延长线上,∴AE=AC=6,∠CAE=90°,∴S四边形ABCD=S△ACE=AC·AE=×6×6=18.
15.
【答案】 [解析]
∵==,==,
∴S1=S△AOB,S2=S△BOC.
∵点O是?ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD,∴=.
三、解答题
16.
【答案】
解:(1)旋转角的度数为60°.
(2)证明:由旋转的性质知∠ABC=∠A1BC1=120°,∠C=∠C1,AB=A1B.∵点A,B,C1在同一直线上,∴∠ABC1=180°,∴∠ABA1=∠CBC1=60°,∴∠A1BC=60°,
∵AB=A1B,∴△ABA1是等边三角形,
∴∠AA1B=∠A1BC=60°,
∴AA1∥BC,∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.
17.
【答案】
解:(1)如图.
(2)如图.
(3)如图,∵AO=A2O==,∠AOA2=90°,∴点A所经过的路径长=×2π=π.
18.
【答案】
解:(1)∵将△ABD绕点A逆时针旋转,得到△ACD′,
∴∠DAD′=∠BAC.
∵∠BAC=90°,∴∠DAD′=90°.
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°.
∵∠DAE=45°,
∴∠D′AE=∠DAD′-∠DAE=90°-45°=45°,
∴∠D′AE=∠DAE.
在△AED与△AED′中,
∴△AED≌△AED′(SAS),
∴DE=D′E.
19.
【答案】
解:(1)∵△OEF绕点O逆时针旋转角α,
∴∠DOF=∠COE=α.
∵四边形ABCD为正方形,
∴∠AOD=90°,
∴∠AOF=90°-α.
故答案为90°-α.
(2)猜想:AF=DE.
证明:∵四边形ABCD为正方形,
∴∠AOD=∠COD=90°,OA=OD.
∵∠DOF=∠COE=α,
∴∠AOF=∠DOE.
∵△OEF为等腰直角三角形,
∴OF=OE.
在△AOF和△DOE中,
∴△AOF≌△DOE(SAS),
∴AF=DE.
20.
【答案】
证明:如图,将△ADB绕点D顺时针旋转60°,得到△CDE,连接BE,
则∠ADB=∠CDE,∠A=∠DCE,AB=CE,BD=DE.
又∵∠ADC=60°,∴∠BDE=60°,
∴△DBE是等边三角形,
∴BD=BE.
又∵∠ECB=360°-∠BCD-∠DCE=360°-∠BCD-∠A=360°-(360°-∠ADC-∠ABC)=90°,
∴△ECB是直角三角形,
∴BE2=CE2+BC2,即BD2=AB2+BC2.
23.2
中心对称
一、选择题
1.下面图形中,既是轴对称图形,又是中心对称图形的是
A.
B.
C.
D.
2.如图,,,若画一条直线将这个图形分成面积相等的两个部分,则符合要求的直线可以画(
)
A.条
B.条
C.条
D.无数条
3.如图,六边形ABCDEF的内角都相等,,则下列结论成立的个数是
;;;四边形ACDF是平行四边形;六边形ABCDEF既是中心对称图形,又是轴对称图形.
A.
2
B.
3
C.
4
D.
5
4、下列命题中真命题是(???
)
A、两个等腰三角形一定全等
B、正多边形的每一个内角的度数随边数增多而减少
C、菱形既是中心对称图形,又是轴对称图形
D、两直线平行,同旁内角相等
5.下列图形中,既是轴对称图形,又是中心对称图形的是(
)
A.
B.
C.
D.
6.下列图形中既是中心对称图形又是轴对称图形的是
A.
B.
C.
D.
7、下列图形中是轴对称而不是中心对称图形的是(????
)
A、平行四边形
B、线段
C、角
D、正方形
8.若点关于原点对称点的坐标为,则点的坐标是(
)
A.
B.
C.
D.
9、△ABC和△
关于点O对称,下列结论不正确的是(????
).
A、AO=
B、AB∥
?
C、CO=BO
D、∠BAC=∠
?
10、等边三角形与它本身重合,需绕着它的三边中线的交点旋转至少(???
).
A、60°
B、180°
C、360°
D、120°
11、关于成中心对称的两个图形的性质,下列说法正确的是(
)
A.
连接对应点的线段都经过对称中心,并且被对称中心平分
B.
成中心对称的两个图形的对应线段不一定相等
C.
对应点的连线不一定都经过对称中心
D.
以上说法都不对
12、如图是一个以为对称中心的中心对称图形,若,,,则的长为(
)
A.
4
B.
C.
D.
二、填空题
13、如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A?B?C?,则其旋转中心的坐标是 .
14.点A(-6,m)与点A′(n,3)关于原点中心对称,则m+n的值是____
.
15.在平面直角坐标系中,点关于原点对称的点的坐标是________.
16、关于中心对称的两个图形,对称点的连线经过________,并被________平分.
三、解答题
17、如图,画出△ABC关于点O中心对称的△A′B′C′.
18.如图,有四张背面完全相同的卡片,小伟将这四张卡片背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
用树状图或列表法表示两次摸出卡片所有可能出现的结果卡片可用表示;
求摸出两张卡片所表示的几何图形是轴对称图形而不是中心对称图形的概率.
19、请你把下面这个图形补画成中心对称图形,并且用点O表示对称中心(最少画三个)
.
20.在平面直角坐标系中,三个顶点的坐标分别是,,.
(1)将绕点旋转,请画出旋转后对应的△A1B1C;
(2)将△A1B1C沿着某个方向平移一定的距离后得到,已知点的对应点的坐标为,请画出平移后的;
(3)若与关于某一点中心对称,则对称中心的坐标为_____.
21、已知点A的坐标为(
,0),把点A绕着坐标原点顺时针旋转135?到点B,求点B的坐标.
22.
如图所示,△ABC中,M、N是边BC的三等分点,BE是AC边上的中线,连接AM、AN,分别交BE于F、G,求BF:FG:CE的值.
23、如图,在
中,
,
,将
绕点O沿逆时针方向旋转
得到
,连结
,求证:四边形
是平行四边形.
答案
1.
D
2.
D
3.
D
4、
C
5.
D
6.
C
7、
C
8.
B
9、
C
10、
D
11、
A
12、
D
13、
(1,-1)
14.
3
15.
16、
对称中心;对称中心
三、解答题
17、
如图所示,
18.
画树状图得:
则共有16种等可能的结果;
是轴对称图形而不是中心对称图形情况数C、C,
是轴对称图形而不是中心对称图形的概率.??
19、
20.
(1)△A1B1C1如图所示;
(2)△A2B2C2,如图所示;
(3)∵,,,,,
∴与关于原点对,对称中心坐标为,
21、
解:把A(
,0)绕坐标原点顺时针旋转135°到点B,则点B在第三象限且与y轴夹角为45°,所以点B的坐标为(-1,-1).
22.
解:如答图所示.
作已知图形的中心对称图形,以E为对称中心.令BF=a,FG=b,GE=c.
因为M′C∥AM,N′C∥AN
所以a:(2b+2c)=BM:MC=1:2
所以a=b+c,而(a+b):2c=BN:NC=2:1所以:a+b=4c,所以a=c,b=c.
所以BF:FG:GE=5:3:2.
23、
证明:∵在
中,
,
,∴
,结合图形旋转的性质可知:
,
,
,
,∴
,∵
,∴四边形
是平行四边形.
同课章节目录
