人教版数学七年级上册 4.1几何图形同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级上册 4.1几何图形同步测试题(一)(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 19:35:48 | ||
图片预览

文档简介
几何图形同步测试题(一)
一.选择题
1.用一个平面去截一个圆柱体,截面图形不可能是( )
A.长方形
B.梯形
C.圆形
D.椭圆形
2.如图是正方体的展开图,则原正方体相对两个面上的数字和最小是( )
A.8
B.7
C.6
D.4
3.如图,是一个五棱柱形的几何体,下列关于该几何体的叙述正确的是( )
A.有4条侧棱
B.有5个面
C.有10条棱
D.有10个顶点
4.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )
A.
B.
C.
D.
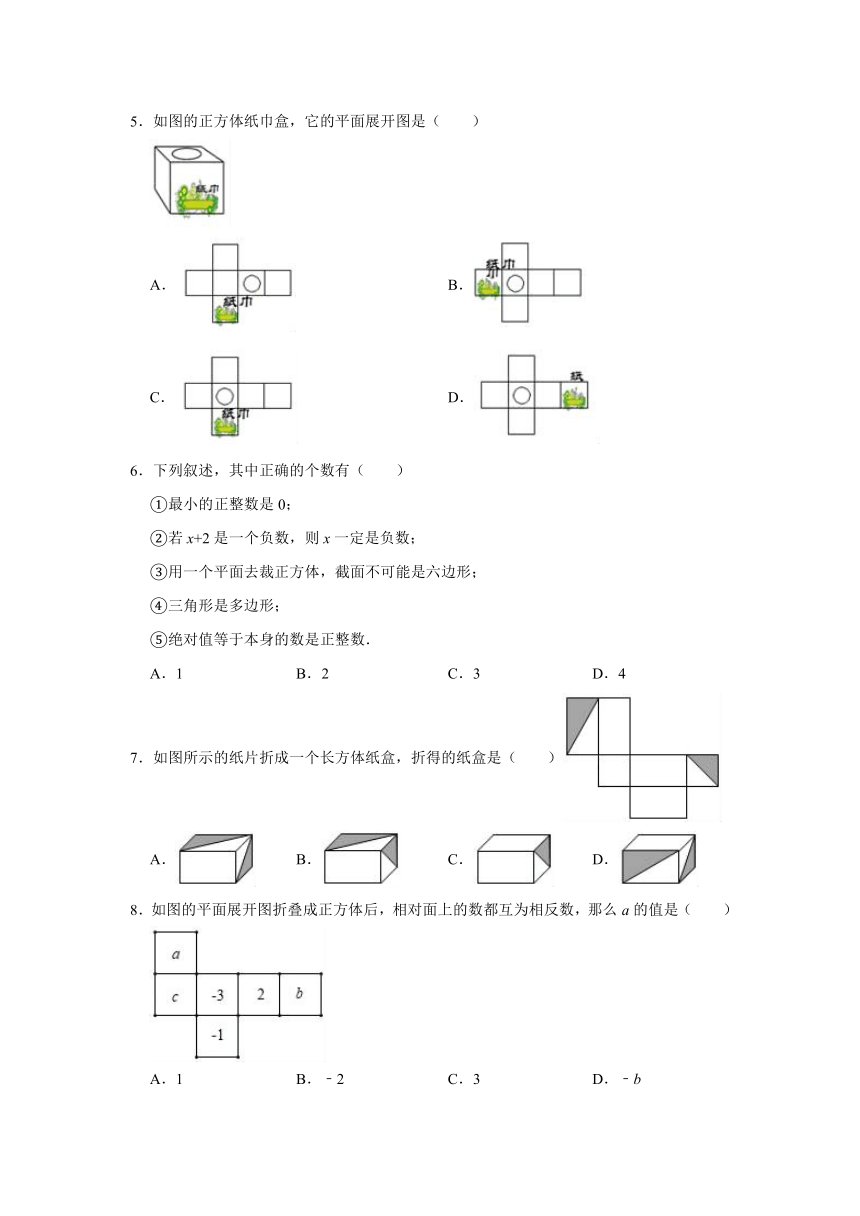
5.如图的正方体纸巾盒,它的平面展开图是( )
A.
B.
C.
D.
6.下列叙述,其中正确的个数有( )
①最小的正整数是0;
②若x+2是一个负数,则x一定是负数;
③用一个平面去裁正方体,截面不可能是六边形;
④三角形是多边形;
⑤绝对值等于本身的数是正整数.
A.1
B.2
C.3
D.4
7.如图所示的纸片折成一个长方体纸盒,折得的纸盒是( )
A.
B.
C.
D.
8.如图的平面展开图折叠成正方体后,相对面上的数都互为相反数,那么a的值是( )
A.1
B.﹣2
C.3
D.﹣b
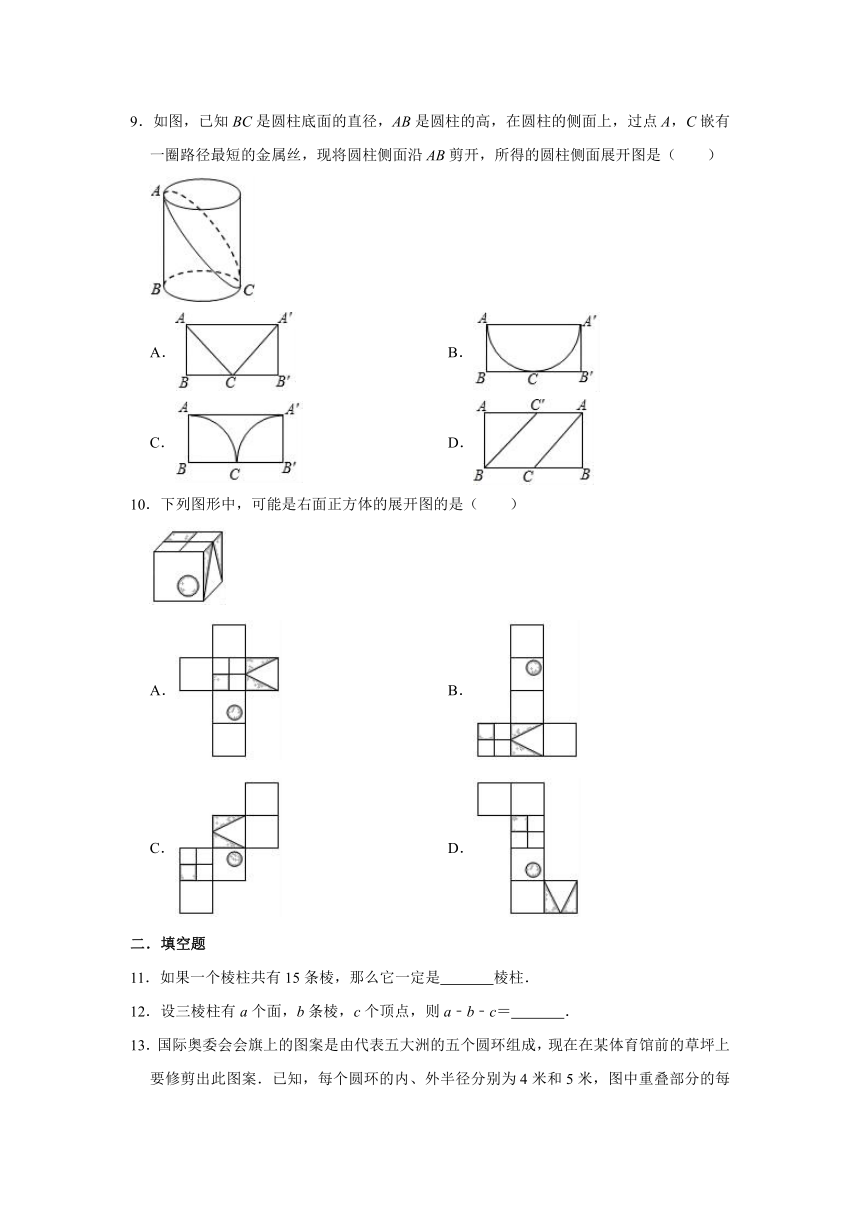
9.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A.
B.
C.
D.
10.下列图形中,可能是右面正方体的展开图的是( )
A.
B.
C.
D.
二.填空题
11.如果一个棱柱共有15条棱,那么它一定是
棱柱.
12.设三棱柱有a个面,b条棱,c个顶点,则a﹣b﹣c=
.
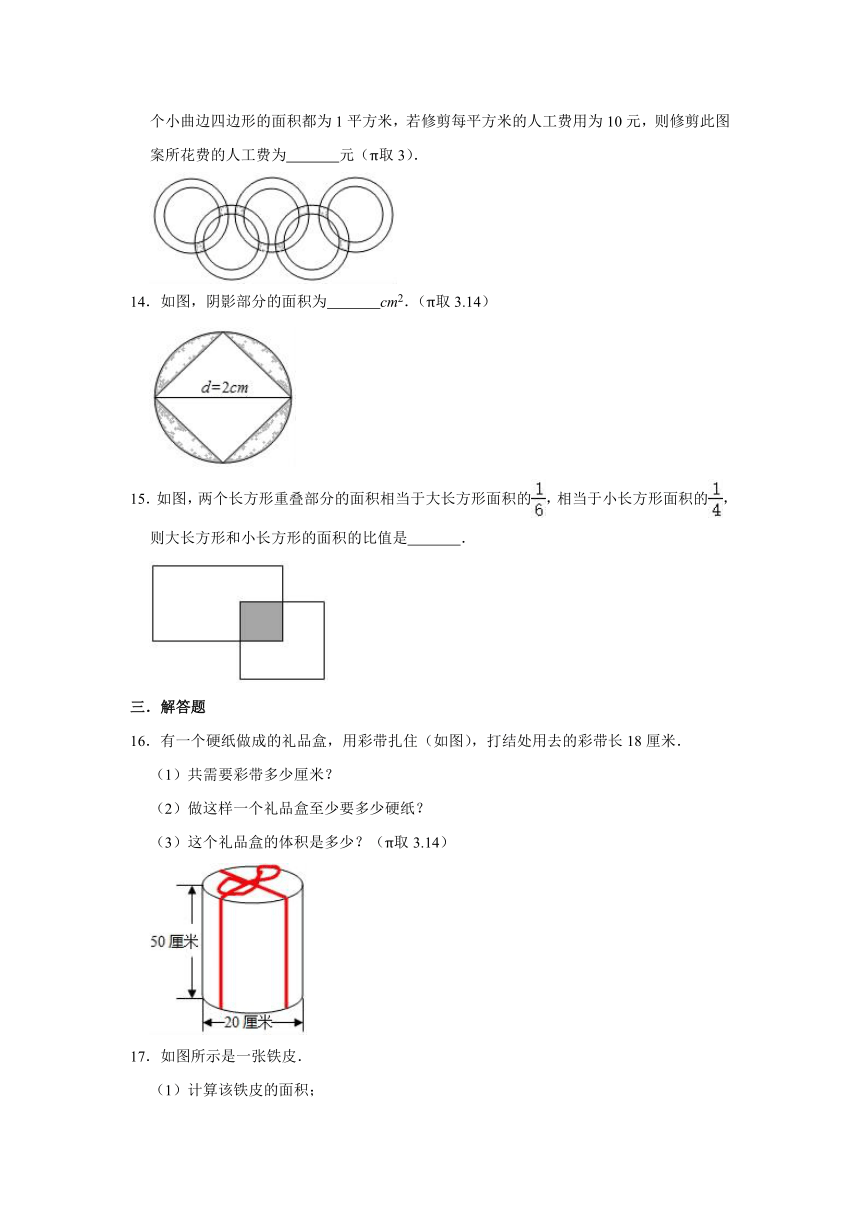
13.国际奥委会会旗上的图案是由代表五大洲的五个圆环组成,现在在某体育馆前的草坪上要修剪出此图案.已知,每个圆环的内、外半径分别为4米和5米,图中重叠部分的每个小曲边四边形的面积都为1平方米,若修剪每平方米的人工费用为10元,则修剪此图案所花费的人工费为
元(π取3).
14.如图,阴影部分的面积为
cm2.(π取3.14)
15.如图,两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,则大长方形和小长方形的面积的比值是
.
三.解答题
16.有一个硬纸做成的礼品盒,用彩带扎住(如图),打结处用去的彩带长18厘米.
(1)共需要彩带多少厘米?
(2)做这样一个礼品盒至少要多少硬纸?
(3)这个礼品盒的体积是多少?(π取3.14)
17.如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)它能否做成一个长方体盒子?若能,画出来,计算它的体积;若不能,说明理由.
18.随着城市的发展,住宅小区的建设也越来越人性化.为响应国家“加强全民健身设施建设,发展全民体育”的号召.哈市某小区在一片足够大的空地中,改建出一个休闲广场,规划设计如图所示.求塑胶地面休闲区的面积;
(2)求广场中种植花卉的面积与种植草坪的面积的比值.
19.如图①所示,从大正方体中截去一个小正方体之后,可以得到图②的几何体.
(1)设原大正方体的表面积为a,图②中几何体的表面积为b,那么a与b的大小关系是
;
A.a>b;B.a<b;C.a=b;D.无法判断.
(2)小明说“设图①中大正方体的棱长之和为m,图②中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图③是图②几何体的表面展开图吗?如有错误,请予修正.
参考答案与试题解析
一.选择题
1.【解答】解:用一个平面去截一个圆柱体,
截面图形可能是:长方形、正方形,圆形,椭圆形,
但不可能是梯形.
故选:B.
2.【解答】解:易得2和6是相对的两个面;3和4是相对两个面;1和5是相对的两个面,
所以原正方体相对两个面上的数字和最小的是6,
故选:C.
3.【解答】解:图中几何体是正五棱柱,五棱柱有
7个面,10个顶点,5条侧棱,15条棱.
故选:D.
4.【解答】解:A、不能折叠成正方体,故选项错误;
B、不能折成圆锥,故选项错误;
C、能折成圆柱,故选项正确;
D、不能折成三棱柱,故选项错误.
故选:C.
5.【解答】解:观察图形可知,正方体纸巾盒的平面展开图是:
故选:C.
6.【解答】解:①最小的正整数是1,此结论错误;
②若x+2是一个负数,则x一定是负数是正确的;
③用一个平面去截正方体,截面与六个面均相交即可得六边形,此结论错误;
④三角形是多边形是正确的;
⑤绝对值等于本身的数是正数和0,此结论错误.
故正确的个数有2个.
故选:B.
7.【解答】解:如图所示:
根据题意可知,A的对面是A′,B的对面是B′,C的对面是C′,A的短边阴影与C的阴影重合.
故用形如图所示的纸片折成一个长方体纸盒,折得的纸盒是C.
故选:C.
8.【解答】解:“a”与“﹣1”相对,
∵相对面上的两个数都互为相反数,
∴a=1.
故选:A.
9.【解答】解:因圆柱的展开面为长方形,AC展开应该是两线段,且有公共点C.
故选:A.
10.【解答】解:A、折叠后,圆不是与两个空白小正方形相邻,故与原正方体不符,故此选项错误;
B、折叠后,圆与三角形成对面,与原正方体不符,故此选项错误;
C、折叠后与原正方体相同,与原正方体符合,故此选项正确;
D、折叠后,两个三角形的短边不是与两个空白小正方形相邻,与原正方体不符,故此选项错误.
故选:C.
二.填空题(共5小题)
11.【解答】解:15÷3=5,
所以是五棱柱,
故答案为:五.
12.【解答】解:三棱柱有5个面,9条棱,6个顶点,
因此a=5,b=9,c=6,
所以a﹣b﹣c=5﹣9﹣6=﹣10,
故答案为:﹣10.
13.【解答】解:修剪草坪的面积为:(π×52﹣π×42)×5﹣1×8=45π﹣8≈127(平方米),
因此所用的人工费为10×127=1270(元),
故答案为:1270.
14.【解答】解:S阴影=S圆形﹣S正方形=π×()2﹣×2×2=π﹣2≈1.14(cm2),
故答案为:1.14.
15.【解答】解:设阴影部分的面积为k,
∵阴影部分的面积相当于大长方形面积的,相当于小长方形面积的,
∴大长方形的面积为6k,小长方形的面积为4k,
∴大长方形和小长方形的面积的比值为=,
故答案为:.
三.解答题(共4小题)
16.【解答】解:(1)50×4+20×4+18=298(cm),
(2)π×()2×2+π×20×50=200π+1000π=1200π(cm2),
(3)π×()2×50=5000π≈15700(cm3),
答:做这样一个礼品盒共需要彩带298厘米;至少要1200π平方厘米的硬纸;这个礼品盒的体积约为15700立方厘米.
17.【解答】解:(1)(1×3+2×3+1×2)×2=22(m2),
(2)根据棱柱的展开与折叠,可得可以折叠成长方体的盒子,其长、宽、高分别为3cm,2cm,1cm,
因此体积为:1×2×3=6(m3),
18.【解答】解:(1)S塑胶地面=S长方形+S半圆=10×20+π×()2=200+50π≈350(平方米),
答:塑胶地面休闲区的面积为350平方米;
(2)S种花卉=S长方形﹣S半圆=200﹣150=50(平方米),
S种草坪=S半圆=50π≈150(平方米),
所以,广场中种植花卉的面积与种植草坪的面积的比值为=.
19.【解答】解:(1)根据“切去三个小面”但又“新增三个小面”,因此与原来的表面积相等,即a=b,
故答案为:C;
(2)如图②红颜色的棱是多出来的,共6条,
如果截去的小正方体的棱长为大正方体的棱长的一半时,n比m正好多出大正方体的3条棱的长度,
如果截去的小正方体的棱长不是大正方体的棱长的一半,n比m就不是多出大正方体的
一.选择题
1.用一个平面去截一个圆柱体,截面图形不可能是( )
A.长方形
B.梯形
C.圆形
D.椭圆形
2.如图是正方体的展开图,则原正方体相对两个面上的数字和最小是( )
A.8
B.7
C.6
D.4
3.如图,是一个五棱柱形的几何体,下列关于该几何体的叙述正确的是( )
A.有4条侧棱
B.有5个面
C.有10条棱
D.有10个顶点
4.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )
A.
B.
C.
D.
5.如图的正方体纸巾盒,它的平面展开图是( )
A.
B.
C.
D.
6.下列叙述,其中正确的个数有( )
①最小的正整数是0;
②若x+2是一个负数,则x一定是负数;
③用一个平面去裁正方体,截面不可能是六边形;
④三角形是多边形;
⑤绝对值等于本身的数是正整数.
A.1
B.2
C.3
D.4
7.如图所示的纸片折成一个长方体纸盒,折得的纸盒是( )
A.
B.
C.
D.
8.如图的平面展开图折叠成正方体后,相对面上的数都互为相反数,那么a的值是( )
A.1
B.﹣2
C.3
D.﹣b
9.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A.
B.
C.
D.
10.下列图形中,可能是右面正方体的展开图的是( )
A.
B.
C.
D.
二.填空题
11.如果一个棱柱共有15条棱,那么它一定是
棱柱.
12.设三棱柱有a个面,b条棱,c个顶点,则a﹣b﹣c=
.
13.国际奥委会会旗上的图案是由代表五大洲的五个圆环组成,现在在某体育馆前的草坪上要修剪出此图案.已知,每个圆环的内、外半径分别为4米和5米,图中重叠部分的每个小曲边四边形的面积都为1平方米,若修剪每平方米的人工费用为10元,则修剪此图案所花费的人工费为
元(π取3).
14.如图,阴影部分的面积为
cm2.(π取3.14)
15.如图,两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,则大长方形和小长方形的面积的比值是
.
三.解答题
16.有一个硬纸做成的礼品盒,用彩带扎住(如图),打结处用去的彩带长18厘米.
(1)共需要彩带多少厘米?
(2)做这样一个礼品盒至少要多少硬纸?
(3)这个礼品盒的体积是多少?(π取3.14)
17.如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)它能否做成一个长方体盒子?若能,画出来,计算它的体积;若不能,说明理由.
18.随着城市的发展,住宅小区的建设也越来越人性化.为响应国家“加强全民健身设施建设,发展全民体育”的号召.哈市某小区在一片足够大的空地中,改建出一个休闲广场,规划设计如图所示.求塑胶地面休闲区的面积;
(2)求广场中种植花卉的面积与种植草坪的面积的比值.
19.如图①所示,从大正方体中截去一个小正方体之后,可以得到图②的几何体.
(1)设原大正方体的表面积为a,图②中几何体的表面积为b,那么a与b的大小关系是
;
A.a>b;B.a<b;C.a=b;D.无法判断.
(2)小明说“设图①中大正方体的棱长之和为m,图②中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图③是图②几何体的表面展开图吗?如有错误,请予修正.
参考答案与试题解析
一.选择题
1.【解答】解:用一个平面去截一个圆柱体,
截面图形可能是:长方形、正方形,圆形,椭圆形,
但不可能是梯形.
故选:B.
2.【解答】解:易得2和6是相对的两个面;3和4是相对两个面;1和5是相对的两个面,
所以原正方体相对两个面上的数字和最小的是6,
故选:C.
3.【解答】解:图中几何体是正五棱柱,五棱柱有
7个面,10个顶点,5条侧棱,15条棱.
故选:D.
4.【解答】解:A、不能折叠成正方体,故选项错误;
B、不能折成圆锥,故选项错误;
C、能折成圆柱,故选项正确;
D、不能折成三棱柱,故选项错误.
故选:C.
5.【解答】解:观察图形可知,正方体纸巾盒的平面展开图是:
故选:C.
6.【解答】解:①最小的正整数是1,此结论错误;
②若x+2是一个负数,则x一定是负数是正确的;
③用一个平面去截正方体,截面与六个面均相交即可得六边形,此结论错误;
④三角形是多边形是正确的;
⑤绝对值等于本身的数是正数和0,此结论错误.
故正确的个数有2个.
故选:B.
7.【解答】解:如图所示:
根据题意可知,A的对面是A′,B的对面是B′,C的对面是C′,A的短边阴影与C的阴影重合.
故用形如图所示的纸片折成一个长方体纸盒,折得的纸盒是C.
故选:C.
8.【解答】解:“a”与“﹣1”相对,
∵相对面上的两个数都互为相反数,
∴a=1.
故选:A.
9.【解答】解:因圆柱的展开面为长方形,AC展开应该是两线段,且有公共点C.
故选:A.
10.【解答】解:A、折叠后,圆不是与两个空白小正方形相邻,故与原正方体不符,故此选项错误;
B、折叠后,圆与三角形成对面,与原正方体不符,故此选项错误;
C、折叠后与原正方体相同,与原正方体符合,故此选项正确;
D、折叠后,两个三角形的短边不是与两个空白小正方形相邻,与原正方体不符,故此选项错误.
故选:C.
二.填空题(共5小题)
11.【解答】解:15÷3=5,
所以是五棱柱,
故答案为:五.
12.【解答】解:三棱柱有5个面,9条棱,6个顶点,
因此a=5,b=9,c=6,
所以a﹣b﹣c=5﹣9﹣6=﹣10,
故答案为:﹣10.
13.【解答】解:修剪草坪的面积为:(π×52﹣π×42)×5﹣1×8=45π﹣8≈127(平方米),
因此所用的人工费为10×127=1270(元),
故答案为:1270.
14.【解答】解:S阴影=S圆形﹣S正方形=π×()2﹣×2×2=π﹣2≈1.14(cm2),
故答案为:1.14.
15.【解答】解:设阴影部分的面积为k,
∵阴影部分的面积相当于大长方形面积的,相当于小长方形面积的,
∴大长方形的面积为6k,小长方形的面积为4k,
∴大长方形和小长方形的面积的比值为=,
故答案为:.
三.解答题(共4小题)
16.【解答】解:(1)50×4+20×4+18=298(cm),
(2)π×()2×2+π×20×50=200π+1000π=1200π(cm2),
(3)π×()2×50=5000π≈15700(cm3),
答:做这样一个礼品盒共需要彩带298厘米;至少要1200π平方厘米的硬纸;这个礼品盒的体积约为15700立方厘米.
17.【解答】解:(1)(1×3+2×3+1×2)×2=22(m2),
(2)根据棱柱的展开与折叠,可得可以折叠成长方体的盒子,其长、宽、高分别为3cm,2cm,1cm,
因此体积为:1×2×3=6(m3),
18.【解答】解:(1)S塑胶地面=S长方形+S半圆=10×20+π×()2=200+50π≈350(平方米),
答:塑胶地面休闲区的面积为350平方米;
(2)S种花卉=S长方形﹣S半圆=200﹣150=50(平方米),
S种草坪=S半圆=50π≈150(平方米),
所以,广场中种植花卉的面积与种植草坪的面积的比值为=.
19.【解答】解:(1)根据“切去三个小面”但又“新增三个小面”,因此与原来的表面积相等,即a=b,
故答案为:C;
(2)如图②红颜色的棱是多出来的,共6条,
如果截去的小正方体的棱长为大正方体的棱长的一半时,n比m正好多出大正方体的3条棱的长度,
如果截去的小正方体的棱长不是大正方体的棱长的一半,n比m就不是多出大正方体的
