人教版数学九年级上册 第23章 旋转 23.1图形的旋转同步测试试题(一)(word解析版)
文档属性
| 名称 | 人教版数学九年级上册 第23章 旋转 23.1图形的旋转同步测试试题(一)(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 254.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 13:50:12 | ||
图片预览




文档简介
图形的旋转同步测试试题(一)
一.选择题
1.将图绕其中心旋转某一角度后会与原图形重合,这个角不能是( )
A.90° B.120° C.180° D.270°
2.如图,在△ABC中,∠B=50°,将△ABC绕点A按逆时针方向旋转得到△A′B′C′.若点B′恰好落在BC边上,则∠CB′C′的度数为( )
A.50° B.60° C.80° D.100°
3.如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD,若AD∥BC,则∠ABE的度数为( )
A.25° B.30° C.35° D.40°
4.如图,将直角三角形AOB绕点O旋转得到直角三角形COD,若∠AOB=90°,∠BOC=130°,则∠AOD的度数为( )
A.40° B.50° C.60° D.30°
5.如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
A.3 B.4 C.5 D.4
6.如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
A.50° B.60° C.40° D.30°
7.如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )
A.12 B.4 C.8 D.6
8.如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
A.BE=CE B.FM=MC C.AM⊥FC D.BF⊥CF
9.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC绕点A顺时针旋转90°得到(点D与点B是对应点,点E与点C是对应点),连接CE,则∠CED的度数是( )
A.45° B.30° C.25° D.15°
10.如图,将△AOB绕点O按逆时针方向旋转55°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
A.25° B.30° C.35° D.40°
二.填空题
11.如图,已知点D为等边三角形ABC的AC边的中点,BC=4,点B绕着点D顺时针旋转180°的过程中,点B的对应点为点B',连接B'C、B'D,当△B'DC的面积为时,∠B'DB为 .
12.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为 .
13.如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,则∠A的度数是 .
14.如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD,把△ABC绕点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,则m= .
15.如图,P为等边△ABC内一点,∠APC=150°,且∠APD=30°,AP=6,CP=3,DP=7,则BD的长为 .
三.解答题
16.如图,在△ABC中,∠C=90°,∠CAB=20°,BC=7;线段AD是由线段AC绕点A按逆时针方向旋转110°得到,△EFG是由△ABC沿CB方向平移得到,且直线EF过点D
(1)求∠DAE的大小.
(2)求DE的长.
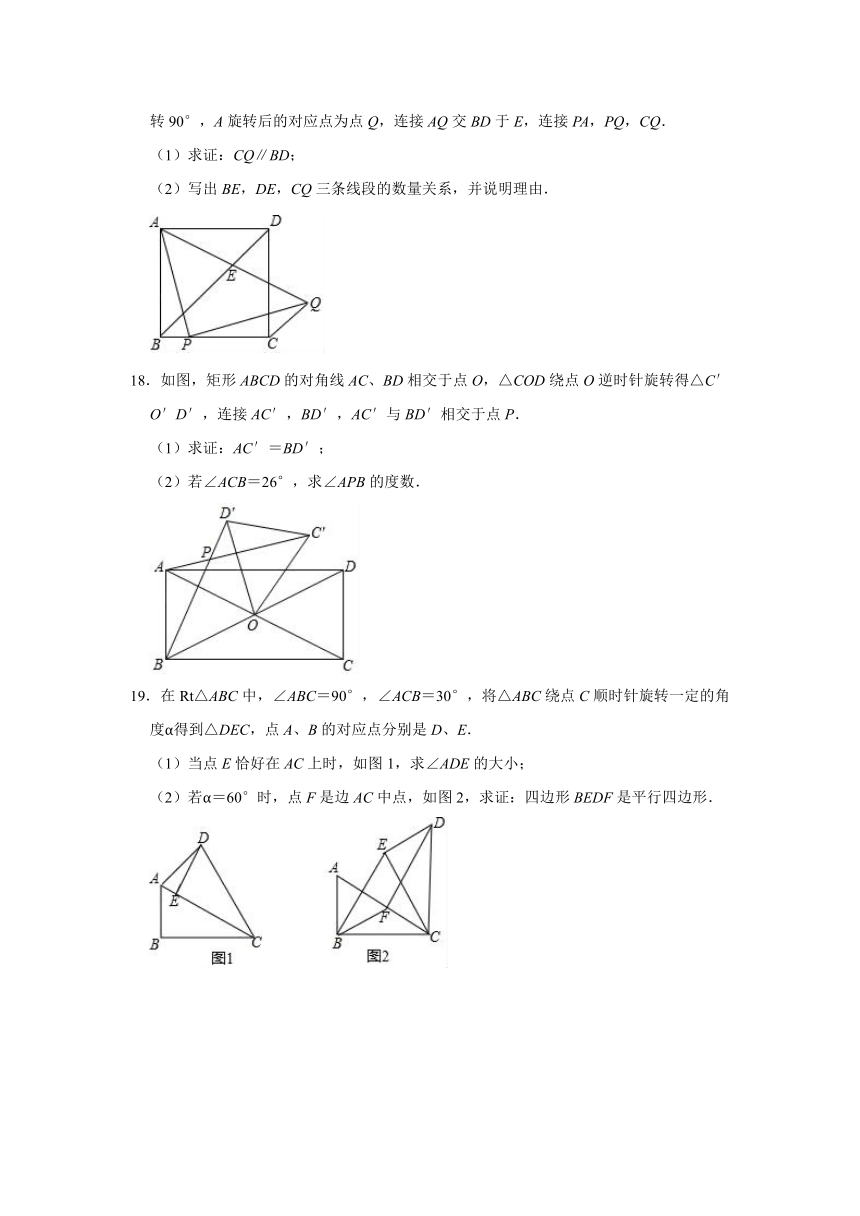
17.如图,P是正方形ABCD的BC边上的一动点,P与B不重合,将点A绕点P顺时针旋转90°,A旋转后的对应点为点Q,连接AQ交BD于E,连接PA,PQ,CQ.
(1)求证:CQ∥BD;
(2)写出BE,DE,CQ三条线段的数量关系,并说明理由.
18.如图,矩形ABCD的对角线AC、BD相交于点O,△COD绕点O逆时针旋转得△C′O′D′,连接AC′,BD′,AC′与BD′相交于点P.
(1)求证:AC′=BD′;
(2)若∠ACB=26°,求∠APB的度数.
19.在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
(1)当点E恰好在AC上时,如图1,求∠ADE的大小;
(2)若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.
参考答案与试题解析
一.选择题
1.【解答】解:图形可看作由一个基本图形旋转90°所组成,故最小旋转角为90°.
则该图形绕其中心旋转90°n(n取1,2,3…)后会与原图形重合.
故这个角不能是120°.
故选:B.
2.【解答】解:∵将△ABC绕点A按逆时针方向旋转得到△A′B′C′,
∴AB=AB′,∠C′B′A=∠B,
∴∠AB′B=∠B,
∵∠B=50°,
∴∠C′B′A=∠AB′B=50°,
∴∠CB′C′=180°﹣∠C′B′A﹣∠AB′B=80°,
故选:C.
3.【解答】解:∵将△ABC绕点B按逆时针方向旋转40°,
∴AB=DB,∠ABD=∠CBE=40°,
∴∠BAD=∠BDA=70°,
∵AD∥BC,
∴∠DAB=∠ABC=70°,
∴∠ABE=∠ABC﹣∠EBC=30°,
故选:B.
4.【解答】解:由旋转的性质可知:∠AOC=∠BOD,
∵∠AOB=90°,∠BOC=∠AOB+∠AOC=130°,
∴∠BOD=∠AOC=∠BOC﹣∠AOB=40°,
又∵∠BOD+∠AOD=∠AOB=90°,
∴∠AOD=50°,
故选:B.
5.【解答】解:如图所示:过点F作FG⊥AC.
∵由旋转的性质可知:CE=BC=4,CD=AC=6,∠ECD=∠BCA=90°.
∴AE=AC﹣CE=2.
∵FG⊥AC,CD⊥AC,
∴FG∥CD.
又∵F是ED的中点,
∴G是CE的中点,
∴EG=2,FG=CD=3.
∴AG=AE+EG=4.
∴AF==5.
故选:C.
6.【解答】解:∵将△OAB绕点O逆时针旋转80°
∴∠A=∠C,∠AOC=80°
∴∠DOC=80°﹣α
∵∠A=2∠D=100°
∴∠D=50°
∵∠C+∠D+∠DOC=180°
∴100°+50°+80°﹣α=180° 解得α=50°
故选:A.
7.【解答】解:∵旋转后AC的中点恰好与D点重合,即AD=AC′=AC,
∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,
∴∠DAD′=60°,
∴∠DAE=30°,
∴∠EAC=∠ACD=30°,
∴AE=CE,
在Rt△ADE中,设AE=EC=x,则有DE=DC﹣EC=AB﹣EC=6﹣x,AD=×6=2,
根据勾股定理得:x2=(6﹣x)2+(2)2,
解得:x=4,
∴EC=4,
则S△AEC=ECAD=4.
故选:B.
8.【解答】解:因为E是BC上任意一点,E不一定是BC的中点,故选项A错误;
根据旋转的性质可得△ABE≌△CBF,则∠AEB=∠F,
又∵直角△ABE中,∠BAE+∠AEB=90°,
∴∠BAE+∠F=90°,
∴∠AMF=90°,
∴AM⊥FC,故C正确;
E是BC上任意一点,BF=BE,则AC和AF不一定相等,则M不一定是FC的中点,则B错误;
∵BF⊥BC,
∴BF⊥CF一定错误,故D错误.
故选:C.
9.【解答】解:∵△ADE可以由△ABC绕点A顺时针旋转90°得到,
∴△ADE≌△ABC,
∴AE=AC,∠DAE=∠BAC=90°,
∴△CAE为等腰直角三角形,则∠CEA=45°.
∵Rt△ABC中,∠BAC=90°,∠B=60°,
∴∠BCA=30°,
∴∠DEA=∠BCA=30°.
∴∠CED=∠CEA﹣∠DEA=45°﹣30°=15°.
故选:D.
10.【解答】解:∵△AOB绕点O按逆时针方向旋转55°后得到△A′OB′,
∴∠BOB′=55°,
∴∠AOB′=∠BOB′﹣∠AOB=55°﹣15°=40°.
故选:D.
二.填空题(共5小题)
11.【解答】解:如图,若点B'在AC的左侧时,过点B'作BN⊥AC,交CA于点N,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC=4,
又∵点D是CD的中点,
∴BD⊥AC,CD=AD=2,BD=CD=2,
∵△B'DC的面积为,
∴×CD×B'N=,
∴×2×B'N=,
∴B'N=,
∵点B绕着点D顺时针旋转180°,
∴B'D=BD=2,
∴DN===,
∴DN=B'N=,
∴∠NDB'=∠DB'N=45°,
∴∠BDB'=45°,
在点B'在AC的右侧时,∠B''DA=45°,
∴∠BDB''=135°,
综上所述:∠B'DB=45°或135°,
故答案为:45°或135°.
12.【解答】解:∵把△ADE顺时针旋转△ABF的位置,
∴△ADE的面积=△ABF的面积,
∴四边形AECF的面积等于正方形ABCD的面积等于25,
∴AD=DC=5,
∵DE=2,
∴Rt△ADE中,AE===,
故答案为:.
13.【解答】解:∵△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
∴∠AOC=∠BOD=40°,OA=OC,
∵OA=OC,
∴∠A=∠OCA,
∴∠A=(180°﹣40°)=70°,
故答案为:70°.
14.【解答】解:①当点B落在AB边上时,
∵DB=DB1,
∴∠B=∠DB1B=40°,
∴m=∠BDB1=180°﹣2×40°=100°,
②当点B落在AC上时,
在Rt△DCB2中,
∵∠C=90°,DB2=DB=2CD,
∴∠CB2D=30°,
∴m=∠C+∠CB2D=120°,
综上所述,m的值为100°或120°.
故答案为:100°或120°.
15.【解答】解:把△APC绕点C逆时针旋转60°得△BEC,连接PE,如图所示:
则△BEC≌△APC,
∴CE=CP,∠PCE=60°,BE=AP=6,∠BEC=∠APC=150°,
∴△PCE是等边三角形,
∴∠EPC=∠PEC=60°,PE=CP=3,
∴∠BED=∠BEC﹣∠PEC=90°,
∵∠APD=30°,
∴∠DPC=150°﹣30°=120°,
又∵∠DPE=∠DPC+∠EPC=120°+60°=180°,
即D、P、E在同一条直线上,
∴DE=DP+PE=7+3=10,
在Rt△BDE中,BD==2,
即BD的长为2,
故答案为:2.
三.解答题(共4小题)
16.【解答】解:(1)∵△EFG是由△ABC沿CB方向平移得到
∴AE∥CF,EF∥AB
∴∠C+∠EAC=180°,∠C=90°
∴∠EAC=90°
∵线段AD是由线段AC绕点A按逆时针方向旋转110°得到
∴∠DAC=110°,AD=AC
∴∠DAE=20°
(2)∵AE∥CF,EF∥AB
∴∠ABC=∠EAB,∠EAB=∠DEA
∴∠DEA=∠ABC,且∠DAE=∠BAC=20°,AD=AC
∴△DAE≌△CAB(AAS)
∴DE=BC=7
17.【解答】解:(1)证明:作PF⊥BC交BD于F,连接FQ,FA,DQ,
∵四边形ABCD是正方形,
∴∠PBF=∠ABF=∠ABC=45°,AD∥BC,AD=BC=BA,
∴∠PFB=90°﹣∠PBF=45°,
∴∠PBF=∠PFB,
∴PB=PF,∠BPA=∠FPQ=90°﹣∠APF,
又PA=PQ
∴△ABP≌△QFP(SAS),
∴BA=FQ,∠PFQ=∠PBA=90°,
∴FQ=BC,∠PFQ=∠FPB=90°,
∴FQ∥BC,
∴四边形BCQF为平行四边形,
∴CQ∥BD;
(2)BE,DE,CQ三条线段的数量关系是BE=CQ+DE,理由如下:
由(1)得,四边形BCQF为平行四边形,
∴CQ=BF,FQ∥BC,FQ=BC,
又AD∥BC,AD=BC,
∴FQ=AD,FQ∥AD,
∴四边形ADQF为平行四边形,
∴DE=EF,
∴BE=BF+EF=CQ+DE.
18.【解答】(1)证明:∵四边形ABCD是矩形
∴OA=OC=AC,OB=OD=BD,AC=BD
∴OA=OC=OB=OD
∵△COD绕点O逆时针旋转得△C′O′D′,
∴OC′=OC,OD′=OD,∠D′OC′=∠DOC=∠BOA
∴OB=OA,OD′=OC′,∠BOD′=∠AOC′=∠AOB+∠AOD′
∴△BOD′≌△AOC′(SAS)
∴AC'=BD’
(2)
由(1)得△BOD′≌△AOC′,OC=OB
∴∠OBD′=∠OAC′,∠OBC=∠ACB=26°
又∠BEO=∠AEP
∴∠APB=∠AOB=∠OBC+∠ACB=26°+26°=52°
19.【解答】(1)解:如图1,∵△ABC绕点C顺时针旋转α得到△DEC,点E恰好在AC上,
∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,
∵CA=CD,
∴∠CAD=∠CDA=(180°﹣30°)=75°,
∴∠ADE=90°﹣75°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=AC,
∵∠ACB=30°,
∴AB=AC,
∴BF=AB,
∵△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,DE=AB,
∴DE=BF,△ACD和△BCE为等边三角形,
∴BE=CB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△CFD≌△ABC
一.选择题
1.将图绕其中心旋转某一角度后会与原图形重合,这个角不能是( )
A.90° B.120° C.180° D.270°
2.如图,在△ABC中,∠B=50°,将△ABC绕点A按逆时针方向旋转得到△A′B′C′.若点B′恰好落在BC边上,则∠CB′C′的度数为( )
A.50° B.60° C.80° D.100°
3.如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD,若AD∥BC,则∠ABE的度数为( )
A.25° B.30° C.35° D.40°
4.如图,将直角三角形AOB绕点O旋转得到直角三角形COD,若∠AOB=90°,∠BOC=130°,则∠AOD的度数为( )
A.40° B.50° C.60° D.30°
5.如图,在Rt△ABC中,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF的长为( )
A.3 B.4 C.5 D.4
6.如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
A.50° B.60° C.40° D.30°
7.如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )
A.12 B.4 C.8 D.6
8.如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
A.BE=CE B.FM=MC C.AM⊥FC D.BF⊥CF
9.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC绕点A顺时针旋转90°得到(点D与点B是对应点,点E与点C是对应点),连接CE,则∠CED的度数是( )
A.45° B.30° C.25° D.15°
10.如图,将△AOB绕点O按逆时针方向旋转55°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
A.25° B.30° C.35° D.40°
二.填空题
11.如图,已知点D为等边三角形ABC的AC边的中点,BC=4,点B绕着点D顺时针旋转180°的过程中,点B的对应点为点B',连接B'C、B'D,当△B'DC的面积为时,∠B'DB为 .
12.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为25,DE=2,则AE的长为 .
13.如图,△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,则∠A的度数是 .
14.如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD,把△ABC绕点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,则m= .
15.如图,P为等边△ABC内一点,∠APC=150°,且∠APD=30°,AP=6,CP=3,DP=7,则BD的长为 .
三.解答题
16.如图,在△ABC中,∠C=90°,∠CAB=20°,BC=7;线段AD是由线段AC绕点A按逆时针方向旋转110°得到,△EFG是由△ABC沿CB方向平移得到,且直线EF过点D
(1)求∠DAE的大小.
(2)求DE的长.
17.如图,P是正方形ABCD的BC边上的一动点,P与B不重合,将点A绕点P顺时针旋转90°,A旋转后的对应点为点Q,连接AQ交BD于E,连接PA,PQ,CQ.
(1)求证:CQ∥BD;
(2)写出BE,DE,CQ三条线段的数量关系,并说明理由.
18.如图,矩形ABCD的对角线AC、BD相交于点O,△COD绕点O逆时针旋转得△C′O′D′,连接AC′,BD′,AC′与BD′相交于点P.
(1)求证:AC′=BD′;
(2)若∠ACB=26°,求∠APB的度数.
19.在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
(1)当点E恰好在AC上时,如图1,求∠ADE的大小;
(2)若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.
参考答案与试题解析
一.选择题
1.【解答】解:图形可看作由一个基本图形旋转90°所组成,故最小旋转角为90°.
则该图形绕其中心旋转90°n(n取1,2,3…)后会与原图形重合.
故这个角不能是120°.
故选:B.
2.【解答】解:∵将△ABC绕点A按逆时针方向旋转得到△A′B′C′,
∴AB=AB′,∠C′B′A=∠B,
∴∠AB′B=∠B,
∵∠B=50°,
∴∠C′B′A=∠AB′B=50°,
∴∠CB′C′=180°﹣∠C′B′A﹣∠AB′B=80°,
故选:C.
3.【解答】解:∵将△ABC绕点B按逆时针方向旋转40°,
∴AB=DB,∠ABD=∠CBE=40°,
∴∠BAD=∠BDA=70°,
∵AD∥BC,
∴∠DAB=∠ABC=70°,
∴∠ABE=∠ABC﹣∠EBC=30°,
故选:B.
4.【解答】解:由旋转的性质可知:∠AOC=∠BOD,
∵∠AOB=90°,∠BOC=∠AOB+∠AOC=130°,
∴∠BOD=∠AOC=∠BOC﹣∠AOB=40°,
又∵∠BOD+∠AOD=∠AOB=90°,
∴∠AOD=50°,
故选:B.
5.【解答】解:如图所示:过点F作FG⊥AC.
∵由旋转的性质可知:CE=BC=4,CD=AC=6,∠ECD=∠BCA=90°.
∴AE=AC﹣CE=2.
∵FG⊥AC,CD⊥AC,
∴FG∥CD.
又∵F是ED的中点,
∴G是CE的中点,
∴EG=2,FG=CD=3.
∴AG=AE+EG=4.
∴AF==5.
故选:C.
6.【解答】解:∵将△OAB绕点O逆时针旋转80°
∴∠A=∠C,∠AOC=80°
∴∠DOC=80°﹣α
∵∠A=2∠D=100°
∴∠D=50°
∵∠C+∠D+∠DOC=180°
∴100°+50°+80°﹣α=180° 解得α=50°
故选:A.
7.【解答】解:∵旋转后AC的中点恰好与D点重合,即AD=AC′=AC,
∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,
∴∠DAD′=60°,
∴∠DAE=30°,
∴∠EAC=∠ACD=30°,
∴AE=CE,
在Rt△ADE中,设AE=EC=x,则有DE=DC﹣EC=AB﹣EC=6﹣x,AD=×6=2,
根据勾股定理得:x2=(6﹣x)2+(2)2,
解得:x=4,
∴EC=4,
则S△AEC=ECAD=4.
故选:B.
8.【解答】解:因为E是BC上任意一点,E不一定是BC的中点,故选项A错误;
根据旋转的性质可得△ABE≌△CBF,则∠AEB=∠F,
又∵直角△ABE中,∠BAE+∠AEB=90°,
∴∠BAE+∠F=90°,
∴∠AMF=90°,
∴AM⊥FC,故C正确;
E是BC上任意一点,BF=BE,则AC和AF不一定相等,则M不一定是FC的中点,则B错误;
∵BF⊥BC,
∴BF⊥CF一定错误,故D错误.
故选:C.
9.【解答】解:∵△ADE可以由△ABC绕点A顺时针旋转90°得到,
∴△ADE≌△ABC,
∴AE=AC,∠DAE=∠BAC=90°,
∴△CAE为等腰直角三角形,则∠CEA=45°.
∵Rt△ABC中,∠BAC=90°,∠B=60°,
∴∠BCA=30°,
∴∠DEA=∠BCA=30°.
∴∠CED=∠CEA﹣∠DEA=45°﹣30°=15°.
故选:D.
10.【解答】解:∵△AOB绕点O按逆时针方向旋转55°后得到△A′OB′,
∴∠BOB′=55°,
∴∠AOB′=∠BOB′﹣∠AOB=55°﹣15°=40°.
故选:D.
二.填空题(共5小题)
11.【解答】解:如图,若点B'在AC的左侧时,过点B'作BN⊥AC,交CA于点N,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,AB=AC=BC=4,
又∵点D是CD的中点,
∴BD⊥AC,CD=AD=2,BD=CD=2,
∵△B'DC的面积为,
∴×CD×B'N=,
∴×2×B'N=,
∴B'N=,
∵点B绕着点D顺时针旋转180°,
∴B'D=BD=2,
∴DN===,
∴DN=B'N=,
∴∠NDB'=∠DB'N=45°,
∴∠BDB'=45°,
在点B'在AC的右侧时,∠B''DA=45°,
∴∠BDB''=135°,
综上所述:∠B'DB=45°或135°,
故答案为:45°或135°.
12.【解答】解:∵把△ADE顺时针旋转△ABF的位置,
∴△ADE的面积=△ABF的面积,
∴四边形AECF的面积等于正方形ABCD的面积等于25,
∴AD=DC=5,
∵DE=2,
∴Rt△ADE中,AE===,
故答案为:.
13.【解答】解:∵△COD是△AOB绕点O顺时针方向旋转40°后所得的图形,点C恰好在AB上,
∴∠AOC=∠BOD=40°,OA=OC,
∵OA=OC,
∴∠A=∠OCA,
∴∠A=(180°﹣40°)=70°,
故答案为:70°.
14.【解答】解:①当点B落在AB边上时,
∵DB=DB1,
∴∠B=∠DB1B=40°,
∴m=∠BDB1=180°﹣2×40°=100°,
②当点B落在AC上时,
在Rt△DCB2中,
∵∠C=90°,DB2=DB=2CD,
∴∠CB2D=30°,
∴m=∠C+∠CB2D=120°,
综上所述,m的值为100°或120°.
故答案为:100°或120°.
15.【解答】解:把△APC绕点C逆时针旋转60°得△BEC,连接PE,如图所示:
则△BEC≌△APC,
∴CE=CP,∠PCE=60°,BE=AP=6,∠BEC=∠APC=150°,
∴△PCE是等边三角形,
∴∠EPC=∠PEC=60°,PE=CP=3,
∴∠BED=∠BEC﹣∠PEC=90°,
∵∠APD=30°,
∴∠DPC=150°﹣30°=120°,
又∵∠DPE=∠DPC+∠EPC=120°+60°=180°,
即D、P、E在同一条直线上,
∴DE=DP+PE=7+3=10,
在Rt△BDE中,BD==2,
即BD的长为2,
故答案为:2.
三.解答题(共4小题)
16.【解答】解:(1)∵△EFG是由△ABC沿CB方向平移得到
∴AE∥CF,EF∥AB
∴∠C+∠EAC=180°,∠C=90°
∴∠EAC=90°
∵线段AD是由线段AC绕点A按逆时针方向旋转110°得到
∴∠DAC=110°,AD=AC
∴∠DAE=20°
(2)∵AE∥CF,EF∥AB
∴∠ABC=∠EAB,∠EAB=∠DEA
∴∠DEA=∠ABC,且∠DAE=∠BAC=20°,AD=AC
∴△DAE≌△CAB(AAS)
∴DE=BC=7
17.【解答】解:(1)证明:作PF⊥BC交BD于F,连接FQ,FA,DQ,
∵四边形ABCD是正方形,
∴∠PBF=∠ABF=∠ABC=45°,AD∥BC,AD=BC=BA,
∴∠PFB=90°﹣∠PBF=45°,
∴∠PBF=∠PFB,
∴PB=PF,∠BPA=∠FPQ=90°﹣∠APF,
又PA=PQ
∴△ABP≌△QFP(SAS),
∴BA=FQ,∠PFQ=∠PBA=90°,
∴FQ=BC,∠PFQ=∠FPB=90°,
∴FQ∥BC,
∴四边形BCQF为平行四边形,
∴CQ∥BD;
(2)BE,DE,CQ三条线段的数量关系是BE=CQ+DE,理由如下:
由(1)得,四边形BCQF为平行四边形,
∴CQ=BF,FQ∥BC,FQ=BC,
又AD∥BC,AD=BC,
∴FQ=AD,FQ∥AD,
∴四边形ADQF为平行四边形,
∴DE=EF,
∴BE=BF+EF=CQ+DE.
18.【解答】(1)证明:∵四边形ABCD是矩形
∴OA=OC=AC,OB=OD=BD,AC=BD
∴OA=OC=OB=OD
∵△COD绕点O逆时针旋转得△C′O′D′,
∴OC′=OC,OD′=OD,∠D′OC′=∠DOC=∠BOA
∴OB=OA,OD′=OC′,∠BOD′=∠AOC′=∠AOB+∠AOD′
∴△BOD′≌△AOC′(SAS)
∴AC'=BD’
(2)
由(1)得△BOD′≌△AOC′,OC=OB
∴∠OBD′=∠OAC′,∠OBC=∠ACB=26°
又∠BEO=∠AEP
∴∠APB=∠AOB=∠OBC+∠ACB=26°+26°=52°
19.【解答】(1)解:如图1,∵△ABC绕点C顺时针旋转α得到△DEC,点E恰好在AC上,
∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,
∵CA=CD,
∴∠CAD=∠CDA=(180°﹣30°)=75°,
∴∠ADE=90°﹣75°=15°;
(2)证明:如图2,
∵点F是边AC中点,
∴BF=AC,
∵∠ACB=30°,
∴AB=AC,
∴BF=AB,
∵△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,DE=AB,
∴DE=BF,△ACD和△BCE为等边三角形,
∴BE=CB,
∵点F为△ACD的边AC的中点,
∴DF⊥AC,
易证得△CFD≌△ABC
同课章节目录
