人教版数学九年级上册 第23章旋转 23.2中心对称同步测试试题(一)(word解析版)
文档属性
| 名称 | 人教版数学九年级上册 第23章旋转 23.2中心对称同步测试试题(一)(word解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 314.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 13:51:33 | ||
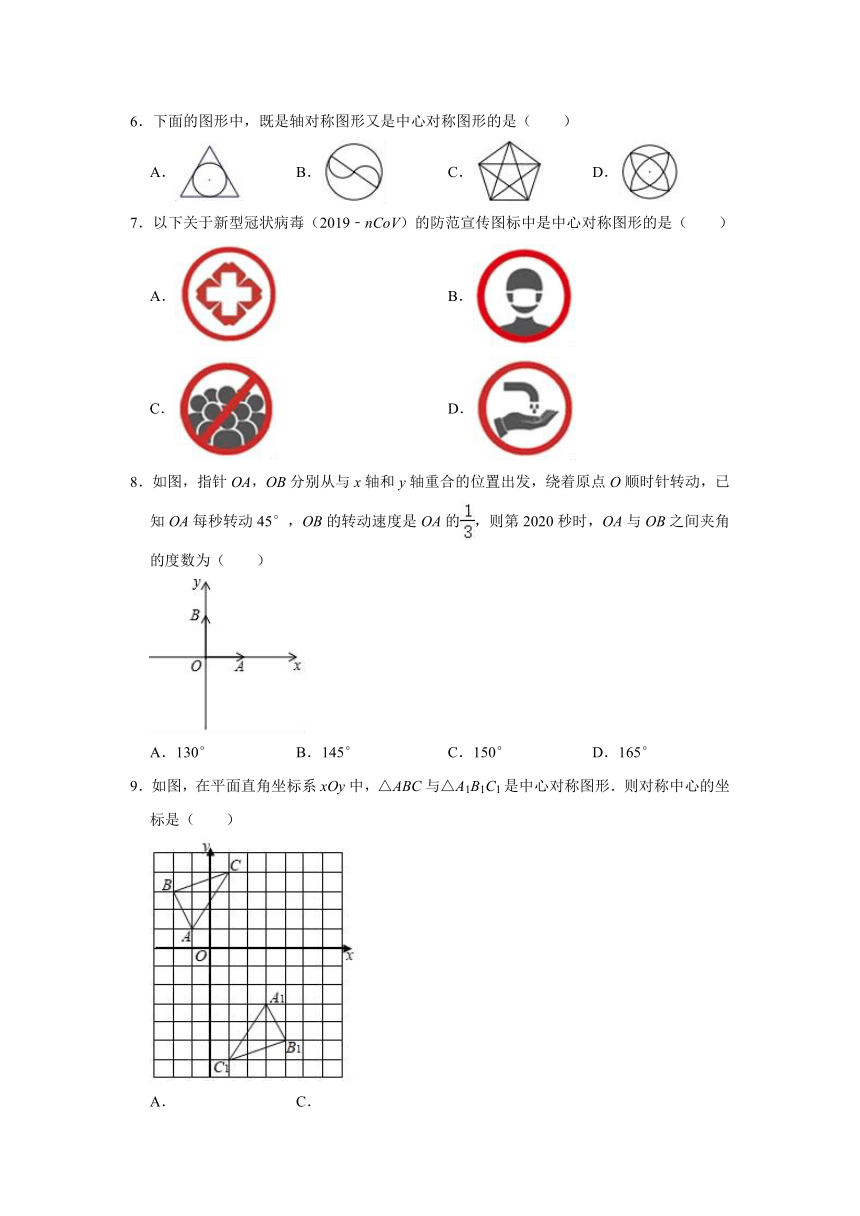
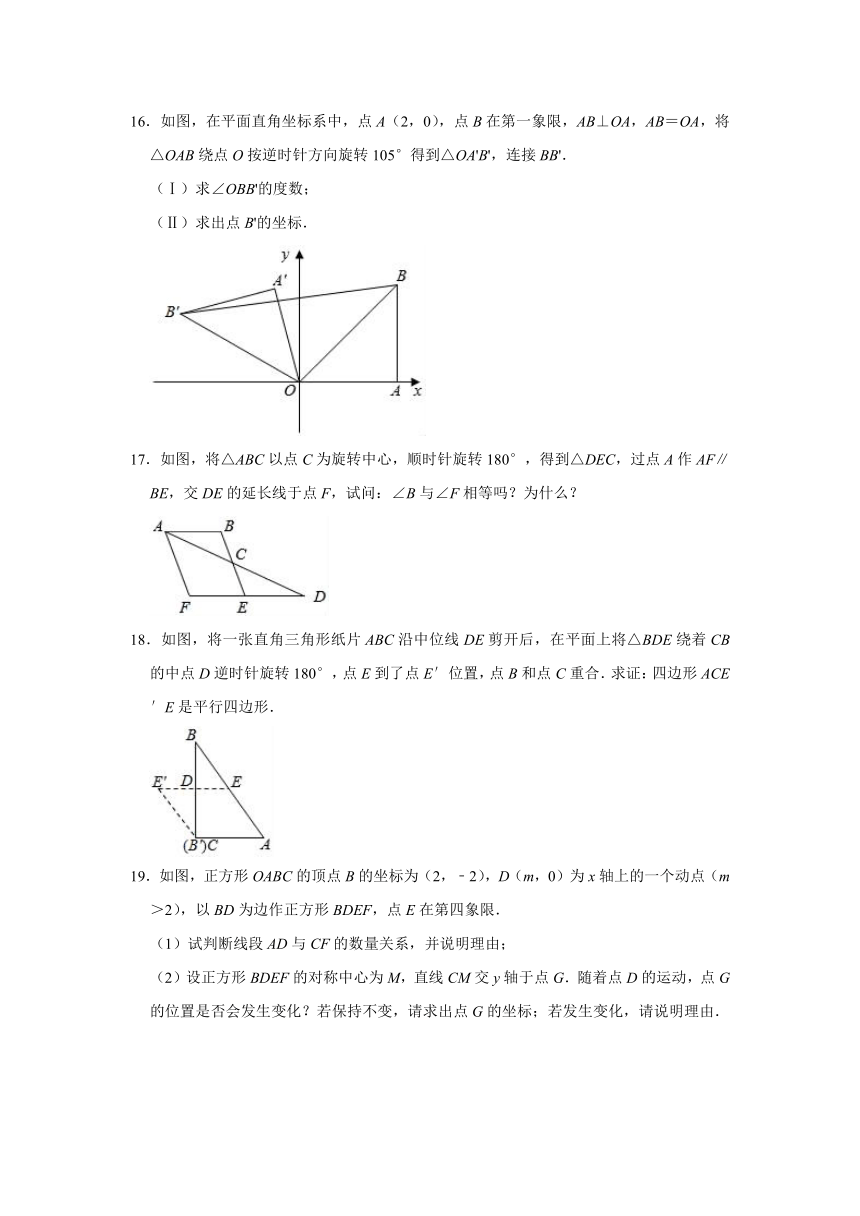
图片预览


文档简介
中心对称同步测试试题(一)
一.选择题
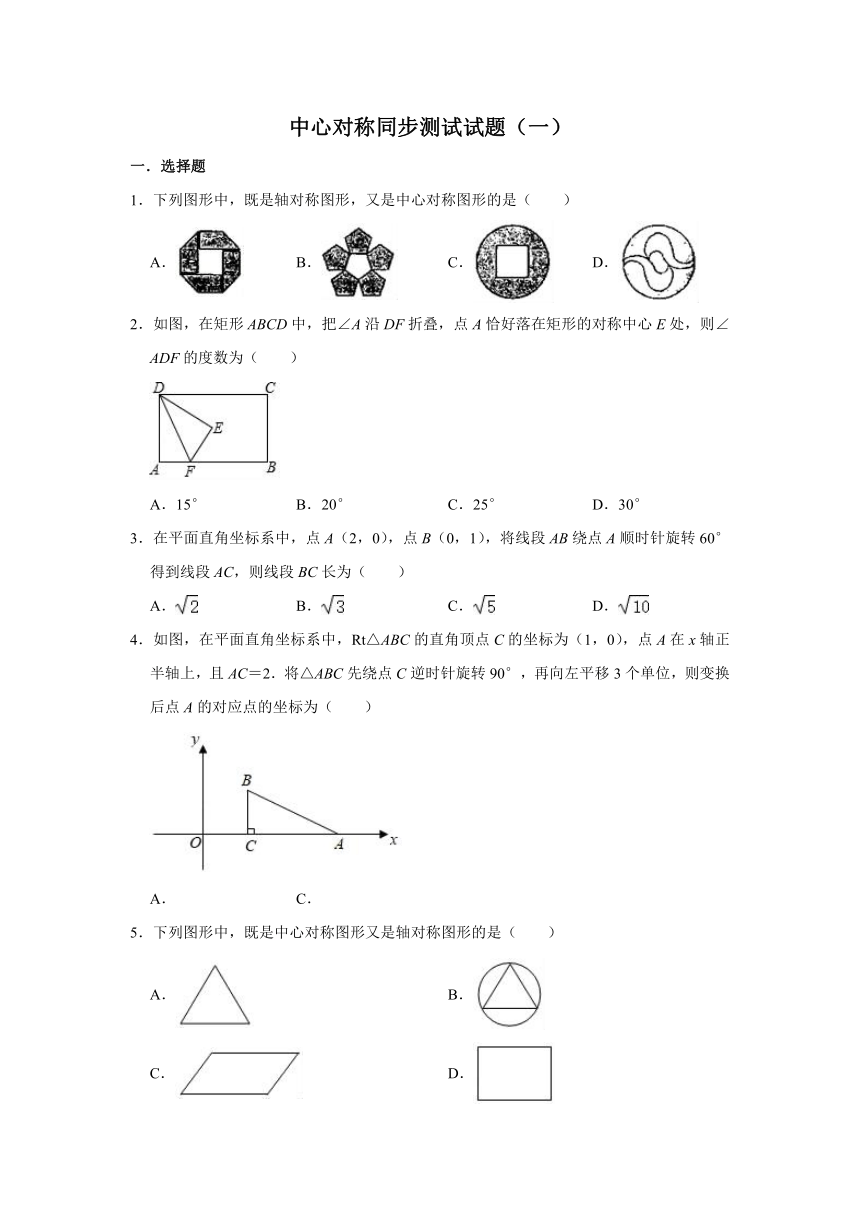
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,则∠ADF的度数为( )
A.15° B.20° C.25° D.30°
3.在平面直角坐标系中,点A(2,0),点B(0,1),将线段AB绕点A顺时针旋转60°得到线段AC,则线段BC长为( )
A. B. C. D.
4.如图,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为( )
A. C.
5.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
6.下面的图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
7.以下关于新型冠状病毒(2019﹣nCoV)的防范宣传图标中是中心对称图形的是( )
A. B.
C. D.
8.如图,指针OA,OB分别从与x轴和y轴重合的位置出发,绕着原点O顺时针转动,已知OA每秒转动45°,OB的转动速度是OA的,则第2020秒时,OA与OB之间夹角的度数为( )
A.130° B.145° C.150° D.165°
9.如图,在平面直角坐标系xOy中,△ABC与△A1B1C1是中心对称图形.则对称中心的坐标是( )
A. C.
10.下列图形中,中心对称图形个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.已知点A(a,﹣1)与点B(4,b)关于原点对称,则a+b= .
12.已知点A(a,3)与点B(2,﹣3)关于原点对称,则a= .
13.在平面直角坐标系中,将点P(﹣3,2)绕点Q(﹣1,0)顺时针旋转90°,所得到的对应点P′的坐标为 .
14.如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1,点A与A1是对应点,则点M的坐标是 .
15.如图,在直角坐标系中,已知点P0的坐标为(1,0),以O旋转中心,将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的倍,得到线段OP2;如此下去,得到线段OP3,OP4,…OPn(n为正整数),则点P2020的坐标是 .
三.解答题
16.如图,在平面直角坐标系中,点A(2,0),点B在第一象限,AB⊥OA,AB=OA,将△OAB绕点O按逆时针方向旋转105°得到△OA'B',连接BB'.
(Ⅰ)求∠OBB'的度数;
(Ⅱ)求出点B'的坐标.
17.如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?
18.如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,点B和点C重合.求证:四边形ACE′E是平行四边形.
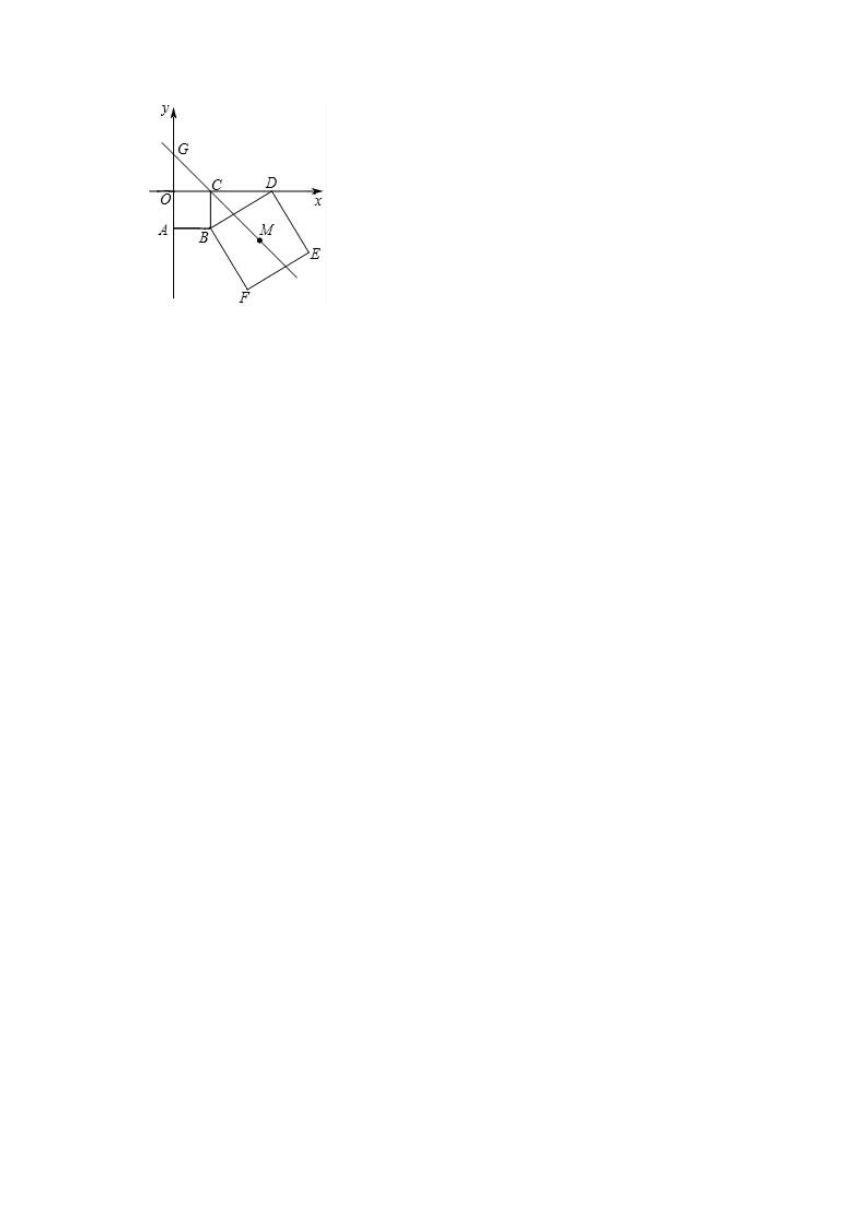
19.如图,正方形OABC的顶点B的坐标为(2,﹣2),D(m,0)为x轴上的一个动点(m>2),以BD为边作正方形BDEF,点E在第四象限.
(1)试判断线段AD与CF的数量关系,并说明理由;
(2)设正方形BDEF的对称中心为M,直线CM交y轴于点G.随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、是中心对称图形,不是轴对称图形,故本选项不符合题意;
B、不是中心对称图形,是轴对称图形,故本选项不符合题意;
C、既是中心对称图形又是轴对称图形,故本选项符合题意;
D、是中心对称图形,不是轴对称图形,故本选项不符合题意.
故选:C.
2.【解答】解:如图,连接AE,
∵把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,
∴AD=ED=AE,∠ADF=∠EDF=∠ADE,
∴△DAE是等边三角形,
∴∠ADE=60°,
∴∠ADF=30°,
故选:D.
3.【解答】解:如图,
∵A(2,0),B(0,1),
∴AB=AC==,
∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形,
∴BC=AB=
故选:C.
4.【解答】解:将△ABC先绕点C逆时针旋转90°,点A的对应点的坐标为(1,2),
再向左平移3个单位,变换后点A的对应点的坐标为(﹣2,2),
故选:D.
5.【解答】解:A.等边三角形是轴对称图形,不是中心对称图形,故本选项不合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.平行四边形是中心对称图形,不是轴对称图形,故本选项不合题意;
D.矩形既是中心对称图形又是轴对称图形,故本选项符合题意.
故选:D.
6.【解答】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项不合题意;
B、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项不合题意;
C、此图形旋转180°后不能与原图形重合,此图形不是中心对称图形,是轴对称图形,故此选项不合题意;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.
故选:D.
7.【解答】解:A、是中心对称图形,故此选项正确;
B、不是中心对称图形,故此选项错误;
C、不是中心对称图形,故此选项错误;
D、不是中心对称图形,故此选项错误;
故选:A.
8.【解答】解:设t秒第一次相遇.
由题意:270+15t=45t,
解得t=9,
相遇后设m秒第二次相遇,则有45t﹣15t=360,
解得t=12,
以后每过12秒相遇一次,
(2020﹣9)÷12=167…7,
∴2020秒时,7×45°﹣7×15°=210°,
此时OA与OB的夹角为150°
故选:C.
9.【解答】解:对称中心的坐标是(1,﹣1),
故选:C.
10.【解答】解:第一个图形是中心对称图形;
第二个图形是中心对称图形;
第三个图形是中心对称图形;
第四个图形不是中心对称图形;
共3个,
故选:C.
二.填空题(共5小题)
11.【解答】解:∵点A(a,﹣1)与点B(4,b)关于原点对称,
∴a=﹣4,b=1.
∴a+b=﹣4+1=﹣3,
故答案为:﹣3.
12.【解答】解:∵点A(a,3)与点B(2,﹣3)关于原点对称,
∴a=﹣2,
故答案为:﹣2.
13.【解答】解:如图,观察图象可知,P′(1,2).
故答案为(1,2).
14.【解答】解:如图,旋转中心M即为所求.M(1,﹣1).
故答案为(1,﹣1).
15.【解答】解:∵OP0=1,
∴P0的坐标为(1,0).
∴OP1=2.
∴P1的坐标为(,).
同理:OP2=4,
P2的坐标为(0,4).
OP3=8,
P3的坐标为(﹣4,4).
OP4=16,
P4的坐标为(﹣16,0).
OP5=25,
点P5的坐标为(﹣24,﹣24),
而2020=252×8+4,
所以点P2020的坐标在与点P4一样的x轴上,
而OP2020=22020,
所以点P2020的坐标为(﹣22020,0).
故答案为(﹣22020,0).
三.解答题(共4小题)
16.【解答】解:(Ⅰ)∵△OAB≌△OA′B′,
∴OB=OB′,
又∠BOB′=105°,
∴∠OBB′=∠OB′B=(180°﹣105°)=37.5°.
(Ⅱ)过点B′作B′C垂直于x轴,垂足为C.
∵OA=AB=2,∠OAB=90°,
∴∠AOB=45°,OB=OA=2,
∴∠COB′=180°﹣105°﹣45°=30°,
在Rt△OCB′中,B′C=OB′=,
∴OC=CB′=,
∴B′(﹣,).
17.【解答】解:∠B与∠F相等,理由如下:
∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,
∴∠B=∠DEC,
∵AF∥BE,
∴∠F=∠DEC,
∴∠B=∠F.
18.【解答】证明:∵DE是△ABC的中位线,
∴DE∥AC,DE=AC,
∵将△BDE绕着CB的中点D逆时针旋转180°,
点E到了点E′位置,
∴DE=DE′,
∴EE′=2DE=AC,
∴四边形ACE'E是平行四边形.
19.【解答】解:(1)结论:AD=CF.
理由:连接AD,CF.
∵四边形ABCO和四边形BDEF都是正方形,
∴AB=BC,BD=BF,∠ABC=∠FBD=90°,
∴∠ABD=∠FBD,
∴△ABD≌△CBF(SAS),
∴AD=CF.
(2)结论:点G的位置不发生变化.
理由:过点F作FH⊥CB交CB的延长线于点H.
∵∠BCD=∠DBF=∠H=90°,
∴∠CBD+∠FBH=90°,∠FBH+∠BFH=90°,
∴∠CBD=∠BFH,
∵BD=BF,
∴△BCD≌△FHB(AAS),
∴CD=BH=m﹣2,BC=FH=2,
∴F(4,﹣m),
又D(m,0),
∴M(2+,﹣),
作MN⊥x轴,在△CMN中,MN=,CN=,
∴△AMN是等腰直角三角形
一.选择题
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,则∠ADF的度数为( )
A.15° B.20° C.25° D.30°
3.在平面直角坐标系中,点A(2,0),点B(0,1),将线段AB绕点A顺时针旋转60°得到线段AC,则线段BC长为( )
A. B. C. D.
4.如图,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为( )
A. C.
5.下列图形中,既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
6.下面的图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
7.以下关于新型冠状病毒(2019﹣nCoV)的防范宣传图标中是中心对称图形的是( )
A. B.
C. D.
8.如图,指针OA,OB分别从与x轴和y轴重合的位置出发,绕着原点O顺时针转动,已知OA每秒转动45°,OB的转动速度是OA的,则第2020秒时,OA与OB之间夹角的度数为( )
A.130° B.145° C.150° D.165°
9.如图,在平面直角坐标系xOy中,△ABC与△A1B1C1是中心对称图形.则对称中心的坐标是( )
A. C.
10.下列图形中,中心对称图形个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题
11.已知点A(a,﹣1)与点B(4,b)关于原点对称,则a+b= .
12.已知点A(a,3)与点B(2,﹣3)关于原点对称,则a= .
13.在平面直角坐标系中,将点P(﹣3,2)绕点Q(﹣1,0)顺时针旋转90°,所得到的对应点P′的坐标为 .
14.如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1,点A与A1是对应点,则点M的坐标是 .
15.如图,在直角坐标系中,已知点P0的坐标为(1,0),以O旋转中心,将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的倍,得到线段OP2;如此下去,得到线段OP3,OP4,…OPn(n为正整数),则点P2020的坐标是 .
三.解答题
16.如图,在平面直角坐标系中,点A(2,0),点B在第一象限,AB⊥OA,AB=OA,将△OAB绕点O按逆时针方向旋转105°得到△OA'B',连接BB'.
(Ⅰ)求∠OBB'的度数;
(Ⅱ)求出点B'的坐标.
17.如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?
18.如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置,点B和点C重合.求证:四边形ACE′E是平行四边形.
19.如图,正方形OABC的顶点B的坐标为(2,﹣2),D(m,0)为x轴上的一个动点(m>2),以BD为边作正方形BDEF,点E在第四象限.
(1)试判断线段AD与CF的数量关系,并说明理由;
(2)设正方形BDEF的对称中心为M,直线CM交y轴于点G.随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:A、是中心对称图形,不是轴对称图形,故本选项不符合题意;
B、不是中心对称图形,是轴对称图形,故本选项不符合题意;
C、既是中心对称图形又是轴对称图形,故本选项符合题意;
D、是中心对称图形,不是轴对称图形,故本选项不符合题意.
故选:C.
2.【解答】解:如图,连接AE,
∵把∠A沿DF折叠,点A恰好落在矩形的对称中心E处,
∴AD=ED=AE,∠ADF=∠EDF=∠ADE,
∴△DAE是等边三角形,
∴∠ADE=60°,
∴∠ADF=30°,
故选:D.
3.【解答】解:如图,
∵A(2,0),B(0,1),
∴AB=AC==,
∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形,
∴BC=AB=
故选:C.
4.【解答】解:将△ABC先绕点C逆时针旋转90°,点A的对应点的坐标为(1,2),
再向左平移3个单位,变换后点A的对应点的坐标为(﹣2,2),
故选:D.
5.【解答】解:A.等边三角形是轴对称图形,不是中心对称图形,故本选项不合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.平行四边形是中心对称图形,不是轴对称图形,故本选项不合题意;
D.矩形既是中心对称图形又是轴对称图形,故本选项符合题意.
故选:D.
6.【解答】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项不合题意;
B、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,不是轴对称图形,故此选项不合题意;
C、此图形旋转180°后不能与原图形重合,此图形不是中心对称图形,是轴对称图形,故此选项不合题意;
D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确.
故选:D.
7.【解答】解:A、是中心对称图形,故此选项正确;
B、不是中心对称图形,故此选项错误;
C、不是中心对称图形,故此选项错误;
D、不是中心对称图形,故此选项错误;
故选:A.
8.【解答】解:设t秒第一次相遇.
由题意:270+15t=45t,
解得t=9,
相遇后设m秒第二次相遇,则有45t﹣15t=360,
解得t=12,
以后每过12秒相遇一次,
(2020﹣9)÷12=167…7,
∴2020秒时,7×45°﹣7×15°=210°,
此时OA与OB的夹角为150°
故选:C.
9.【解答】解:对称中心的坐标是(1,﹣1),
故选:C.
10.【解答】解:第一个图形是中心对称图形;
第二个图形是中心对称图形;
第三个图形是中心对称图形;
第四个图形不是中心对称图形;
共3个,
故选:C.
二.填空题(共5小题)
11.【解答】解:∵点A(a,﹣1)与点B(4,b)关于原点对称,
∴a=﹣4,b=1.
∴a+b=﹣4+1=﹣3,
故答案为:﹣3.
12.【解答】解:∵点A(a,3)与点B(2,﹣3)关于原点对称,
∴a=﹣2,
故答案为:﹣2.
13.【解答】解:如图,观察图象可知,P′(1,2).
故答案为(1,2).
14.【解答】解:如图,旋转中心M即为所求.M(1,﹣1).
故答案为(1,﹣1).
15.【解答】解:∵OP0=1,
∴P0的坐标为(1,0).
∴OP1=2.
∴P1的坐标为(,).
同理:OP2=4,
P2的坐标为(0,4).
OP3=8,
P3的坐标为(﹣4,4).
OP4=16,
P4的坐标为(﹣16,0).
OP5=25,
点P5的坐标为(﹣24,﹣24),
而2020=252×8+4,
所以点P2020的坐标在与点P4一样的x轴上,
而OP2020=22020,
所以点P2020的坐标为(﹣22020,0).
故答案为(﹣22020,0).
三.解答题(共4小题)
16.【解答】解:(Ⅰ)∵△OAB≌△OA′B′,
∴OB=OB′,
又∠BOB′=105°,
∴∠OBB′=∠OB′B=(180°﹣105°)=37.5°.
(Ⅱ)过点B′作B′C垂直于x轴,垂足为C.
∵OA=AB=2,∠OAB=90°,
∴∠AOB=45°,OB=OA=2,
∴∠COB′=180°﹣105°﹣45°=30°,
在Rt△OCB′中,B′C=OB′=,
∴OC=CB′=,
∴B′(﹣,).
17.【解答】解:∠B与∠F相等,理由如下:
∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,
∴∠B=∠DEC,
∵AF∥BE,
∴∠F=∠DEC,
∴∠B=∠F.
18.【解答】证明:∵DE是△ABC的中位线,
∴DE∥AC,DE=AC,
∵将△BDE绕着CB的中点D逆时针旋转180°,
点E到了点E′位置,
∴DE=DE′,
∴EE′=2DE=AC,
∴四边形ACE'E是平行四边形.
19.【解答】解:(1)结论:AD=CF.
理由:连接AD,CF.
∵四边形ABCO和四边形BDEF都是正方形,
∴AB=BC,BD=BF,∠ABC=∠FBD=90°,
∴∠ABD=∠FBD,
∴△ABD≌△CBF(SAS),
∴AD=CF.
(2)结论:点G的位置不发生变化.
理由:过点F作FH⊥CB交CB的延长线于点H.
∵∠BCD=∠DBF=∠H=90°,
∴∠CBD+∠FBH=90°,∠FBH+∠BFH=90°,
∴∠CBD=∠BFH,
∵BD=BF,
∴△BCD≌△FHB(AAS),
∴CD=BH=m﹣2,BC=FH=2,
∴F(4,﹣m),
又D(m,0),
∴M(2+,﹣),
作MN⊥x轴,在△CMN中,MN=,CN=,
∴△AMN是等腰直角三角形
同课章节目录
