人教版数学九年级上册 第24章 24.1圆的有关性质同步测试试题(一)(word解析版)
文档属性
| 名称 | 人教版数学九年级上册 第24章 24.1圆的有关性质同步测试试题(一)(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 366.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 00:00:00 | ||
图片预览


文档简介
圆的有关性质同步测试试题(一)
一.选择题
1.如图,点A、B、C在⊙O上,点D是AB延长线上一点,若∠CBD=55°,则∠AOC的度数为( )
A.100° B.105° C.125° D.110°
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=6,CD=4,则AE的长为( )
A. B. C. D.
3.如图,AB是⊙O的直径,BC是弦,点P是(含端点)上任意一点,若AB=13,BC=12,则AP的长不可能是( )
A.4 B.5 C.12 D.13
4.如图,AB是⊙O的直径,点C,D在⊙O上.若∠ABD=40°,则∠BCD的度数为( )
A.30° B.40° C.50° D.60°
5.如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是( )
A.2 B.4 C.6 D.8
6.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,下列说法正确的是( )
①若∠AOB=∠COD,则CD=AB;②若CD=AB,则CD,AB所对的弧相等;③若CD=AB,则点O到CD,AB的距离相等;④若∠AOB+∠COD=180°,且CD=6,则AB=8.
A.①②③④ B.①③④ C.①②④ D.③④
7.小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160mm,直角顶点到轮胎与底面接触点AB长为320mm,请帮小名计算轮胎的直径为( )mm.
A.350 B.700 C.800 D.400
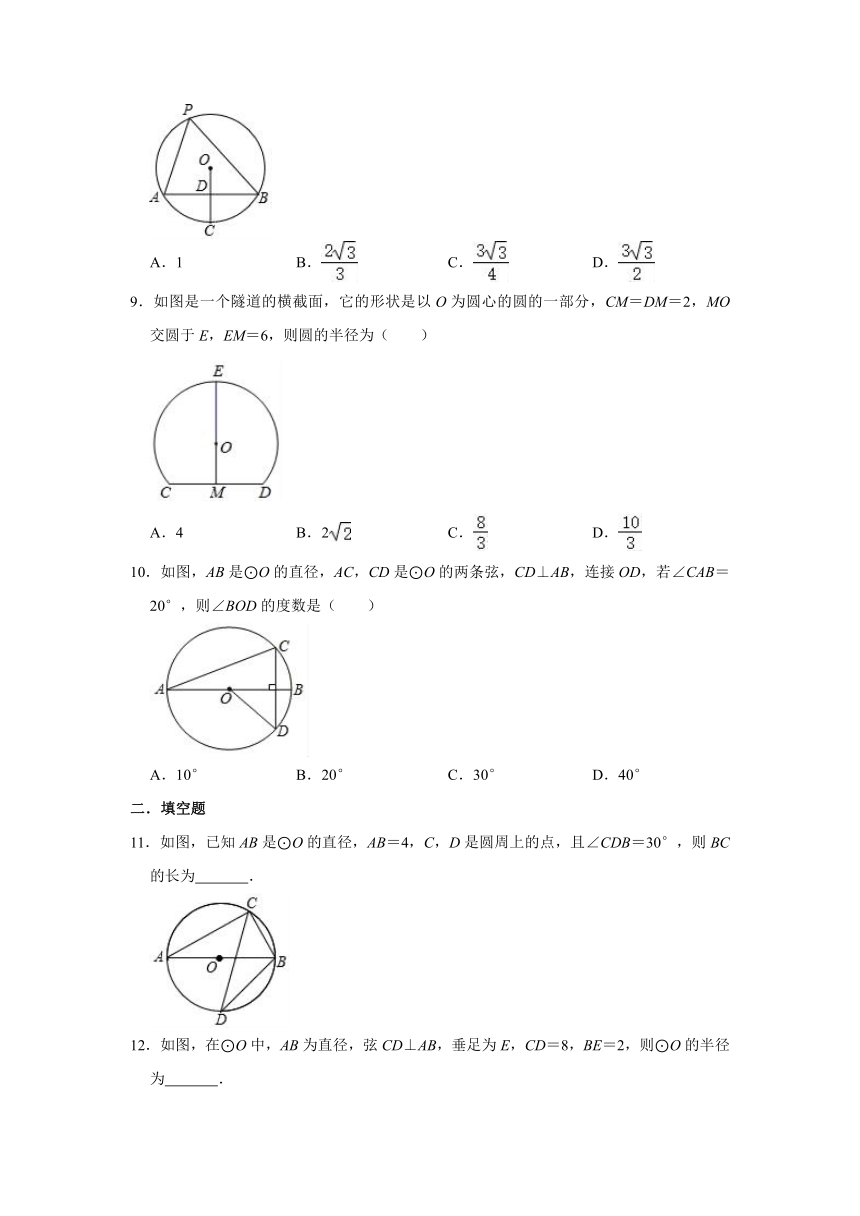
8.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则 S△PAB的最大值为( )
A.1 B. C. D.
9.如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,CM=DM=2,MO交圆于E,EM=6,则圆的半径为( )
A.4 B.2 C. D.
10.如图,AB是⊙O的直径,AC,CD是⊙O的两条弦,CD⊥AB,连接OD,若∠CAB=20°,则∠BOD的度数是( )
A.10° B.20° C.30° D.40°
二.填空题
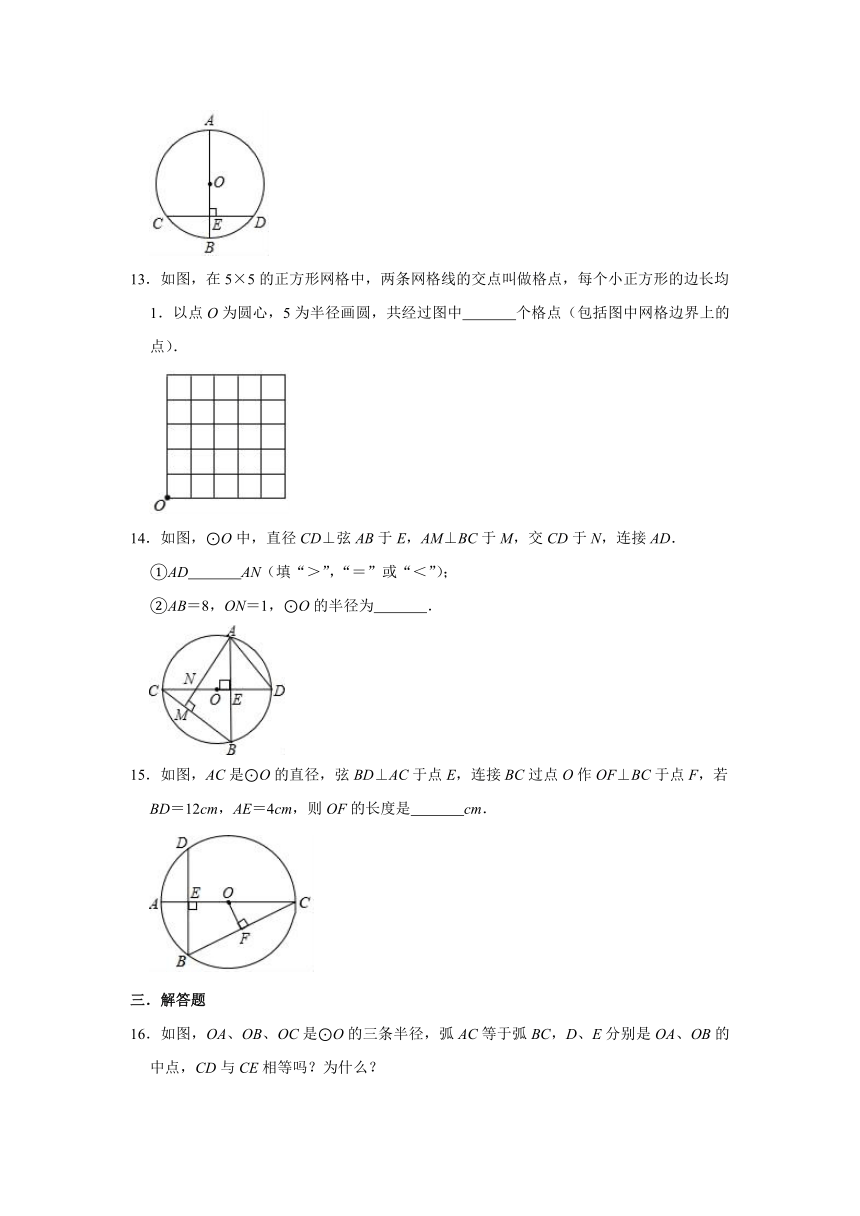
11.如图,已知AB是⊙O的直径,AB=4,C,D是圆周上的点,且∠CDB=30°,则BC的长为 .
12.如图,在⊙O中,AB为直径,弦CD⊥AB,垂足为E,CD=8,BE=2,则⊙O的半径为 .
13.如图,在5×5的正方形网格中,两条网格线的交点叫做格点,每个小正方形的边长均1.以点O为圆心,5为半径画圆,共经过图中 个格点(包括图中网格边界上的点).
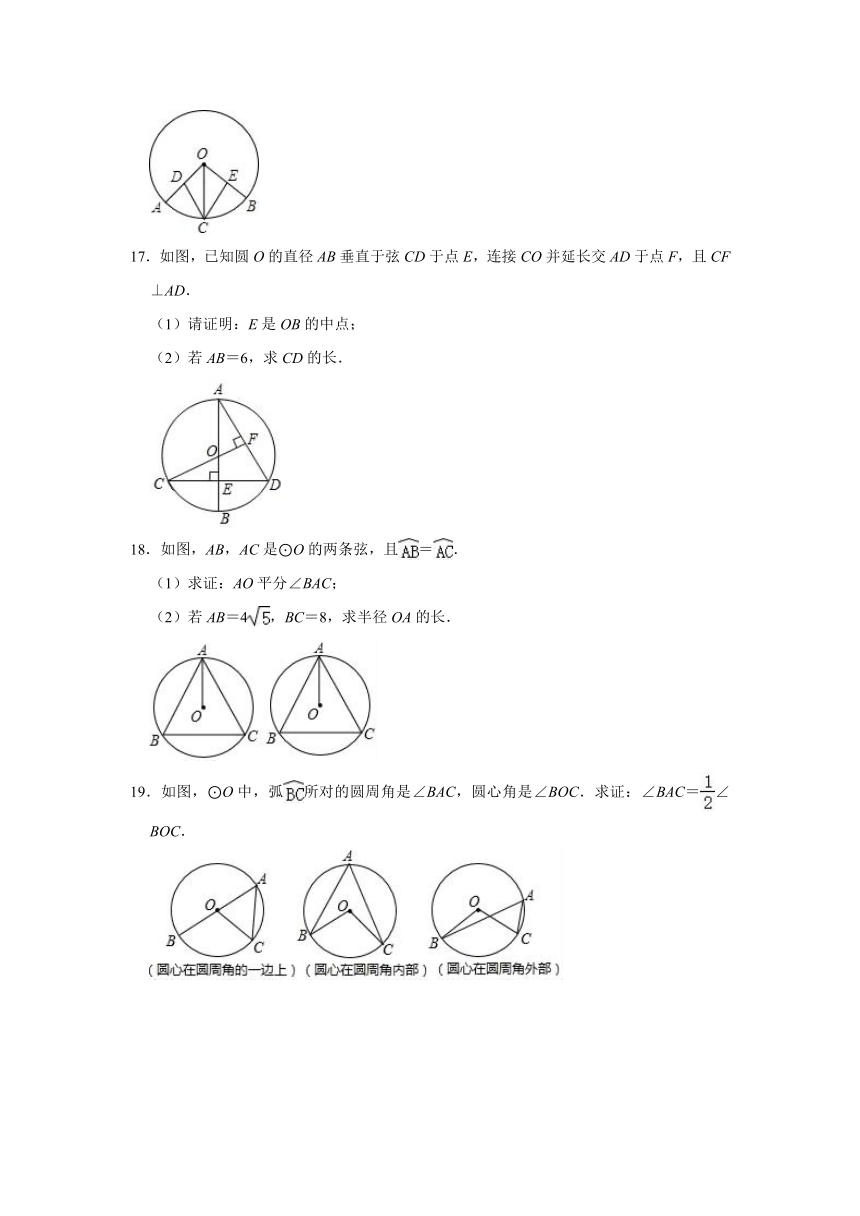
14.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
①AD AN(填“>”,“=”或“<”);
②AB=8,ON=1,⊙O的半径为 .
15.如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是 cm.
三.解答题
16.如图,OA、OB、OC是⊙O的三条半径,弧AC等于弧BC,D、E分别是OA、OB的中点,CD与CE相等吗?为什么?
17.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=6,求CD的长.
18.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
19.如图,⊙O中,弧所对的圆周角是∠BAC,圆心角是∠BOC.求证:∠BAC=∠BOC.
参考答案与试题解析
一.选择题
1.【解答】解:设点E是优弧AC(不与A,C重合)上的一点,连接AE、CE,如图所示:
∵∠CBD=55°.
∴∠E=∠CBD=55°.
∴∠AOC=2∠E=110°.
故选:D.
2.【解答】解:连接OC,如图,
∵CD⊥AB,
∴CE=DE=CD=2,
在Rt△OCE中,∵OC=3,CE=2,
∴OE==,
∴AE=OA+OE=3+.
故选:B.
3.【解答】解:连接AC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC===5,
∵点P是劣弧(含端点)上任意一点,
∴AC≤AP≤AB,
即5≤AP≤13.
故选:A.
4.【解答】解:由圆周角定理得,∠ACD=∠ABD=40°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCD=90°﹣40°=50°,
故选:C.
5.【解答】解:作OH⊥AB于H,连接OA、OD,如图,
∴AH=BH=AB=×8=4,
∵CD⊥OC,
∴CD=,
而OD为定值,OC最小时,CD最大,
∴当OC=OH时,CD的值最大,
∴CD的最大值为4.
故选:B.
6.【解答】解:因为在同圆中,若圆心角相等,则圆心角对的弦也相等;
若弦相等,那么该弦上的弦心距也相等.
所以①③正确;
因为在同圆中,若弦相等,则弦所对的劣弧和优弧也分别相等;
②中没有明确对应,所以不正确;
过O作OE⊥CD,OF⊥AB,垂足分别是点E、F.
∵OE⊥CD,CD=6,
∴∠1=∠COD,CE=3.
又∵OC=OB=5,
∴OE=4.
∵OF⊥AB,
∴∠2=∠AOB.
∵∠AOB+∠COD=180°,
∴∠1+∠2=90°.
∵∠1+∠C=90°,
∴∠2=∠C.
在△OEC与△OFB中,
∴△OEC≌△OFB(AAS).
∴BF=OE=4.
∴AB=8.故④正确.
故选:B.
7.【解答】解:如图,连接OB,OC,作CD⊥OB于D.
设⊙O半径为xmm,在Rt△OCD中,
由勾股定理得方程,(x﹣160)2+3202=x2,
解得,x=400,
∴2x=800,
答:车轱辘的直径为800mm.
故选:C.
8.【解答】解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为===.
故选:C.
9.【解答】解:连接OC,
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
设圆的半径是x,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
所以圆的半径长是.
故选:D.
10.【解答】解:连接AD,如图所示:
∵AB是⊙O的直径,CD⊥AB,
∴,
∴∠BAD=∠BAC=20°.
∴∠BOD=2∠BAD=40°,
故选:D.
二.填空题(共5小题)
11.【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠CDB=30°,AB=4,
∴BC=AB=2,
故答案为:2.
12.【解答】解:连接OC,如图所示:
∵CD⊥AB,
∴CE=DE=CD=4,
设⊙O的半径为r,则OE=r﹣2,OC=r,
在Rt△OCE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径为5.
故答案为:5.
13.【解答】解:如图,⊙O共经过图中 4个格点
故答案为4.
14.【解答】解:(1)AD=AN,
证明:∵CD⊥AB
∴∠CEB=90°
∴∠C+∠B=90°,
同理∠C+∠CNM=90°
∴∠CNM=∠B
∵∠CNM=∠AND
∴∠AND=∠B,
∵∠D=∠B,
∴∠AND=∠D,
∴AN=AD,
故答案为=;
(2)设OE的长为x,连接OA
∵AN=AD,CD⊥AB
∴DE=NE=x+1,
∴OD=OE+ED=x+x+1=2x+1,
∴OA=OD=2x+1,
∴在Rt△OAE中OE2+AE2=OA2,
∴x2+42=(2x+1)2.
解得x=或x=﹣3(不合题意,舍去),
∴OA=2x+1=2×+1=,
即⊙O的半径为,
故答案为.
15.【解答】解:连接OB,
∵AC是⊙O的直径,弦BD⊥AC,
∴BE=BD=6cm,
在Rt△OEB中,OB2=OE2+BE2,即OB2=(OB﹣4)2+62,
解得,OB=,
则EC=AC﹣AE=9,
BC===3,
∵OF⊥BC,
∴CF=BC=,
∴OF===(cm),
故答案为.
三.解答题(共4小题)
16.【解答】解:CD=CE,理由如下:
∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA=OB,D、E分别是OA、OB的中点,
∴OD=OE,
在△DOC和△EOC中,
,
∴△DOC≌△EOC(SAS),
∴CD=CE.
17.【解答】(1)证明:连接AC,如图所示:
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,
即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=6,
∴OC=AB=3,
又∵BE=OE,
∴OE=,
∴CE===,
∴CD=2CE=3.
18.【解答】证明:(1)连接OB、OC,
∵AB=AC,OC=OB,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
19.【解答】证明:当圆心O在∠BAC的一边上时.如图1中,
∵OA=OC,
∴∠A=∠ACO,
∵∠BOC=∠A+∠ACO,
∵∠BOC=2∠A,即∠BAC=∠BOC,
当圆心角在∠BAC内部时,如图2中,延长BO交⊙O于点D,连接CD,则
∠D=∠A(同弧或等弧所对的圆周角都相等),
∵OC=OD,
∴∠D=∠OCD,
∵∠BOC=∠D+∠OCD(三角形的一个外角等于与它不相等的两个内角的和)
一.选择题
1.如图,点A、B、C在⊙O上,点D是AB延长线上一点,若∠CBD=55°,则∠AOC的度数为( )
A.100° B.105° C.125° D.110°
2.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=6,CD=4,则AE的长为( )
A. B. C. D.
3.如图,AB是⊙O的直径,BC是弦,点P是(含端点)上任意一点,若AB=13,BC=12,则AP的长不可能是( )
A.4 B.5 C.12 D.13
4.如图,AB是⊙O的直径,点C,D在⊙O上.若∠ABD=40°,则∠BCD的度数为( )
A.30° B.40° C.50° D.60°
5.如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是( )
A.2 B.4 C.6 D.8
6.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,下列说法正确的是( )
①若∠AOB=∠COD,则CD=AB;②若CD=AB,则CD,AB所对的弧相等;③若CD=AB,则点O到CD,AB的距离相等;④若∠AOB+∠COD=180°,且CD=6,则AB=8.
A.①②③④ B.①③④ C.①②④ D.③④
7.小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160mm,直角顶点到轮胎与底面接触点AB长为320mm,请帮小名计算轮胎的直径为( )mm.
A.350 B.700 C.800 D.400
8.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则 S△PAB的最大值为( )
A.1 B. C. D.
9.如图是一个隧道的横截面,它的形状是以O为圆心的圆的一部分,CM=DM=2,MO交圆于E,EM=6,则圆的半径为( )
A.4 B.2 C. D.
10.如图,AB是⊙O的直径,AC,CD是⊙O的两条弦,CD⊥AB,连接OD,若∠CAB=20°,则∠BOD的度数是( )
A.10° B.20° C.30° D.40°
二.填空题
11.如图,已知AB是⊙O的直径,AB=4,C,D是圆周上的点,且∠CDB=30°,则BC的长为 .
12.如图,在⊙O中,AB为直径,弦CD⊥AB,垂足为E,CD=8,BE=2,则⊙O的半径为 .
13.如图,在5×5的正方形网格中,两条网格线的交点叫做格点,每个小正方形的边长均1.以点O为圆心,5为半径画圆,共经过图中 个格点(包括图中网格边界上的点).
14.如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
①AD AN(填“>”,“=”或“<”);
②AB=8,ON=1,⊙O的半径为 .
15.如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是 cm.
三.解答题
16.如图,OA、OB、OC是⊙O的三条半径,弧AC等于弧BC,D、E分别是OA、OB的中点,CD与CE相等吗?为什么?
17.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=6,求CD的长.
18.如图,AB,AC是⊙O的两条弦,且=.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
19.如图,⊙O中,弧所对的圆周角是∠BAC,圆心角是∠BOC.求证:∠BAC=∠BOC.
参考答案与试题解析
一.选择题
1.【解答】解:设点E是优弧AC(不与A,C重合)上的一点,连接AE、CE,如图所示:
∵∠CBD=55°.
∴∠E=∠CBD=55°.
∴∠AOC=2∠E=110°.
故选:D.
2.【解答】解:连接OC,如图,
∵CD⊥AB,
∴CE=DE=CD=2,
在Rt△OCE中,∵OC=3,CE=2,
∴OE==,
∴AE=OA+OE=3+.
故选:B.
3.【解答】解:连接AC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC===5,
∵点P是劣弧(含端点)上任意一点,
∴AC≤AP≤AB,
即5≤AP≤13.
故选:A.
4.【解答】解:由圆周角定理得,∠ACD=∠ABD=40°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCD=90°﹣40°=50°,
故选:C.
5.【解答】解:作OH⊥AB于H,连接OA、OD,如图,
∴AH=BH=AB=×8=4,
∵CD⊥OC,
∴CD=,
而OD为定值,OC最小时,CD最大,
∴当OC=OH时,CD的值最大,
∴CD的最大值为4.
故选:B.
6.【解答】解:因为在同圆中,若圆心角相等,则圆心角对的弦也相等;
若弦相等,那么该弦上的弦心距也相等.
所以①③正确;
因为在同圆中,若弦相等,则弦所对的劣弧和优弧也分别相等;
②中没有明确对应,所以不正确;
过O作OE⊥CD,OF⊥AB,垂足分别是点E、F.
∵OE⊥CD,CD=6,
∴∠1=∠COD,CE=3.
又∵OC=OB=5,
∴OE=4.
∵OF⊥AB,
∴∠2=∠AOB.
∵∠AOB+∠COD=180°,
∴∠1+∠2=90°.
∵∠1+∠C=90°,
∴∠2=∠C.
在△OEC与△OFB中,
∴△OEC≌△OFB(AAS).
∴BF=OE=4.
∴AB=8.故④正确.
故选:B.
7.【解答】解:如图,连接OB,OC,作CD⊥OB于D.
设⊙O半径为xmm,在Rt△OCD中,
由勾股定理得方程,(x﹣160)2+3202=x2,
解得,x=400,
∴2x=800,
答:车轱辘的直径为800mm.
故选:C.
8.【解答】解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为===.
故选:C.
9.【解答】解:连接OC,
∵M是⊙O弦CD的中点,
根据垂径定理:EM⊥CD,
设圆的半径是x,
在Rt△COM中,有OC2=CM2+OM2,
即:x2=22+(6﹣x)2,
解得:x=,
所以圆的半径长是.
故选:D.
10.【解答】解:连接AD,如图所示:
∵AB是⊙O的直径,CD⊥AB,
∴,
∴∠BAD=∠BAC=20°.
∴∠BOD=2∠BAD=40°,
故选:D.
二.填空题(共5小题)
11.【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠CDB=30°,AB=4,
∴BC=AB=2,
故答案为:2.
12.【解答】解:连接OC,如图所示:
∵CD⊥AB,
∴CE=DE=CD=4,
设⊙O的半径为r,则OE=r﹣2,OC=r,
在Rt△OCE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径为5.
故答案为:5.
13.【解答】解:如图,⊙O共经过图中 4个格点
故答案为4.
14.【解答】解:(1)AD=AN,
证明:∵CD⊥AB
∴∠CEB=90°
∴∠C+∠B=90°,
同理∠C+∠CNM=90°
∴∠CNM=∠B
∵∠CNM=∠AND
∴∠AND=∠B,
∵∠D=∠B,
∴∠AND=∠D,
∴AN=AD,
故答案为=;
(2)设OE的长为x,连接OA
∵AN=AD,CD⊥AB
∴DE=NE=x+1,
∴OD=OE+ED=x+x+1=2x+1,
∴OA=OD=2x+1,
∴在Rt△OAE中OE2+AE2=OA2,
∴x2+42=(2x+1)2.
解得x=或x=﹣3(不合题意,舍去),
∴OA=2x+1=2×+1=,
即⊙O的半径为,
故答案为.
15.【解答】解:连接OB,
∵AC是⊙O的直径,弦BD⊥AC,
∴BE=BD=6cm,
在Rt△OEB中,OB2=OE2+BE2,即OB2=(OB﹣4)2+62,
解得,OB=,
则EC=AC﹣AE=9,
BC===3,
∵OF⊥BC,
∴CF=BC=,
∴OF===(cm),
故答案为.
三.解答题(共4小题)
16.【解答】解:CD=CE,理由如下:
∵弧AC和弧BC相等,
∴∠AOC=∠BOC,
又∵OA=OB,D、E分别是OA、OB的中点,
∴OD=OE,
在△DOC和△EOC中,
,
∴△DOC≌△EOC(SAS),
∴CD=CE.
17.【解答】(1)证明:连接AC,如图所示:
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,
即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=6,
∴OC=AB=3,
又∵BE=OE,
∴OE=,
∴CE===,
∴CD=2CE=3.
18.【解答】证明:(1)连接OB、OC,
∵AB=AC,OC=OB,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
19.【解答】证明:当圆心O在∠BAC的一边上时.如图1中,
∵OA=OC,
∴∠A=∠ACO,
∵∠BOC=∠A+∠ACO,
∵∠BOC=2∠A,即∠BAC=∠BOC,
当圆心角在∠BAC内部时,如图2中,延长BO交⊙O于点D,连接CD,则
∠D=∠A(同弧或等弧所对的圆周角都相等),
∵OC=OD,
∴∠D=∠OCD,
∵∠BOC=∠D+∠OCD(三角形的一个外角等于与它不相等的两个内角的和)
同课章节目录
