鲁科版_必修2_ 第4章 匀速圆周运动 _ 第2节 向心力与向心加速度课件46张PPT
文档属性
| 名称 | 鲁科版_必修2_ 第4章 匀速圆周运动 _ 第2节 向心力与向心加速度课件46张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-28 19:49:10 | ||
图片预览




文档简介
复 习 提 问
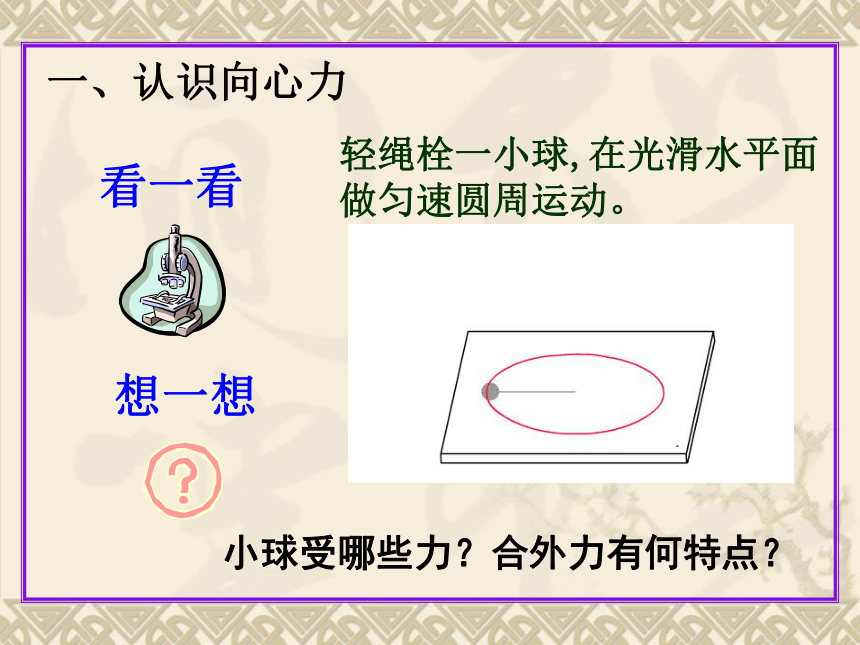
轻绳栓一小球,在光滑水平面
做匀速圆周运动。
分析向心来源的步骤:
1、找圆心
2、找轨道平面
3、找半径
4、受力分析
5、建坐标
6、力的分解、合成
7、求向心力
6、匀速圆周运动的条件
合外力刚好等于向心力
7、变速圆周运动的物体
合外力不会等于向心力
介绍: 向心力演示仪
介绍: 向心力演示仪
介绍: 向心力演示仪
介绍: 向心力演示仪
课 堂 小 结
一、向心力:
⑴ 大小:
⑵ 方向:沿半径指向圆心,是变力。
F⊥v,方向不断变化。
(3) 来源:重力、弹力、摩擦力或几个力的合力,或
某一个力的分力
练一练1: 画出下列物体所受的向心力
一个圆盘边缘系一根细绳,绳的下端拴着一个
质量为m的小球,圆盘的半径是r,绳子长为
L,圆盘匀速转动时小球随着一起转动,并且
细绳与竖直方向成θ角,如图所示,则圆盘转
动的角速度是多大。
如图所示,两个摩擦传动的轮子,A为主动
轮,转动的角速度为ω,已知A、B轮的半径
分别是R1和R2,C点离圆心的距离为R2/2,
求C点处的角速度和线速度。
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
通 用 技 术
§1.2 技术的性质
第2节 向心力与向心加速度
2、那么做圆周运动物体所受的外力有何特点?加速度又怎样呢?
1、如何确定物体的运动轨迹?
小球受哪些力?合外力有何特点?
想一想
看一看
一、认识向心力
G
FN
F
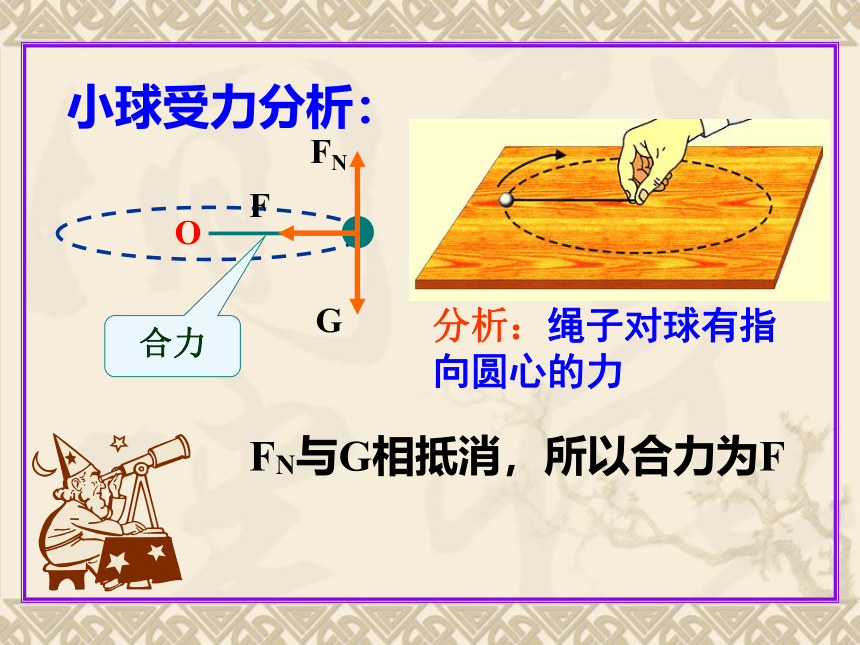
小球受力分析:
O
FN与G相抵消,所以合力为F
分析:绳子对球有指向圆心的力
合力
O
F
F
F
V
V
V
O
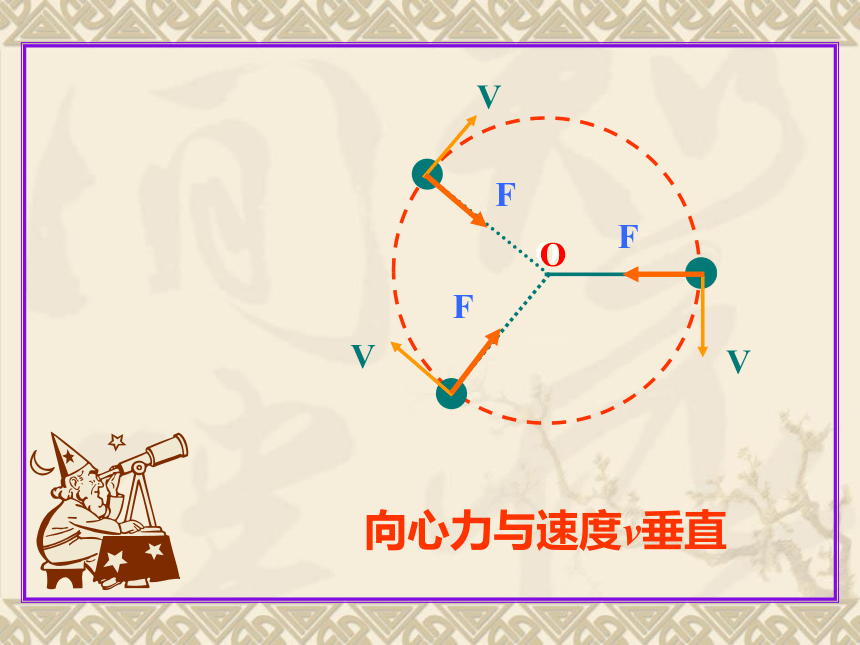
向心力与速度v垂直
2、向心力的方向:
沿半径指向圆心,即垂直于质点的运动方向
1、向心力定义:
做圆周运动的物体一定要所受到一个指向圆心的等效力,这个力叫向心力。
方向时刻发生变化,是变力。
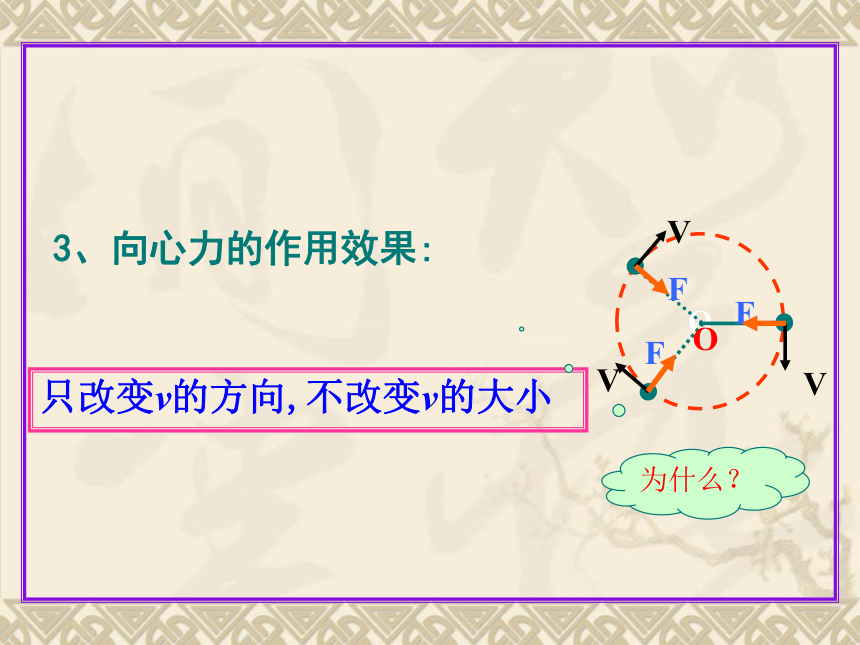
3、向心力的作用效果:
只改变v的方向,不改变v的大小
O
F
F
F
V
V
V
O
为什么?
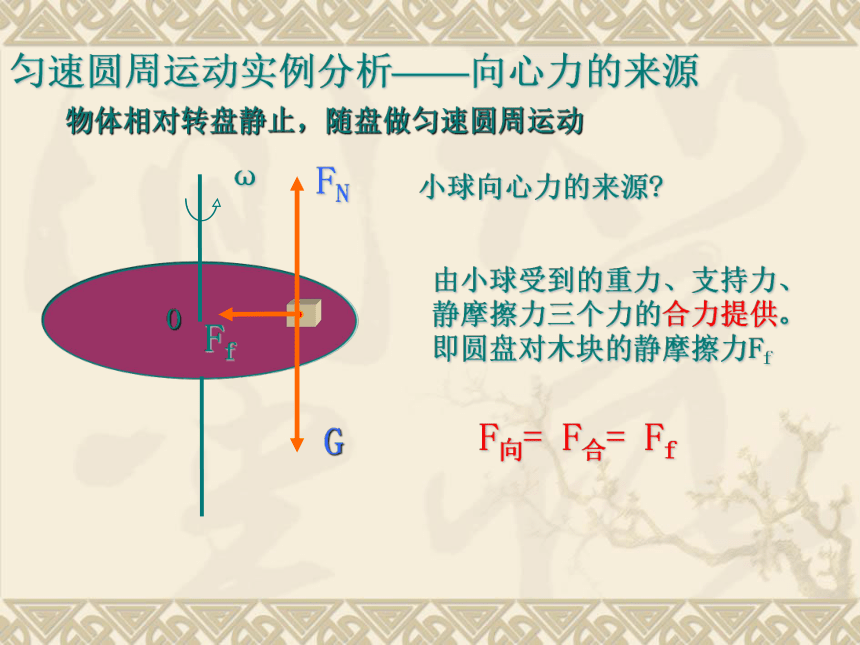
物体相对转盘静止,随盘做匀速圆周运动
F向= F合= Ff
由小球受到的重力、支持力、静摩擦力三个力的合力提供。
即圆盘对木块的静摩擦力Ff
ω
O
G
FN
Ff
小球向心力的来源?
匀速圆周运动实例分析——向心力的来源
G
Ff
FN
ω
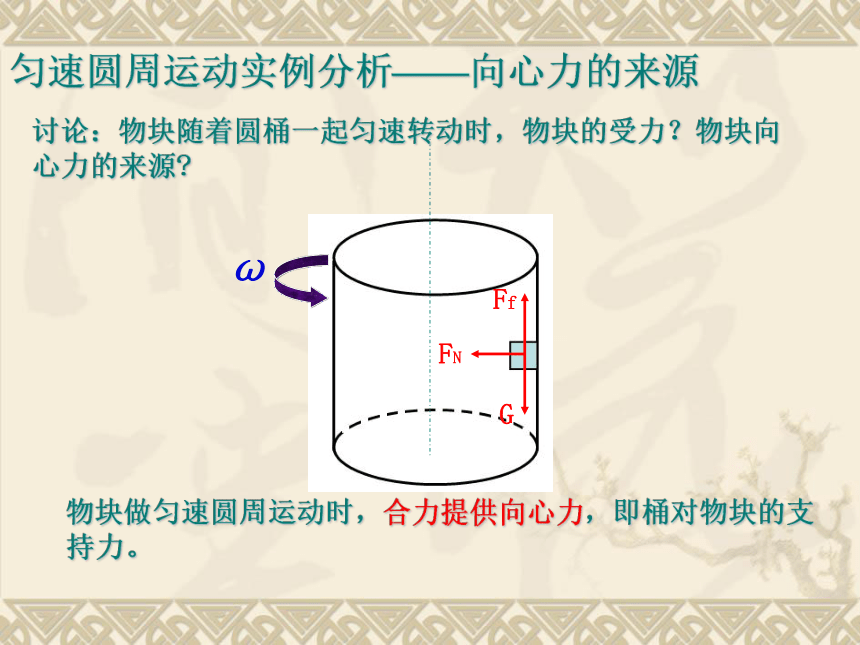
讨论:物块随着圆桶一起匀速转动时,物块的受力?物块向心力的来源?
物块做匀速圆周运动时,合力提供向心力,即桶对物块的支持力。
匀速圆周运动实例分析——向心力的来源
θ
O
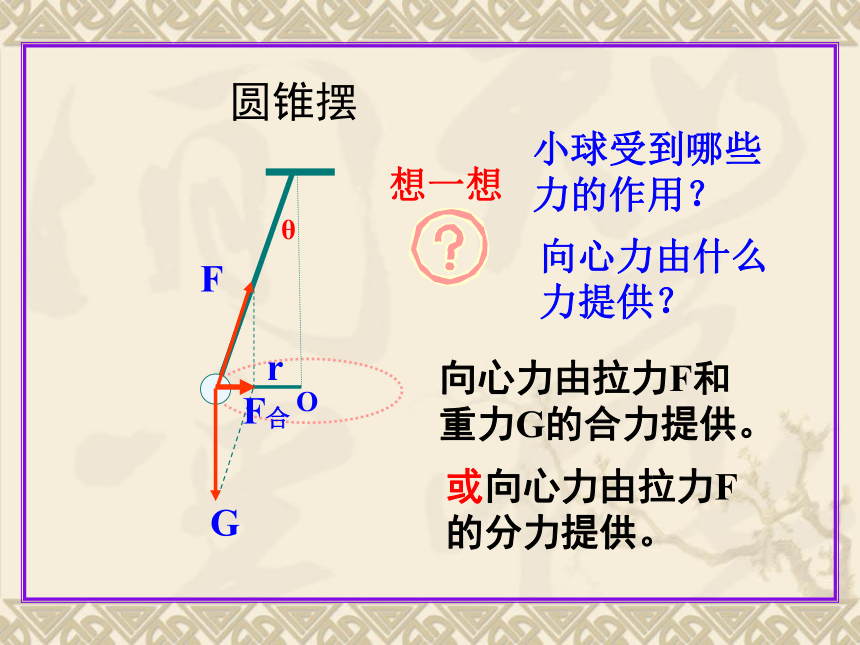
圆锥摆
G
F
F合
r
小球受到哪些力的作用?
向心力由拉力F和
重力G的合力提供。
向心力由什么力提供?
想一想
或向心力由拉力F的分力提供。
v
F
v
F
v
F
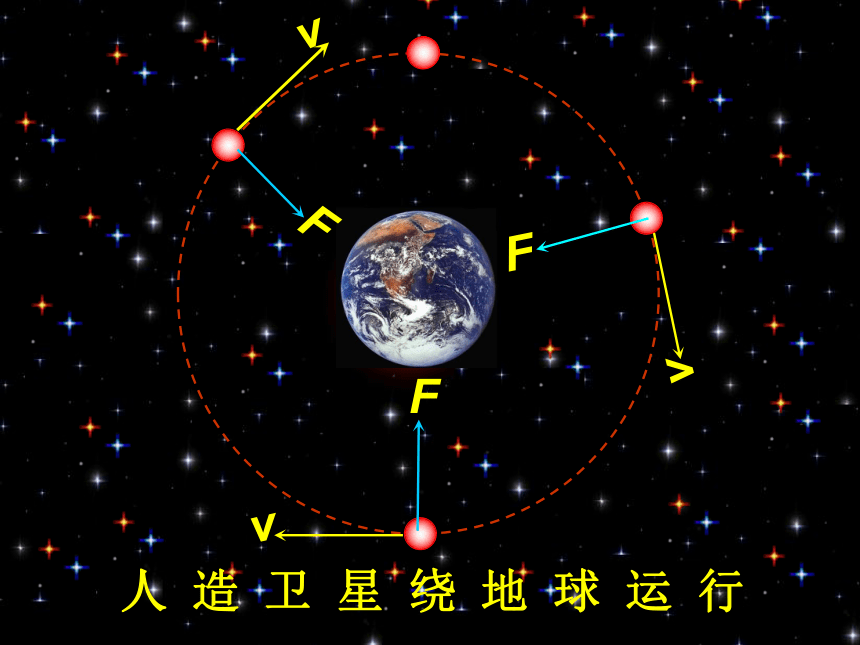
人 造 卫 星 绕 地 球 运 行
4、向心力的来源:
向心力可能是重力或弹力或摩擦力,或者是某个力的分力,还可能是它们的合力来提供。
向心力不是一种特殊性质的力,是根据力的效果来命名的,是一种效果力,也是一种等效力。
做变速圆周运动的物体所受的力
F
Fn
Ft
Ft 切向分力,改变速度的大小.
Fn 向心分力,改变速度的方向.
结论同时具有向心分力和切向分力的圆周运动就是变速圆周运动 ,匀速圆周运动切向分力为零。
加速
变速圆周
二、向心力大小
(1)体验向心力的大小
猜想:向心力大小可能与 _________________
______________________________ 有关
物体质量、
轨道半径、
运动快慢
(2)演示验:用向心力演示器演示(点击按钮演示)
方法:控制变量法
介绍: 向心力演示仪
G
FN
小
球
静
止
手
推
档
板
G
匀
速
圆
周
运
动
FN
F?
F
1.F与m的关系
保持r、ω一定
保持r、m一定
2.F与r的关系
保持m、ω一定
3.F与ω的关系
1、r、ω一定,F与m成正比
2、m、ω一定,F与r成正比
3、r、m一定,F与 ω2成正比
结论:向心力F的大小与物体质量m、圆周
半径r和角速度ω都有关系
说明:质量为m的质点,在半径为r的圆周上做匀速
圆周运动,线速度为v,角速度为ω,所需向
心力的大小为F
根据 推导向心力的另一表达式
(2)向心加速度作用效果?
向心加速度只改变线速度的方向
(3)怎样推导向心加速度的公式?
三、向心加速度
(1)向心加速度由谁产生?方向如何?
向心加速度是由向心力产生的,根据牛顿运动定律得到,这个加速度的方向与向心力的方向相同。
向心力公式: F向 = F合= mrω2
推导:
根据牛顿第二定律: F合= ma
或
a与r究竟是成正比呢,还是成反比?
想一想
若ω一定 , a与r就成正比 ;若v一定 , a与r就成反比 。
向心加速度的大小
(4)向心力和向心加速度公式的适用范围?
1、关于向心力说法中正确的是( )
A、物体由于做圆周运动而产生的力叫向心力;
B、向心力不改变速度的大小;
C、做匀速圆周运动的的物体所受向心力是不变的;
D、向心力是除物体所受重力、弹力以及摩擦力以外的一种新的力
B
练习
质量为m的球用长为L的细绳悬于天花板的O点,并使之在水平面内做匀速圆周运动,细线与竖直线成θ角,则以下正确的是( )
A.摆球受重力、拉力和向心力的作用
B.摆球只受重力、拉力的作用
C.摆球做匀速圆周运动的向心力
为mg? tgθ
D.摆球做匀速圆周运动的周期
为2π
Lcos
θ
√
g
B C D
练一练2
G
F
或:F=m
v2
r
F=mrω2
二、向心加速度:
⑴ 大小:a = rω2 或 a =
⑵ 方向:沿半径指向圆心,方向不断变化,
是变加速曲线运动。
v2
r
例题3:如图所示,两轮边缘挤压在一起,在两轮转动中,接触点不存在打滑的现象,A、B、C三点位置如图,r1=2r2,O1C=r2,则三点的向心加速度之比aA:aB:aC = _____ 。
B
A
C
r1
r2
O1
O2
2:4:1
质量为m的球用长为L的细绳悬于天花板的O点,并使之在水平面内做匀速圆周运动,细线与竖直线成θ角,则以下正确的是( )
A.摆球受重力、拉力和向心力的作用
B.摆球只受重力、拉力的作用
C.摆球做匀速圆周运动的向心力
为mg? tgθ
D.摆球做匀速圆周运动的周期
为2π
Lcos
θ
√
g
B C D
练一练2
G
F
F拉
G
F拉
G
N
f
G
N
N
G
G
N
F向= F拉
F向
F向= f
G
N
F向
F向
F向
例题1:小球做圆锥摆时细绳长L,与竖直方向成θ
角,求小球做匀速圆周运动的角速度ω。
O’
O
mg
T
F
小球受力:
竖直向下的重力G
沿绳方向的拉力T
小球的向心力:
由T和G的合力提供
解:
θ
L
小球做圆周运动的半径
由牛顿第二定律:
即:
R
受力分析时, 不能多出一个向心力。
练一练3
例题2:上海在北纬31°,求上海所在处物体绕地轴做圆周运动的向心加速度是多大?(设地球半径R=6400km,cos31°=0.86)
A
O
R
r
分析:首先应明确物体做匀速圆周运动;再确定
圆周轨迹、圆心及半径。
解:物体随地球自转的角速度
ω =2π/T
O’
圆周半径 r=R ? cos31°
∴ a=rω2
= R ? cos31°?(2π/T) 2
代入数据可得 a=2.9×10-2m/s2
例题3:如图所示,两轮边缘挤压在一起,在两轮转动中,接触点不存在打滑的现象,A、B、C三点位置如图,r1=2r2,O1C=r2,则三点的向心加速度之比aA:aB:aC = _____ 。
B
A
C
r1
r2
O1
O2
2:4:1
ωC= ωR1/R2
vC= ωR1/2
练一练4
例题4:飞机由俯冲转为拉起的一段轨迹可看作一段圆弧,如下图所示,飞机做俯冲拉起运动时,在最低点P附近作半径r =180m的圆周运动,如果飞行员的体重m =70kg,飞机经过最低点P时的速度v =360km/h,则这时飞行员对座位的压力为多大?(g=10m/s2)
P
r
v
4588.9N
如图所示,飞机在半径为R的竖直平面内翻斤斗,已知飞行员质量为m,飞机飞至最高点时,对座位压力为N,此时飞机的速度多大?
v
R
练一练5
θ
O
圆锥摆
G
F
F合
r
小球受到哪些力的作用?
向心力由拉力F和
重力G的合力提供。
向心力由什么力提供?
想一想
或向心力由拉力F的分力提供。
物体相对转盘静止,随盘做匀速圆周运动
F向=F合=Ff
木块做圆周运动所需向心力:
由圆盘对木块的静摩擦力f提供
ω
O
G
FN
Ff
小球受到哪些力的作用?
向心力由什么力提供?
想一想
2、用细线拴住一球做匀速圆周运动,下列说法中正确的是( )
A.在线速度一定情况下,线越长越易断
B.在线速度一定情况下,线越短越易断
C.在角速度一定情况下,线越长越易断
D.在角速度一定情况下,线越短越易断
BC
3、在光滑的横杆上穿着两质量不同的两个小球,小球用细线连接起来,当转台匀速转动时,下列说法正确的是( )
A.两小球速率必相等
B.两小球角速度必相等
C.两小球加速度必相等
D.两小球到转轴距离与其质量成反比
练习
BD
4、甲乙两物体都做匀速圆周运动,其质量之比为1∶2,转动半径之比为1∶2,在相同时间内甲转过4周,乙转过3周.则它们的向心力之比为( )
A.1∶4 B.2∶3
C.4∶9 D.9∶16
C
练习
θ
O'
O
R
ω
θ
ω
θ
m
m
O
r
mg
FN
F合
mg
FN
F合
F合=mg tanθ
竖直方向:FN cosθ=mg
水平方向:F合=mω2r
竖直方向:FN cosθ=mg
水平方向:F合=mω2 R sinθ
沿光滑漏斗或碗内壁做圆周运动的小球
轻绳栓一小球,在光滑水平面
做匀速圆周运动。
分析向心来源的步骤:
1、找圆心
2、找轨道平面
3、找半径
4、受力分析
5、建坐标
6、力的分解、合成
7、求向心力
6、匀速圆周运动的条件
合外力刚好等于向心力
7、变速圆周运动的物体
合外力不会等于向心力
介绍: 向心力演示仪
介绍: 向心力演示仪
介绍: 向心力演示仪
介绍: 向心力演示仪
课 堂 小 结
一、向心力:
⑴ 大小:
⑵ 方向:沿半径指向圆心,是变力。
F⊥v,方向不断变化。
(3) 来源:重力、弹力、摩擦力或几个力的合力,或
某一个力的分力
练一练1: 画出下列物体所受的向心力
一个圆盘边缘系一根细绳,绳的下端拴着一个
质量为m的小球,圆盘的半径是r,绳子长为
L,圆盘匀速转动时小球随着一起转动,并且
细绳与竖直方向成θ角,如图所示,则圆盘转
动的角速度是多大。
如图所示,两个摩擦传动的轮子,A为主动
轮,转动的角速度为ω,已知A、B轮的半径
分别是R1和R2,C点离圆心的距离为R2/2,
求C点处的角速度和线速度。
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
通 用 技 术
§1.2 技术的性质
第2节 向心力与向心加速度
2、那么做圆周运动物体所受的外力有何特点?加速度又怎样呢?
1、如何确定物体的运动轨迹?
小球受哪些力?合外力有何特点?
想一想
看一看
一、认识向心力
G
FN
F
小球受力分析:
O
FN与G相抵消,所以合力为F
分析:绳子对球有指向圆心的力
合力
O
F
F
F
V
V
V
O
向心力与速度v垂直
2、向心力的方向:
沿半径指向圆心,即垂直于质点的运动方向
1、向心力定义:
做圆周运动的物体一定要所受到一个指向圆心的等效力,这个力叫向心力。
方向时刻发生变化,是变力。
3、向心力的作用效果:
只改变v的方向,不改变v的大小
O
F
F
F
V
V
V
O
为什么?
物体相对转盘静止,随盘做匀速圆周运动
F向= F合= Ff
由小球受到的重力、支持力、静摩擦力三个力的合力提供。
即圆盘对木块的静摩擦力Ff
ω
O
G
FN
Ff
小球向心力的来源?
匀速圆周运动实例分析——向心力的来源
G
Ff
FN
ω
讨论:物块随着圆桶一起匀速转动时,物块的受力?物块向心力的来源?
物块做匀速圆周运动时,合力提供向心力,即桶对物块的支持力。
匀速圆周运动实例分析——向心力的来源
θ
O
圆锥摆
G
F
F合
r
小球受到哪些力的作用?
向心力由拉力F和
重力G的合力提供。
向心力由什么力提供?
想一想
或向心力由拉力F的分力提供。
v
F
v
F
v
F
人 造 卫 星 绕 地 球 运 行
4、向心力的来源:
向心力可能是重力或弹力或摩擦力,或者是某个力的分力,还可能是它们的合力来提供。
向心力不是一种特殊性质的力,是根据力的效果来命名的,是一种效果力,也是一种等效力。
做变速圆周运动的物体所受的力
F
Fn
Ft
Ft 切向分力,改变速度的大小.
Fn 向心分力,改变速度的方向.
结论同时具有向心分力和切向分力的圆周运动就是变速圆周运动 ,匀速圆周运动切向分力为零。
加速
变速圆周
二、向心力大小
(1)体验向心力的大小
猜想:向心力大小可能与 _________________
______________________________ 有关
物体质量、
轨道半径、
运动快慢
(2)演示验:用向心力演示器演示(点击按钮演示)
方法:控制变量法
介绍: 向心力演示仪
G
FN
小
球
静
止
手
推
档
板
G
匀
速
圆
周
运
动
FN
F?
F
1.F与m的关系
保持r、ω一定
保持r、m一定
2.F与r的关系
保持m、ω一定
3.F与ω的关系
1、r、ω一定,F与m成正比
2、m、ω一定,F与r成正比
3、r、m一定,F与 ω2成正比
结论:向心力F的大小与物体质量m、圆周
半径r和角速度ω都有关系
说明:质量为m的质点,在半径为r的圆周上做匀速
圆周运动,线速度为v,角速度为ω,所需向
心力的大小为F
根据 推导向心力的另一表达式
(2)向心加速度作用效果?
向心加速度只改变线速度的方向
(3)怎样推导向心加速度的公式?
三、向心加速度
(1)向心加速度由谁产生?方向如何?
向心加速度是由向心力产生的,根据牛顿运动定律得到,这个加速度的方向与向心力的方向相同。
向心力公式: F向 = F合= mrω2
推导:
根据牛顿第二定律: F合= ma
或
a与r究竟是成正比呢,还是成反比?
想一想
若ω一定 , a与r就成正比 ;若v一定 , a与r就成反比 。
向心加速度的大小
(4)向心力和向心加速度公式的适用范围?
1、关于向心力说法中正确的是( )
A、物体由于做圆周运动而产生的力叫向心力;
B、向心力不改变速度的大小;
C、做匀速圆周运动的的物体所受向心力是不变的;
D、向心力是除物体所受重力、弹力以及摩擦力以外的一种新的力
B
练习
质量为m的球用长为L的细绳悬于天花板的O点,并使之在水平面内做匀速圆周运动,细线与竖直线成θ角,则以下正确的是( )
A.摆球受重力、拉力和向心力的作用
B.摆球只受重力、拉力的作用
C.摆球做匀速圆周运动的向心力
为mg? tgθ
D.摆球做匀速圆周运动的周期
为2π
Lcos
θ
√
g
B C D
练一练2
G
F
或:F=m
v2
r
F=mrω2
二、向心加速度:
⑴ 大小:a = rω2 或 a =
⑵ 方向:沿半径指向圆心,方向不断变化,
是变加速曲线运动。
v2
r
例题3:如图所示,两轮边缘挤压在一起,在两轮转动中,接触点不存在打滑的现象,A、B、C三点位置如图,r1=2r2,O1C=r2,则三点的向心加速度之比aA:aB:aC = _____ 。
B
A
C
r1
r2
O1
O2
2:4:1
质量为m的球用长为L的细绳悬于天花板的O点,并使之在水平面内做匀速圆周运动,细线与竖直线成θ角,则以下正确的是( )
A.摆球受重力、拉力和向心力的作用
B.摆球只受重力、拉力的作用
C.摆球做匀速圆周运动的向心力
为mg? tgθ
D.摆球做匀速圆周运动的周期
为2π
Lcos
θ
√
g
B C D
练一练2
G
F
F拉
G
F拉
G
N
f
G
N
N
G
G
N
F向= F拉
F向
F向= f
G
N
F向
F向
F向
例题1:小球做圆锥摆时细绳长L,与竖直方向成θ
角,求小球做匀速圆周运动的角速度ω。
O’
O
mg
T
F
小球受力:
竖直向下的重力G
沿绳方向的拉力T
小球的向心力:
由T和G的合力提供
解:
θ
L
小球做圆周运动的半径
由牛顿第二定律:
即:
R
受力分析时, 不能多出一个向心力。
练一练3
例题2:上海在北纬31°,求上海所在处物体绕地轴做圆周运动的向心加速度是多大?(设地球半径R=6400km,cos31°=0.86)
A
O
R
r
分析:首先应明确物体做匀速圆周运动;再确定
圆周轨迹、圆心及半径。
解:物体随地球自转的角速度
ω =2π/T
O’
圆周半径 r=R ? cos31°
∴ a=rω2
= R ? cos31°?(2π/T) 2
代入数据可得 a=2.9×10-2m/s2
例题3:如图所示,两轮边缘挤压在一起,在两轮转动中,接触点不存在打滑的现象,A、B、C三点位置如图,r1=2r2,O1C=r2,则三点的向心加速度之比aA:aB:aC = _____ 。
B
A
C
r1
r2
O1
O2
2:4:1
ωC= ωR1/R2
vC= ωR1/2
练一练4
例题4:飞机由俯冲转为拉起的一段轨迹可看作一段圆弧,如下图所示,飞机做俯冲拉起运动时,在最低点P附近作半径r =180m的圆周运动,如果飞行员的体重m =70kg,飞机经过最低点P时的速度v =360km/h,则这时飞行员对座位的压力为多大?(g=10m/s2)
P
r
v
4588.9N
如图所示,飞机在半径为R的竖直平面内翻斤斗,已知飞行员质量为m,飞机飞至最高点时,对座位压力为N,此时飞机的速度多大?
v
R
练一练5
θ
O
圆锥摆
G
F
F合
r
小球受到哪些力的作用?
向心力由拉力F和
重力G的合力提供。
向心力由什么力提供?
想一想
或向心力由拉力F的分力提供。
物体相对转盘静止,随盘做匀速圆周运动
F向=F合=Ff
木块做圆周运动所需向心力:
由圆盘对木块的静摩擦力f提供
ω
O
G
FN
Ff
小球受到哪些力的作用?
向心力由什么力提供?
想一想
2、用细线拴住一球做匀速圆周运动,下列说法中正确的是( )
A.在线速度一定情况下,线越长越易断
B.在线速度一定情况下,线越短越易断
C.在角速度一定情况下,线越长越易断
D.在角速度一定情况下,线越短越易断
BC
3、在光滑的横杆上穿着两质量不同的两个小球,小球用细线连接起来,当转台匀速转动时,下列说法正确的是( )
A.两小球速率必相等
B.两小球角速度必相等
C.两小球加速度必相等
D.两小球到转轴距离与其质量成反比
练习
BD
4、甲乙两物体都做匀速圆周运动,其质量之比为1∶2,转动半径之比为1∶2,在相同时间内甲转过4周,乙转过3周.则它们的向心力之比为( )
A.1∶4 B.2∶3
C.4∶9 D.9∶16
C
练习
θ
O'
O
R
ω
θ
ω
θ
m
m
O
r
mg
FN
F合
mg
FN
F合
F合=mg tanθ
竖直方向:FN cosθ=mg
水平方向:F合=mω2r
竖直方向:FN cosθ=mg
水平方向:F合=mω2 R sinθ
沿光滑漏斗或碗内壁做圆周运动的小球
同课章节目录
- 第1章 功和功率
- 导入 神奇的机械
- 第1节 机械功
- 第2节 功和能
- 第3节 功率
- 第4节 人与机械
- 第2章 能的转化与守恒
- 导入 从水车到核电站
- 第1节 动能的改变
- 第2节 势能的改变
- 第3节 能量守恒定律
- 第4节 能源与可持续发展
- 第3章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 竖直方向上的抛体运动
- 第3节 平抛运动
- 第4节 斜抛运动
- 第4章 匀速圆周运动
- 导入 身边的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 向心力与向心加速度
- 第3节 向心力的实例分析
- 第4节 离心运动
- 第5章 万有引力定律及其应用
- 导入 从嫦娥奔月到“阿波罗”上天
- 第1节 万有引力定律及引力常量的测定
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈追求
- 第6章 相对论与量子论初步
- 导入 迈入新世界
- 第1节 高速世界
- 第2节 量子世界
