空间向量法求二面角的计算(共27张PPT)
文档属性
| 名称 | 空间向量法求二面角的计算(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 08:29:28 | ||
图片预览







文档简介
(共27张PPT)
向量法求二面角的计算
湖南省衡阳市衡南县衡云中学
高中数学教师欧阳文丰
1、二面角的平面角
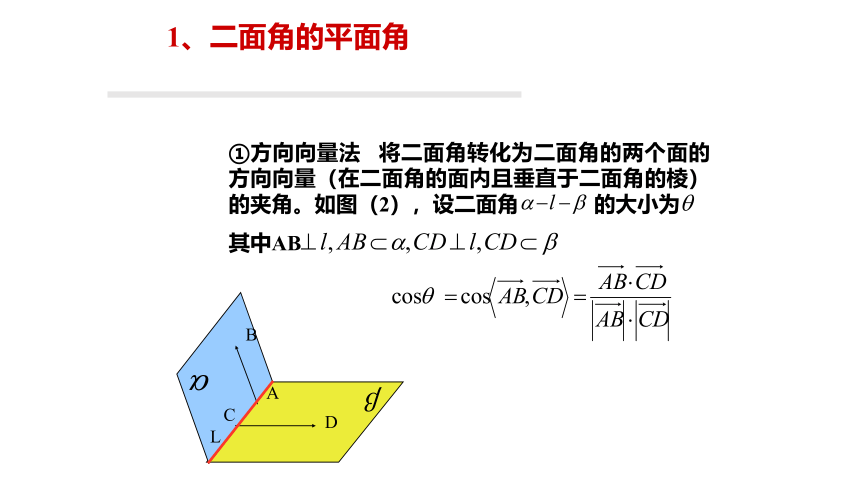
①方向向量法
将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角。如图(2),设二面角
的大小为
其中AB
D
C
L
B
A
注意法向量的方向:同进同出,二面角等于法向量夹角的补角;一进一出,二面角等于法向量夹角。
L
将二面角转化为二面角的两个面的法向量的夹角。如图,向量
,
则二面角
的大小
=〈
〉
2、二面角
若二面角
的大小为
,
则
②法向量法
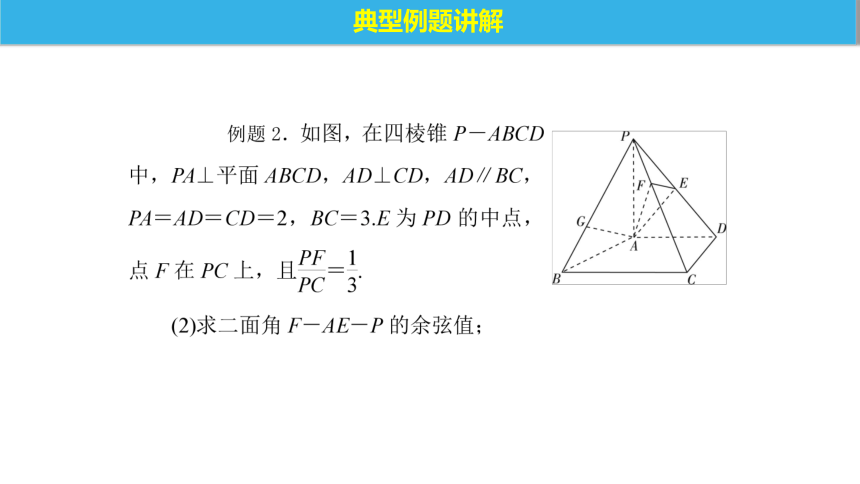
典型例题讲解
例1 在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,E是PD的中点,求平面EAC与平面ABCD的夹角.
解答
方法一 如图,以A为原点,分别以AC,AB,AP所在直线为x轴,y轴,z轴建立空间直角坐标系.
设PA=AB=a,AC=b,连接BD与AC交于点O,取AD中点F,
∴D(b,-a,0),P(0,0,a),
∴∠EOF等于平面EAC与平面ABCD的夹角(或补角).
∴平面EAC与平面ABCD的夹角为45°.
方法二 建系如方法一,
∵PA⊥平面ABCD,
设平面AEC的法向量为m=(x,y,z).
∴x=0,y=z.∴取m=(0,1,1),
∴平面AEC与平面ABCD的夹角为45°.
(二面角为法向量的夹角的等角。)
反思与感悟
(1)当空间直角坐标系容易建立(有特殊的位置关系)时,用向量法求解二面角无需作出二面角的平面角.只需求出平面的法向量,经过简单的运算即可求出,有时不易判断两法向量的夹角的大小就是二面角的大小(相等或互补),但我们可以根据图形观察得到结论,因为二面角是钝二面角还是锐二面角一般是明显的.
(2)注意法向量的方向:一进一出,二面角等于法向量夹角;同进同出,二面角等于法向量夹角的补角.
典型例题讲解
(二面角为法向量的夹角的补角。)
(注意:题目要求是求二面角的正弦值。)
4、在如图的实验装置中,正方形框架的边长都是1,且平面ABCD与平面ABEF互相垂直。活动弹子M,N分别在正方形对角线AC和BF上移动,且CM和BN的长度保持相等,记CM=BN=
(2)a
为何值时?MN的长最小?
(3)当MN的长最小时,求面MNA与面MNB所成二面角的余弦值。
A
B
C
D
E
F
M
N
跟踪训练1 若PA⊥平面ABC,AC⊥BC,PA=AC=1,BC=
,求二面角A-PB-C的余弦值.
课堂练面PAB的法向量为m=(x,y,z),
设平面PBC的法向量为n=(x′,y′,z′),
令y′=-1,则z′=-1,故n=(0,-1,-1),
又∵二面角A-PB-C是钝二面角,
(二面角为法向量的夹角的补角。)
跟踪训练2如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
PD.
求二面角Q-BP-C的余弦值.
答案:二面角Q-BP-C的余弦值为
.(二面角为法向量的夹角的等角。)
跟踪训练3如图所示,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
求二面角A1—BD—C1的余弦值.
答案:二面角A1-BD-C1的余弦值为
.
(二面角为法向量的夹角的补角。)
4、如图6,在棱长为
的正方体
中,
分别是棱AB,BC上的动点,且
。
(1)求证:
;
(2)当三棱锥
的体积取最大值时,求二面角
的正切值。
O’
C’
B’
A’
O
A
B
C
E
F
图6
O’
C’
B’
A’
O
A
B
C
E
F
图6
向量法求二面角的计算
湖南省衡阳市衡南县衡云中学
高中数学教师欧阳文丰
1、二面角的平面角
①方向向量法
将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角。如图(2),设二面角
的大小为
其中AB
D
C
L
B
A
注意法向量的方向:同进同出,二面角等于法向量夹角的补角;一进一出,二面角等于法向量夹角。
L
将二面角转化为二面角的两个面的法向量的夹角。如图,向量
,
则二面角
的大小
=〈
〉
2、二面角
若二面角
的大小为
,
则
②法向量法
典型例题讲解
例1 在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,E是PD的中点,求平面EAC与平面ABCD的夹角.
解答
方法一 如图,以A为原点,分别以AC,AB,AP所在直线为x轴,y轴,z轴建立空间直角坐标系.
设PA=AB=a,AC=b,连接BD与AC交于点O,取AD中点F,
∴D(b,-a,0),P(0,0,a),
∴∠EOF等于平面EAC与平面ABCD的夹角(或补角).
∴平面EAC与平面ABCD的夹角为45°.
方法二 建系如方法一,
∵PA⊥平面ABCD,
设平面AEC的法向量为m=(x,y,z).
∴x=0,y=z.∴取m=(0,1,1),
∴平面AEC与平面ABCD的夹角为45°.
(二面角为法向量的夹角的等角。)
反思与感悟
(1)当空间直角坐标系容易建立(有特殊的位置关系)时,用向量法求解二面角无需作出二面角的平面角.只需求出平面的法向量,经过简单的运算即可求出,有时不易判断两法向量的夹角的大小就是二面角的大小(相等或互补),但我们可以根据图形观察得到结论,因为二面角是钝二面角还是锐二面角一般是明显的.
(2)注意法向量的方向:一进一出,二面角等于法向量夹角;同进同出,二面角等于法向量夹角的补角.
典型例题讲解
(二面角为法向量的夹角的补角。)
(注意:题目要求是求二面角的正弦值。)
4、在如图的实验装置中,正方形框架的边长都是1,且平面ABCD与平面ABEF互相垂直。活动弹子M,N分别在正方形对角线AC和BF上移动,且CM和BN的长度保持相等,记CM=BN=
(2)a
为何值时?MN的长最小?
(3)当MN的长最小时,求面MNA与面MNB所成二面角的余弦值。
A
B
C
D
E
F
M
N
跟踪训练1 若PA⊥平面ABC,AC⊥BC,PA=AC=1,BC=
,求二面角A-PB-C的余弦值.
课堂练面PAB的法向量为m=(x,y,z),
设平面PBC的法向量为n=(x′,y′,z′),
令y′=-1,则z′=-1,故n=(0,-1,-1),
又∵二面角A-PB-C是钝二面角,
(二面角为法向量的夹角的补角。)
跟踪训练2如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=
PD.
求二面角Q-BP-C的余弦值.
答案:二面角Q-BP-C的余弦值为
.(二面角为法向量的夹角的等角。)
跟踪训练3如图所示,在直四棱柱ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.
求二面角A1—BD—C1的余弦值.
答案:二面角A1-BD-C1的余弦值为
.
(二面角为法向量的夹角的补角。)
4、如图6,在棱长为
的正方体
中,
分别是棱AB,BC上的动点,且
。
(1)求证:
;
(2)当三棱锥
的体积取最大值时,求二面角
的正切值。
O’
C’
B’
A’
O
A
B
C
E
F
图6
O’
C’
B’
A’
O
A
B
C
E
F
图6
