六年级下册数学课件-4.4正比例 人教版(共29张PPT)
文档属性
| 名称 | 六年级下册数学课件-4.4正比例 人教版(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 21.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 17:54:22 | ||
图片预览







文档简介
(共29张PPT)
第4课时
正比例
RJ
六年级下册
4
比例
已知路程和时间,怎样求速度?
速度
=
路程÷时间
已知总价和数量,怎样求单价?
单价
=
总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率
=
工作总量÷工作时间
探究点
1
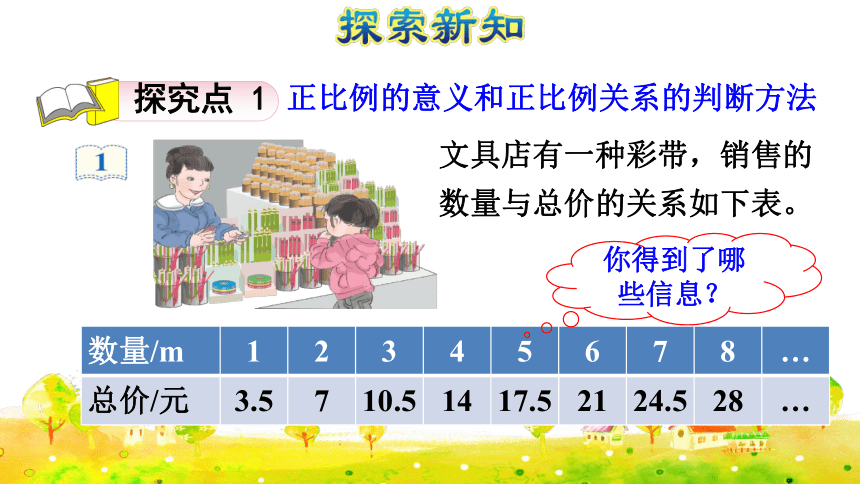
正比例的意义和正比例关系的判断方法
数量/m
1
2
3
4
5
6
7
8
…
总价/元
3.5
7
10.5
14
17.5
21
24.5
28
…
文具店有一种彩带,销售的数量与总价的关系如下表。
你得到了哪些信息?
数量/m
1
2
3
4
5
6
7
8
…
总价/元
3.5
7
10.5
14
17.5
21
24.5
28
…
说一说:表中有哪两种量?
数量和总价
总价和数量是两种相关联的量
数量增加,总价随着增加。
数量减少,总价随着减少。
从表中你还能知道什么?
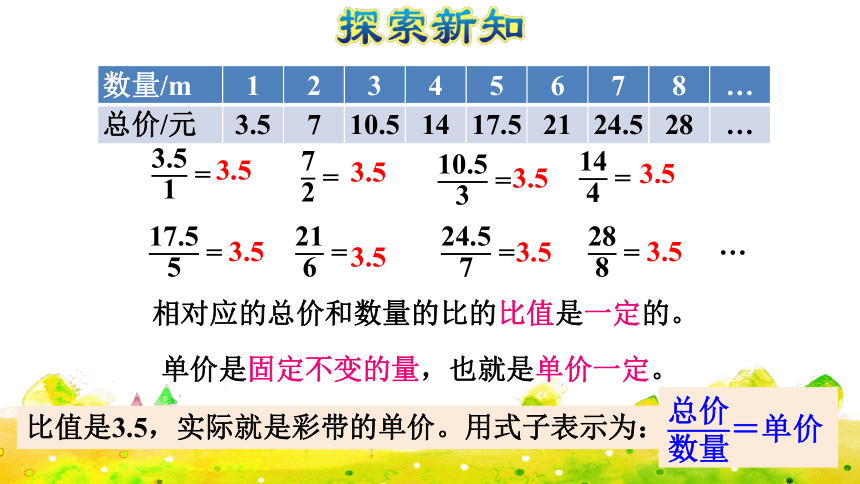
相对应的总价和数量的比的比值是一定的。
单价是固定不变的量,也就是单价一定。
比值是3.5,实际就是彩带的单价。用式子表示为:
=单价
数量/m
1
2
3
4
5
6
7
8
…
总价/元
3.5
7
10.5
14
17.5
21
24.5
28
…
3.5
3.5
3.5
3.5
3.5
3.5
3.5
3.5
…
=
=
=
=
=
=
=
=
数量/m
1
2
3
4
5
6
7
8
…
总价/元
3.5
7
10.5
14
17.5
21
24.5
28
…
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫正比例关系。
本题总价和数量是成正比例的量,总价与数量成正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
x
y
=
k(一定)
两种量成正比例关系要满足以下三个条件:
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的比值(也就是商)一定。
小试牛刀
n
0
1
2
3
4
5
6
…
2n
0
2
4
…
1.用n表示自然数,把下表填写完成。(选题源于教材P50第6题)
6
8
10
12
探究点
2
正比例图象的特点
根据图象回答下面的问题:
0
2
4
6
8
10
12
14
7
14
21
28
35
42
49
(1)从图中你发现了什么?
答:这个图象是一条逐渐上升的直的线。
总价/元
数量/m
总价/元
数量/m
0
2
4
6
8
10
12
14
7
14
21
28
35
42
49
答:这两个点也在这条射线上,并且射线又在上升,它们的单价相等。
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象连起来并延长,你还能发现什么?
总价/元
数量/m
0
2
4
6
8
10
12
14
7
14
21
28
35
42
49
(3)不计算,根据图象判断,如果买9
m彩带,总价是多少?49元能买多少米彩带?
答:通过观察,我发现买9
m彩带总价是31.5元,49元能买14
m彩带。
31.5
总价/元
数量/m
0
2
4
6
8
10
12
14
7
14
21
28
35
42
49
31.5
(4)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?
答:因为彩带的数量成倍地增加,总价也会成倍地增加,所以他花的钱是小丽的2倍。
彩带的单价一定
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
1.填空。
(1)为提高自身的阅读能力,学生们积极订阅书刊,认真阅读。某书店销售《小学生天地》的份数和总价如下表:
①表中( )和( )是相关联的量,( )增加,( )也随着增加。
份数
份数/份
1
2
3
4
5
6
…
总价/元
30
60
90
120
150
180
…
总价
份数
总价
②总价与份数这两个相关联的量中相对应的两个数的比值都是( ),这个比值实际上是( )。
③因为总价与份数的比值一定,所以表中的两种量叫做成( )的量。
(2)
路程与时间的比值是( ),当这个比值一定时,
( )和( )成( )比例关系。
正比例
速度
路程
时间
正
30
《小学生天地》的单价
2.判断。(对的画“√”,错的画“×”)
(1)长方形的长一定,宽和面积成正比例关系。
( )
(2)正方形的面积与边长成正比例关系。
( )
(3)比的前项一定,比的后项和比值成正比例关系。
( )
(4)x÷y=4,x和y成正比例关系。
( )
3.选择。(将正确答案的字母填在括号里)
(1)
下列各组中两种量不成正比例关系的是( )。
A.人的身高与年龄
B.y=5x,y和x
C.工作效率一定,工作总量和工作时间
D.圆的周长与直径
A
(2)
甲数的
与乙数的
相等(甲、乙均不为0),甲数与乙数(
)。
A.成正比例关系
B.不成正比例关系
C.无法判断
A
4.一辆汽车行驶的时间和路程如下表。
(选题源于教材P46做一做)
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
(1)写出几组路程与相对应的时间的比,并比较比值的大小。
80
∶1
160
∶2
240
∶3
320
∶4
400
∶5
480
∶6
比值相等(一定)。
(2)说一说这个比值表示什么。
这个比值表示速度。
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例关系。因为路程随着时间的变化而变化,而且
=速度(一定),所以成正比例关系。
路程
时间
(4)在图中描出表示路程和相对应时间的点,然后把它们按顺序连起来。并估计一下行驶120
km大约要用多少时间。
行驶120
km大约要用1.5时。
5.判断下面各题中的两种量是否成正比例关系,并说明理由。
(1)三角形的底一定,面积和高。
(2)成活率一定,栽树的棵数和成活的棵数。
(3)圆的面积和它的半径。
不成比例关系。
理由:
=π×半径
6.在梯形中,面积和哪种量成正比例关系?
如果梯形的高一定,那么面积与上下底的和成正比例关系;如果梯形的上下底的和一定,那么面积与高成正比例关系。
辨析:要正确理解正比例关系。
这节课你有哪些收获?
正比例:
1.
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
判断两个量是否成正比例关系的基本步骤:
首先判断两个量是不是相关联的量。
然后再看两个量的商是否为定值。
正比例图象的特点:
正比例关系的图象是一条直的线。从图象中可以直观地看到相对应两种量的变化情况。不用计算,由一种量的值可以直接找到相对应的另一种量的值。
作
业
请完成教材第49页练习九第1题、第2题、第3题、第4题、第5题。
thank
you!
第4课时
正比例
RJ
六年级下册
4
比例
已知路程和时间,怎样求速度?
速度
=
路程÷时间
已知总价和数量,怎样求单价?
单价
=
总价÷数量
已知工作总量和工作时间,怎样求工作效率?
工作效率
=
工作总量÷工作时间
探究点
1
正比例的意义和正比例关系的判断方法
数量/m
1
2
3
4
5
6
7
8
…
总价/元
3.5
7
10.5
14
17.5
21
24.5
28
…
文具店有一种彩带,销售的数量与总价的关系如下表。
你得到了哪些信息?
数量/m
1
2
3
4
5
6
7
8
…
总价/元
3.5
7
10.5
14
17.5
21
24.5
28
…
说一说:表中有哪两种量?
数量和总价
总价和数量是两种相关联的量
数量增加,总价随着增加。
数量减少,总价随着减少。
从表中你还能知道什么?
相对应的总价和数量的比的比值是一定的。
单价是固定不变的量,也就是单价一定。
比值是3.5,实际就是彩带的单价。用式子表示为:
=单价
数量/m
1
2
3
4
5
6
7
8
…
总价/元
3.5
7
10.5
14
17.5
21
24.5
28
…
3.5
3.5
3.5
3.5
3.5
3.5
3.5
3.5
…
=
=
=
=
=
=
=
=
数量/m
1
2
3
4
5
6
7
8
…
总价/元
3.5
7
10.5
14
17.5
21
24.5
28
…
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫正比例关系。
本题总价和数量是成正比例的量,总价与数量成正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
x
y
=
k(一定)
两种量成正比例关系要满足以下三个条件:
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的比值(也就是商)一定。
小试牛刀
n
0
1
2
3
4
5
6
…
2n
0
2
4
…
1.用n表示自然数,把下表填写完成。(选题源于教材P50第6题)
6
8
10
12
探究点
2
正比例图象的特点
根据图象回答下面的问题:
0
2
4
6
8
10
12
14
7
14
21
28
35
42
49
(1)从图中你发现了什么?
答:这个图象是一条逐渐上升的直的线。
总价/元
数量/m
总价/元
数量/m
0
2
4
6
8
10
12
14
7
14
21
28
35
42
49
答:这两个点也在这条射线上,并且射线又在上升,它们的单价相等。
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象连起来并延长,你还能发现什么?
总价/元
数量/m
0
2
4
6
8
10
12
14
7
14
21
28
35
42
49
(3)不计算,根据图象判断,如果买9
m彩带,总价是多少?49元能买多少米彩带?
答:通过观察,我发现买9
m彩带总价是31.5元,49元能买14
m彩带。
31.5
总价/元
数量/m
0
2
4
6
8
10
12
14
7
14
21
28
35
42
49
31.5
(4)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?
答:因为彩带的数量成倍地增加,总价也会成倍地增加,所以他花的钱是小丽的2倍。
彩带的单价一定
你能举出生活中正比例关系的例子吗?
正方形的周长与边长成正比例关系。
如果汽车行驶速度一定,路程与时间成正比例关系。
1.填空。
(1)为提高自身的阅读能力,学生们积极订阅书刊,认真阅读。某书店销售《小学生天地》的份数和总价如下表:
①表中( )和( )是相关联的量,( )增加,( )也随着增加。
份数
份数/份
1
2
3
4
5
6
…
总价/元
30
60
90
120
150
180
…
总价
份数
总价
②总价与份数这两个相关联的量中相对应的两个数的比值都是( ),这个比值实际上是( )。
③因为总价与份数的比值一定,所以表中的两种量叫做成( )的量。
(2)
路程与时间的比值是( ),当这个比值一定时,
( )和( )成( )比例关系。
正比例
速度
路程
时间
正
30
《小学生天地》的单价
2.判断。(对的画“√”,错的画“×”)
(1)长方形的长一定,宽和面积成正比例关系。
( )
(2)正方形的面积与边长成正比例关系。
( )
(3)比的前项一定,比的后项和比值成正比例关系。
( )
(4)x÷y=4,x和y成正比例关系。
( )
3.选择。(将正确答案的字母填在括号里)
(1)
下列各组中两种量不成正比例关系的是( )。
A.人的身高与年龄
B.y=5x,y和x
C.工作效率一定,工作总量和工作时间
D.圆的周长与直径
A
(2)
甲数的
与乙数的
相等(甲、乙均不为0),甲数与乙数(
)。
A.成正比例关系
B.不成正比例关系
C.无法判断
A
4.一辆汽车行驶的时间和路程如下表。
(选题源于教材P46做一做)
时间/时
1
2
3
4
5
6
路程/km
80
160
240
320
400
480
(1)写出几组路程与相对应的时间的比,并比较比值的大小。
80
∶1
160
∶2
240
∶3
320
∶4
400
∶5
480
∶6
比值相等(一定)。
(2)说一说这个比值表示什么。
这个比值表示速度。
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例关系。因为路程随着时间的变化而变化,而且
=速度(一定),所以成正比例关系。
路程
时间
(4)在图中描出表示路程和相对应时间的点,然后把它们按顺序连起来。并估计一下行驶120
km大约要用多少时间。
行驶120
km大约要用1.5时。
5.判断下面各题中的两种量是否成正比例关系,并说明理由。
(1)三角形的底一定,面积和高。
(2)成活率一定,栽树的棵数和成活的棵数。
(3)圆的面积和它的半径。
不成比例关系。
理由:
=π×半径
6.在梯形中,面积和哪种量成正比例关系?
如果梯形的高一定,那么面积与上下底的和成正比例关系;如果梯形的上下底的和一定,那么面积与高成正比例关系。
辨析:要正确理解正比例关系。
这节课你有哪些收获?
正比例:
1.
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
判断两个量是否成正比例关系的基本步骤:
首先判断两个量是不是相关联的量。
然后再看两个量的商是否为定值。
正比例图象的特点:
正比例关系的图象是一条直的线。从图象中可以直观地看到相对应两种量的变化情况。不用计算,由一种量的值可以直接找到相对应的另一种量的值。
作
业
请完成教材第49页练习九第1题、第2题、第3题、第4题、第5题。
thank
you!
