14.1.2直角三角形的判定课件
图片预览






文档简介
(共18张PPT)
直角三角形有哪些性质?
(1)有一个角是直角;
(2)两个锐角的和为90°(互余 );
(3)两直角边的平方和等于斜边的平方 ;
想想: 一个三角形满足什么条件,
才能是直角三角形呢
回顾
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
想想:
如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形吗
一个三角形应满足什么条件才能是直角三角形
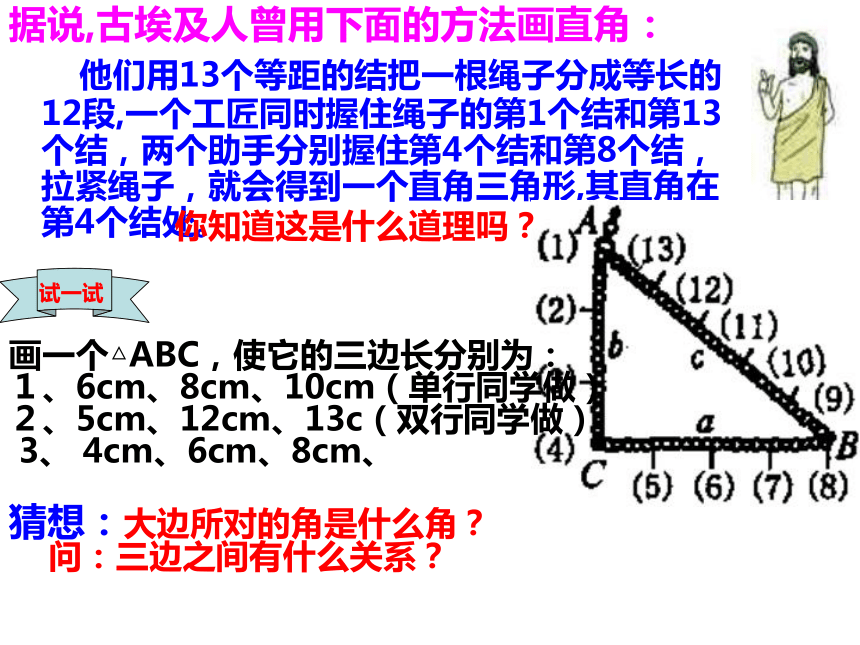
据说,古埃及人曾用下面的方法画直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
试一试
画一个△ABC,使它的三边长分别为:
1、6cm、8cm、10cm(单行同学做)
2、5cm、12cm、13c(双行同学做)
3、 4cm、6cm、8cm、
猜想:大边所对的角是什么角?
问:三边之间有什么关系?
你知道这是什么道理吗?
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 。
a2 + b2 = c2
如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
反过来
逆定理:
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较小边长的平方和是否等于最大边长的平方.
1、判断由线段a,b,c组成的三角形是不是直角三角形
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为15
∵132+142=169+196=365
152 =225
∴132+ 142 ≠ 152
∴以13, 15, 14为边长的三角形不是直角三角形
像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数.
大家一起来:
2、下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a=9 b=40 c=41 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
1、已知:在△ ABC中, AB=15cm,AC=20cm,
BC=25cm,AD是BC边上的高。求: AD的长。
2. 满足下列条件△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5
D
3.下列各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52 C. 5,11,12 D. 5,12,13
D
试试看:
B
A、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形
1.如图,两个正方形的面积分别为64,49,则AC=( )
A
D
C
64
49
2.由四根木棒,长度分别为3,4,5,12,13 若去其中三根木棒组呈三角形,有( )种取法,其中,能构成直角三角形的是( )种取法。
17
4
2
你能行:
1.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,此三角形为_____三角形.
2.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则 2 CD2 + AD2 +BD2 =____;
直角
1
考考你:
3、如果△ABC的三边长分别为 a,b,c,且a=m2-n2,
b=2mn,c=m2+n2(m>n,m,n是正整数,
则△ABC是直角三角形
解:∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=m4+2m2n2+n4
=(m2+n2)2
=c2
∴△ABC是直角三角形。
∵ S △ ABC= AC AB
= BC AD
∴ AD=
1、已知:在△ ABC中, AB=15cm,AC=20cm,
BC=25cm,AD是BC边上的高。求: AD的长。
练习
解: ∵ AB=15cm,AC=20cm,BC=25cm
∴ AB2+AC2=225+400=625
BC2=625
∴ AB2+AC2=BC2
∴ ∠ BAC=900(勾股定理的逆定理)
15
20
25
4、已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
S四边形ABCD=36
3
4
12
13
5
∟
1、勾股定理的逆定理的内容。
2、应用该定理的基本步骤。
3、判定一个三角形是直角三角形有哪 些方法(从角、边两个方面来总结)。
4、勾股定理与它的逆定理之间的关系。
课堂小结:
通过本节课的学习,同学们有哪些收获?
1、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
思考:
2、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园 请通过计算说明.
A
B
C
400
1000
60°
30°
D
如图:边长为4的正方形ABCD中,F是DC的中
点,且CE= BC,则AF⊥EF,试说明理由
解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC
∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25
∴AD=4,DF=2,FC=2,EC=1
∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF
A
3、
直角三角形有哪些性质?
(1)有一个角是直角;
(2)两个锐角的和为90°(互余 );
(3)两直角边的平方和等于斜边的平方 ;
想想: 一个三角形满足什么条件,
才能是直角三角形呢
回顾
(1)有一个角是直角的三角形是直角三角形;
(2)有两个角的和是90°的三角形是直角三角形;
想想:
如果一个三角形的三边a ,b ,c 满足a2 +b 2=c2 ,
那么这个三角形是直角三角形吗
一个三角形应满足什么条件才能是直角三角形
据说,古埃及人曾用下面的方法画直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。
试一试
画一个△ABC,使它的三边长分别为:
1、6cm、8cm、10cm(单行同学做)
2、5cm、12cm、13c(双行同学做)
3、 4cm、6cm、8cm、
猜想:大边所对的角是什么角?
问:三边之间有什么关系?
你知道这是什么道理吗?
勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么 。
a2 + b2 = c2
如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。
a2 + b2 = c2
反过来
逆定理:
分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较小边长的平方和是否等于最大边长的平方.
1、判断由线段a,b,c组成的三角形是不是直角三角形
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∴152+82 =172
∴以15, 8, 17为边长的三角形是直角三角形
(2)最大边为15
∵132+142=169+196=365
152 =225
∴132+ 142 ≠ 152
∴以13, 15, 14为边长的三角形不是直角三角形
像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数.
大家一起来:
2、下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
(4) a=9 b=40 c=41 _____ _____ ;
是
是
不是
是
∠ A=900
∠ B=900
∠ C=900
(3) a=1 b=2 c= ____ _____ ;
1、已知:在△ ABC中, AB=15cm,AC=20cm,
BC=25cm,AD是BC边上的高。求: AD的长。
2. 满足下列条件△ABC,不是直角三角形的是( )
A.b2=a2-c2 B. a:b:c=3:4:5
C.∠C=∠A-∠B D. ∠A:∠B : ∠C =3:4:5
D
3.下列各组线段中,能组成直角三角形的是( )
A. 5,6,7 B. 32,42,52 C. 5,11,12 D. 5,12,13
D
试试看:
B
A、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形
1.如图,两个正方形的面积分别为64,49,则AC=( )
A
D
C
64
49
2.由四根木棒,长度分别为3,4,5,12,13 若去其中三根木棒组呈三角形,有( )种取法,其中,能构成直角三角形的是( )种取法。
17
4
2
你能行:
1.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,此三角形为_____三角形.
2.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则 2 CD2 + AD2 +BD2 =____;
直角
1
考考你:
3、如果△ABC的三边长分别为 a,b,c,且a=m2-n2,
b=2mn,c=m2+n2(m>n,m,n是正整数,
则△ABC是直角三角形
解:∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=m4+2m2n2+n4
=(m2+n2)2
=c2
∴△ABC是直角三角形。
∵ S △ ABC= AC AB
= BC AD
∴ AD=
1、已知:在△ ABC中, AB=15cm,AC=20cm,
BC=25cm,AD是BC边上的高。求: AD的长。
练习
解: ∵ AB=15cm,AC=20cm,BC=25cm
∴ AB2+AC2=225+400=625
BC2=625
∴ AB2+AC2=BC2
∴ ∠ BAC=900(勾股定理的逆定理)
15
20
25
4、已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
S四边形ABCD=36
3
4
12
13
5
∟
1、勾股定理的逆定理的内容。
2、应用该定理的基本步骤。
3、判定一个三角形是直角三角形有哪 些方法(从角、边两个方面来总结)。
4、勾股定理与它的逆定理之间的关系。
课堂小结:
通过本节课的学习,同学们有哪些收获?
1、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
思考:
2、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园 请通过计算说明.
A
B
C
400
1000
60°
30°
D
如图:边长为4的正方形ABCD中,F是DC的中
点,且CE= BC,则AF⊥EF,试说明理由
解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC
∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25
∴AD=4,DF=2,FC=2,EC=1
∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF
A
3、
