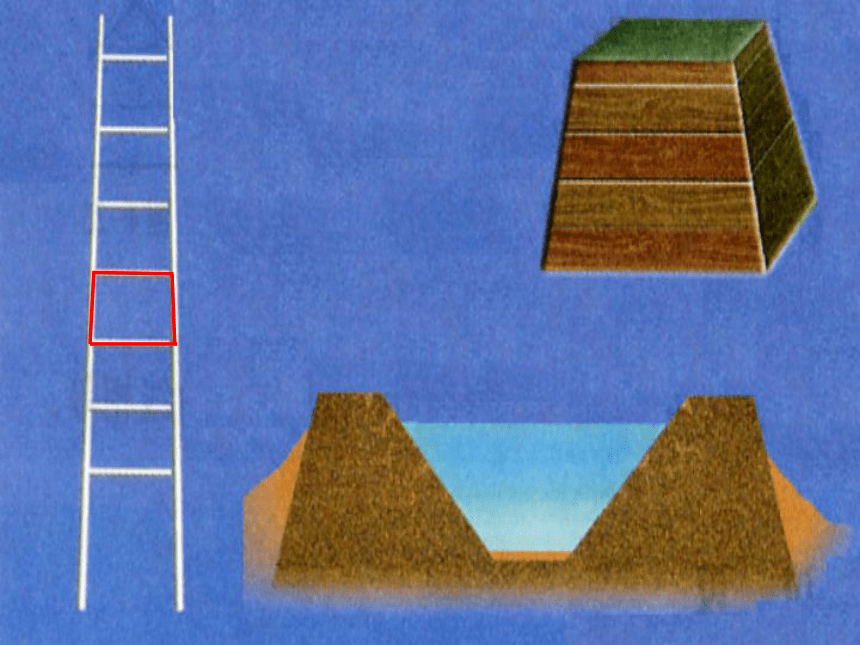
梯形

(共24张PPT)
梯形(一)
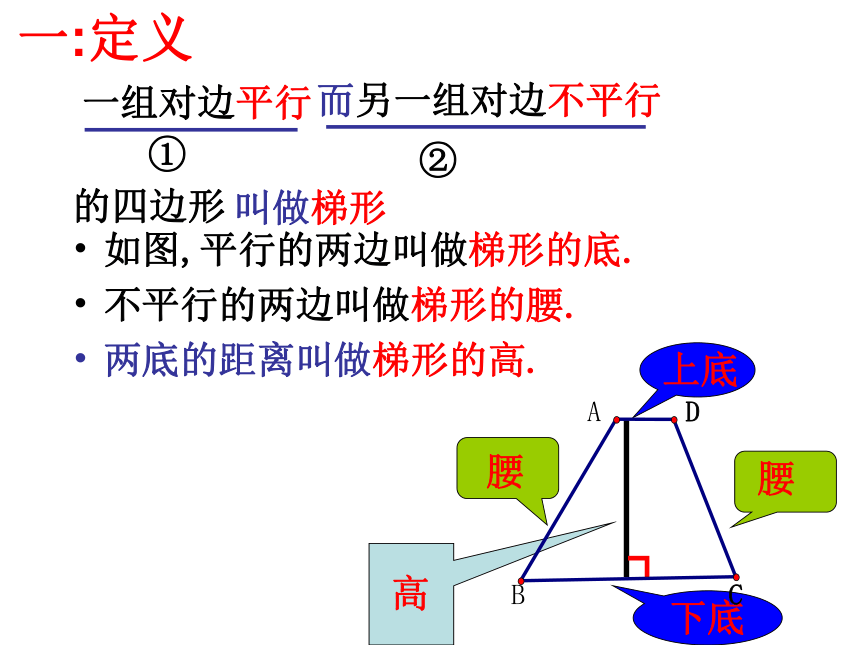
一:定义
上底
下底
如图,平行的两边叫做梯形的底.
不平行的两边叫做梯形的腰.
两底的距离叫做梯形的高.
腰
腰
┓
高
一组对边平行
而另一组对边不平行
的四边形
叫做梯形
B
C
A
D
①
②
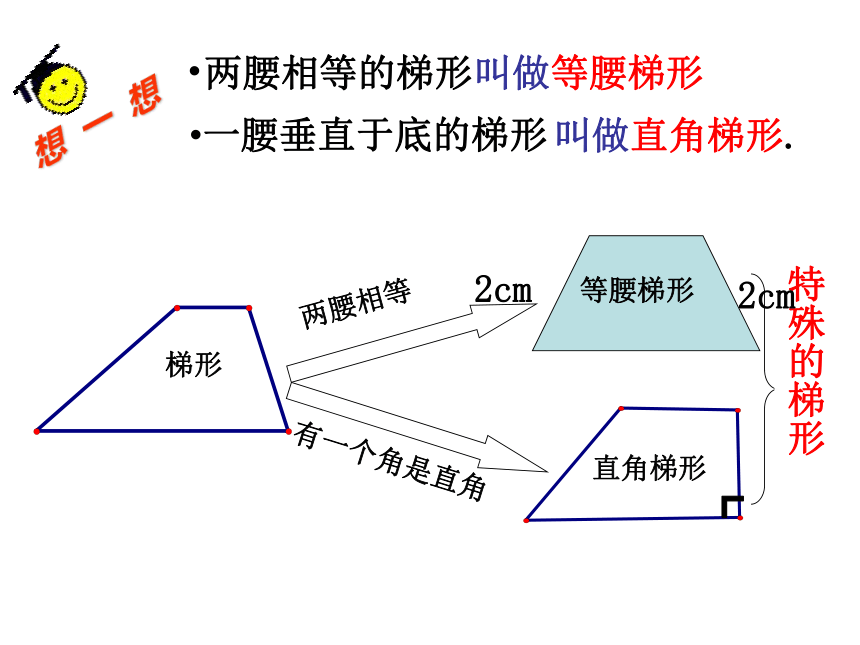
两腰相等
有一个角是直角
梯形
直角梯形
特殊的梯形
想 一 想
┗
2cm
2cm
两腰相等的梯形
叫做等腰梯形
一腰垂直于底的梯形
叫做直角梯形.
等腰梯形
1. 判断:
(1)有一组对边平行的四边形是梯形. ( )
(2)有一组对边平行但不相等的四边形是梯形. ( )
(3)一组对边平行,且有一个角是直角的四边形是
直角梯形. ( )
√
×
×
练一练
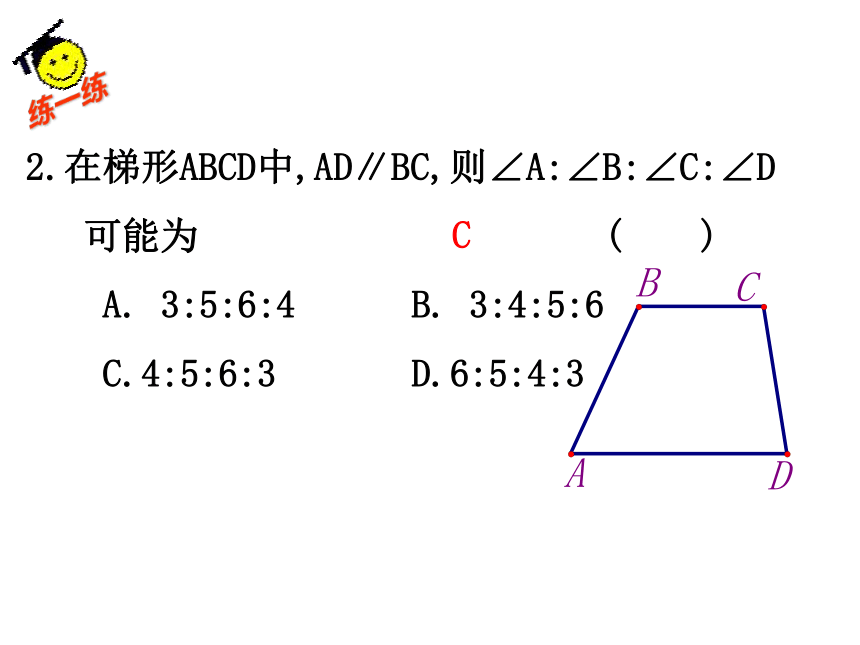
2.在梯形ABCD中,AD∥BC,则∠A:∠B:∠C:∠D
可能为 ( )
A. 3:5:6:4 B. 3:4:5:6
C.4:5:6:3 D.6:5:4:3
C
练一练
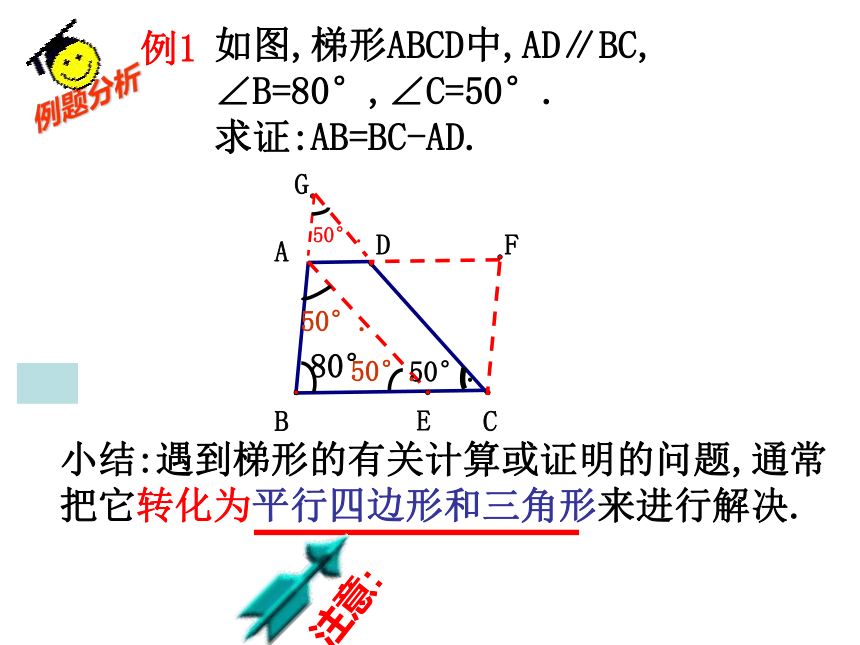
如图,梯形ABCD中,AD∥BC,
∠B=80°,∠C=50°.
求证:AB=BC-AD.
B
C
A
D
例题分析
G
E
F
小结:遇到梯形的有关计算或证明的问题,通常
把它转化为平行四边形和三角形来进行解决.
注意:
80°
50°.
50°.
50°.
50°.
例1
练一练
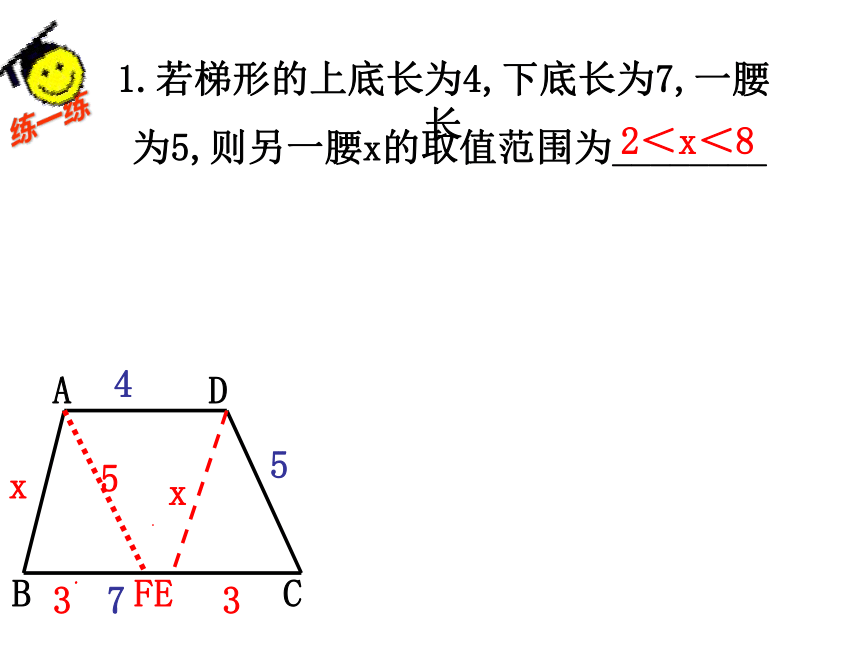
1.若梯形的上底长为4,下底长为7,一腰长
2＜x＜8
4
7
5
x
x
3
A
B
C
D
E
5
F
3
为5,则另一腰x的取值范围为________
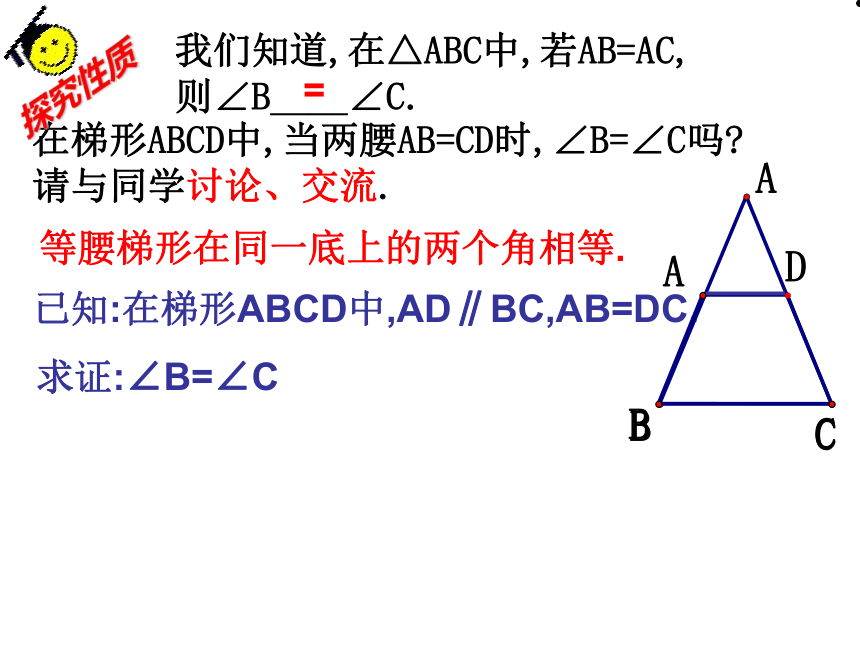
在梯形ABCD中,当两腰AB=CD时,∠B=∠C吗 请与同学讨论、交流.
等腰梯形在同一底上的两个角相等.
已知:在梯形ABCD中,AD∥BC,AB=DC.
我们知道,在△ABC中,若AB=AC,
则∠B____∠C.
=
求证:∠B=∠C
探究性质
B
C
A
等腰梯形的性质
等腰梯形在同一底上的两个角相等.
已知：梯形ABCD中，AD//BC，AB=DC.
求证： ∠B= ∠C
A
B
C
D
E
F
E
A
D
C
B
A
D
C
B
探究性质
E
等腰梯形的性质定理
等腰梯形在同一底上的两个角相等.
所用的辅助线为:
符号语言:
梯形ABCD, AD//BC
AB=CD
∠ B= ∠ C
∠ A= ∠ D
已知：梯形ABCD中，AD//BC，AB=CD
求证： ∠B= ∠C
平移一腰
加高
E
F
C
A
D
B
∟
1
2
3
x
x
2x
且对角线BD⊥CD.
(1)求∠C的度数.
变式练习一:
例题分析
(2)若此时梯形的周长为30cm.
求梯形的各边的长.
变式练习二:
如上图,梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥CD,且梯形ABCD的 周长为30,求腰长.
例2.
已知:梯形ABCD中,AD∥BC,AD=AB=CD
求证:等腰梯形下底的中点与两腰的距离相等.
练一练
已知:梯形ABCD中,AD∥BC,AB=CD,E为BC的中点,EF⊥AB,EG⊥CD,垂足分别为F、G.
求证:EF=EG
G
F
D
E
B
C
A
┗
┗
探究二:
等腰梯形的两条对角线大小有怎样的关系呢
等腰梯形的两条对角线相等
已知：梯形ABCD中，AD//BC，AB=DC
求证：AC=BD
梯形ABCD, AD//BC
AB=CD
AC=BD
符号语言
等腰梯形的性质
例3.已知:如图,在梯形ABCD中,AD∥BC,
例题分析
E
C
A
D
B
AB=CD,延长BC到E,使CE=AD,连结
BD、DE.
求证:BD=DE.
如图,延长等腰梯形的两腰
相交于点E.那么△EBC和
△EAD都是_____三角形.
如果过E作EF⊥BC,则
EF___AD,BF___CF.
根据等腰三角形是轴对称图形,
可得等腰梯形也是_________,
_________________是它的对称轴.
等腰
轴对称图形
经过两底中点的直线
⊥
=
D
B
C
A
E
F
探究三:
在线段、角、等边三角形、等腰梯形、平行四边形、 菱形中，既是轴对称图形又是中心对称图形的有 ( )
A.1个 B.2个 C.3个 D.4个
学力测试
B
两组对边分别平行
这节课的收获是
1.梯形、等腰梯形、直角梯形的定义:
2.等腰梯形的特有性质:
4.知识系统图:
平行四边形
四边形
……
3.等腰梯形的对称性:
梯形
一组对边平行
另一组对边不平行
等腰梯形
直角梯形
作业
P.179 (A)2,3,4