人教版数学八年级上册 13.3.1等腰三角形 课件(14张ppt)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1等腰三角形 课件(14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 868.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
八年级上册第十三章第三节
A
B
C
1.有两条边相等的三角形,叫做等腰三角形.
2.相等的两条边叫做腰,
另一条边叫做底边.
腰与底边的夹角叫做底角.
3.两腰的夹角叫做顶角,
腰
腰
底边
顶角
底角
底角
回顾思考
引入新课
学习目标
1.知道等腰三角形的基本概念,并会运用不同方法推导等腰三角形的性质.
2.能初步运用等腰三角形的性质解决有关问题.
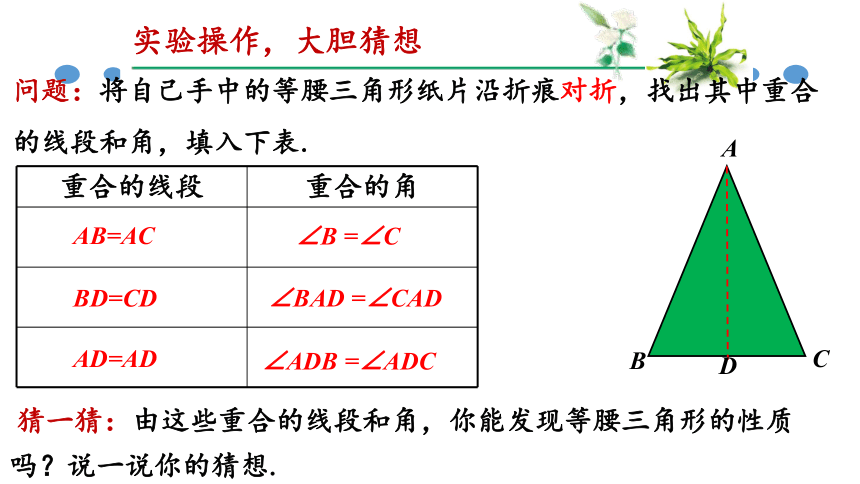
实验操作,大胆猜想
问题:将自己手中的等腰三角形纸片沿折痕对折,找出其中重合的线段和角,填入下表.
A
C
B
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD
=∠CAD
∠ADB
=∠ADC
猜一猜:由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
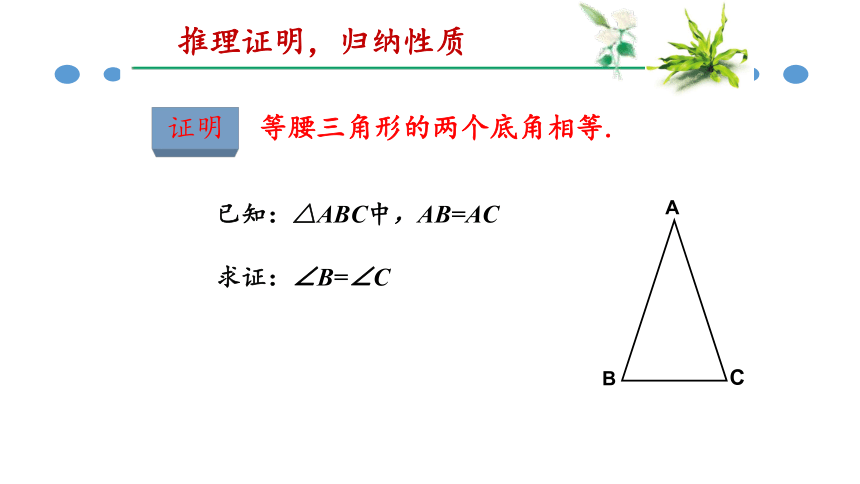
证明
等腰三角形的两个底角相等.
A
B
C
已知:△ABC中,AB=AC
求证:∠B=∠C
推理证明,归纳性质
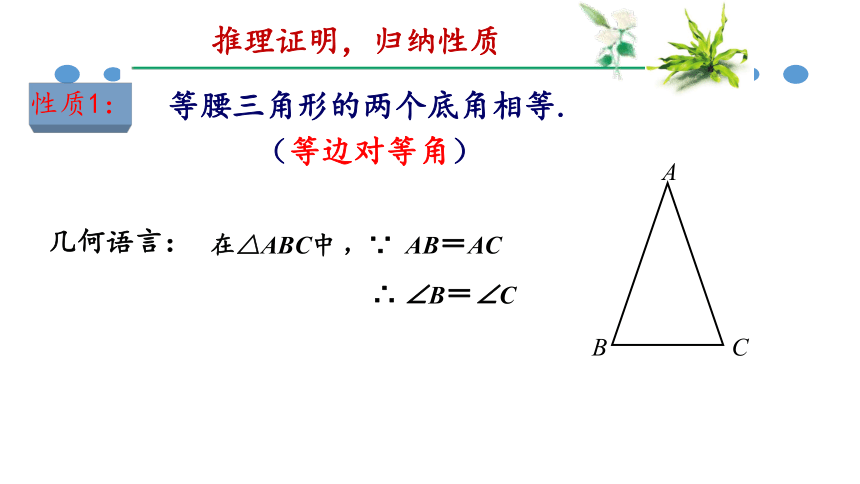
性质1:
等腰三角形的两个底角相等.
A
B
C
在△ABC中
,∵
AB=AC
∴
∠B=∠C
(等边对等角)
推理证明,归纳性质
几何语言:
(3)∵AB=AC,AD⊥BC,
∴∠___=∠___,___=____;
1
2
BD
CD
性质2:
(简写成“三线合一”
)
等腰三角形的顶角平分线,底边上的中线,底边上的高相互重合.
推理证明,归纳性质
几何语言:
(2)∵AB=AC,
BD=CD
,
∴∠___=∠___,___⊥____;
1
2
AD
BC
(1)∵AB=AC,
∠1=∠2,
∴___
=
___,___⊥____.
BD
AD
BC
CD
A
B
C
D
1
2
巩固练习,熟悉性质
1.在△ABC
中,AB=AC,如果一个底角为50°,则另外两个角为____和____.
50°
80°
A
B
C
2.在△ABC
中,AB=AC,如果一个角为50°,则另外两个角为________________________.
50°和
80°
或
65°和
65
°
3.在△ABC
中,AB=AC,如果一个角为110°,则另外两个角为________________________.
35°和
35°
4.在
△ABC中,AB=AC,点D是BC的中点,∠B
=
40°,则∠BAD
的度数是
.
50°
巩固练习,熟悉性质
D
C
B
A
性质应用,例题精讲
(2)用含∠A的式子分别表示出∠BDC、∠C、∠ABC?
(3)设∠A=x,请把△
ABC的内角和用含x的方程表示出来?
(1)图中有哪些等腰三角形?找出图中所有相等的角?
例1:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求△ABC
各角的度数?
在△ABC中,∠A+∠ABC+∠C=x+2x+2x=180°.
解得
x=36°,
∴
在△ABC中,∠A=36°,∠ABC=∠C=72°
解:
∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC
∠A=∠ABD(等边对等角)
设∠A=x,则∠BDC=∠A+∠ABD=2x
∴∠ABC=∠C=∠BDC=2x
性质应用,例题精讲
D
C
B
A
例1:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求△ABC
各角的度数?
变式训练
强化性质
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解:∵
AB=AD=DC
∴∠B=∠ADB,∠C=∠DAC
设∠C=x,则∠DAC=x,
在△ABD中,根据三角形内角和定理,得
2x+2x+26°=180°,
解得x=38.5°.
∴
∠C=
x=38.5°,
∠B=2x=77°.
∠B=∠ADB=∠C+∠DAC=2x,
回归总结,升华目标
等腰三角形
的主要特征
②从角看-------
①从边看-----
③从“三线”看----
④从整体看-------
①转化思想
分类思想
方程思想
两边相等
两个底角相等
顶角的平分线
底边上的中线
底边上的高相互重合
(三线合一)
轴对称图形
②等腰三角形常用的辅助线
顶角平分线、底边中线,底边的高
1.知识方面
2.方法方面
分层开放
布置作业
1、必做题:课本第81页第1、4、7题
2、选做题:课本第83页第13题
八年级上册第十三章第三节
A
B
C
1.有两条边相等的三角形,叫做等腰三角形.
2.相等的两条边叫做腰,
另一条边叫做底边.
腰与底边的夹角叫做底角.
3.两腰的夹角叫做顶角,
腰
腰
底边
顶角
底角
底角
回顾思考
引入新课
学习目标
1.知道等腰三角形的基本概念,并会运用不同方法推导等腰三角形的性质.
2.能初步运用等腰三角形的性质解决有关问题.
实验操作,大胆猜想
问题:将自己手中的等腰三角形纸片沿折痕对折,找出其中重合的线段和角,填入下表.
A
C
B
D
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B
=∠C
∠BAD
=∠CAD
∠ADB
=∠ADC
猜一猜:由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
证明
等腰三角形的两个底角相等.
A
B
C
已知:△ABC中,AB=AC
求证:∠B=∠C
推理证明,归纳性质
性质1:
等腰三角形的两个底角相等.
A
B
C
在△ABC中
,∵
AB=AC
∴
∠B=∠C
(等边对等角)
推理证明,归纳性质
几何语言:
(3)∵AB=AC,AD⊥BC,
∴∠___=∠___,___=____;
1
2
BD
CD
性质2:
(简写成“三线合一”
)
等腰三角形的顶角平分线,底边上的中线,底边上的高相互重合.
推理证明,归纳性质
几何语言:
(2)∵AB=AC,
BD=CD
,
∴∠___=∠___,___⊥____;
1
2
AD
BC
(1)∵AB=AC,
∠1=∠2,
∴___
=
___,___⊥____.
BD
AD
BC
CD
A
B
C
D
1
2
巩固练习,熟悉性质
1.在△ABC
中,AB=AC,如果一个底角为50°,则另外两个角为____和____.
50°
80°
A
B
C
2.在△ABC
中,AB=AC,如果一个角为50°,则另外两个角为________________________.
50°和
80°
或
65°和
65
°
3.在△ABC
中,AB=AC,如果一个角为110°,则另外两个角为________________________.
35°和
35°
4.在
△ABC中,AB=AC,点D是BC的中点,∠B
=
40°,则∠BAD
的度数是
.
50°
巩固练习,熟悉性质
D
C
B
A
性质应用,例题精讲
(2)用含∠A的式子分别表示出∠BDC、∠C、∠ABC?
(3)设∠A=x,请把△
ABC的内角和用含x的方程表示出来?
(1)图中有哪些等腰三角形?找出图中所有相等的角?
例1:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求△ABC
各角的度数?
在△ABC中,∠A+∠ABC+∠C=x+2x+2x=180°.
解得
x=36°,
∴
在△ABC中,∠A=36°,∠ABC=∠C=72°
解:
∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC
∠A=∠ABD(等边对等角)
设∠A=x,则∠BDC=∠A+∠ABD=2x
∴∠ABC=∠C=∠BDC=2x
性质应用,例题精讲
D
C
B
A
例1:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求△ABC
各角的度数?
变式训练
强化性质
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解:∵
AB=AD=DC
∴∠B=∠ADB,∠C=∠DAC
设∠C=x,则∠DAC=x,
在△ABD中,根据三角形内角和定理,得
2x+2x+26°=180°,
解得x=38.5°.
∴
∠C=
x=38.5°,
∠B=2x=77°.
∠B=∠ADB=∠C+∠DAC=2x,
回归总结,升华目标
等腰三角形
的主要特征
②从角看-------
①从边看-----
③从“三线”看----
④从整体看-------
①转化思想
分类思想
方程思想
两边相等
两个底角相等
顶角的平分线
底边上的中线
底边上的高相互重合
(三线合一)
轴对称图形
②等腰三角形常用的辅助线
顶角平分线、底边中线,底边的高
1.知识方面
2.方法方面
分层开放
布置作业
1、必做题:课本第81页第1、4、7题
2、选做题:课本第83页第13题
