人教版数学八年级上册 13.3.1等腰三角形的性质 课件(19张ppt)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1等腰三角形的性质 课件(19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 20:19:41 | ||
图片预览



文档简介
(共19张PPT)
第十三章
轴对称
13.3
等腰三角形
第1课时
等腰三角形的性质
等腰三角形边角性质:等边对等角
等腰三角形的轴对称性:“三线合一”
知1-导
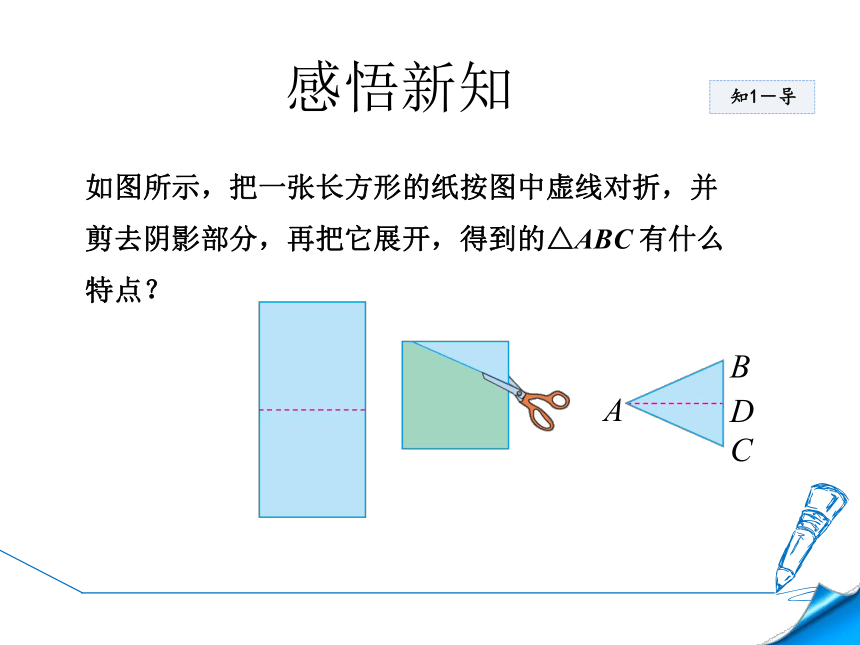
如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC
有什么
特点?
A
B
C
D
感悟新知
知1-导
仔细观察自己剪出的等腰三角形纸片,你能
发现这
个等腰三角形有什么特征吗?
等腰三角形的特征:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合.
知1-导
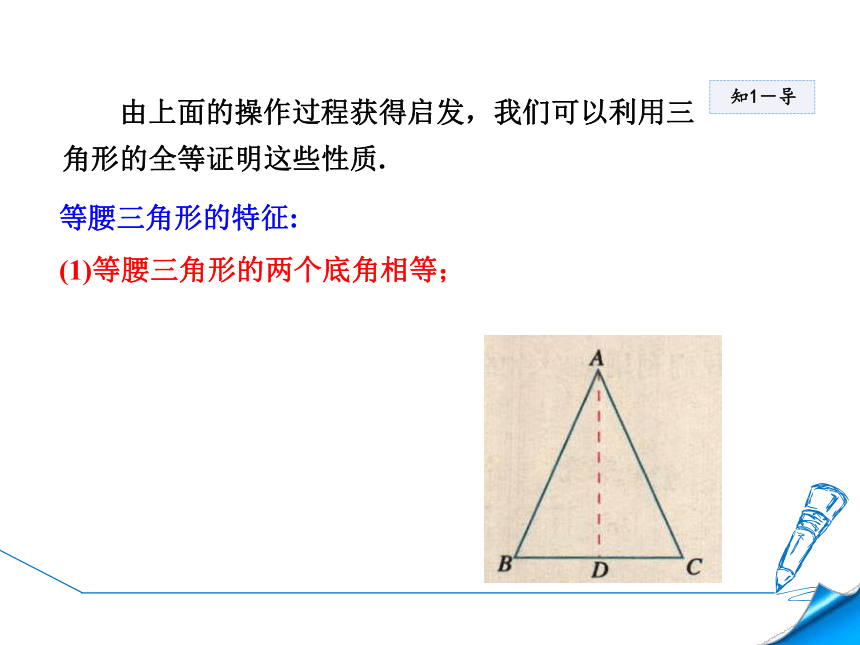
由上面的操作过程获得启发,我们可以利用三
角形的全等证明这些性质.
等腰三角形的特征:
(1)等腰三角形的两个底角相等;
知1-导
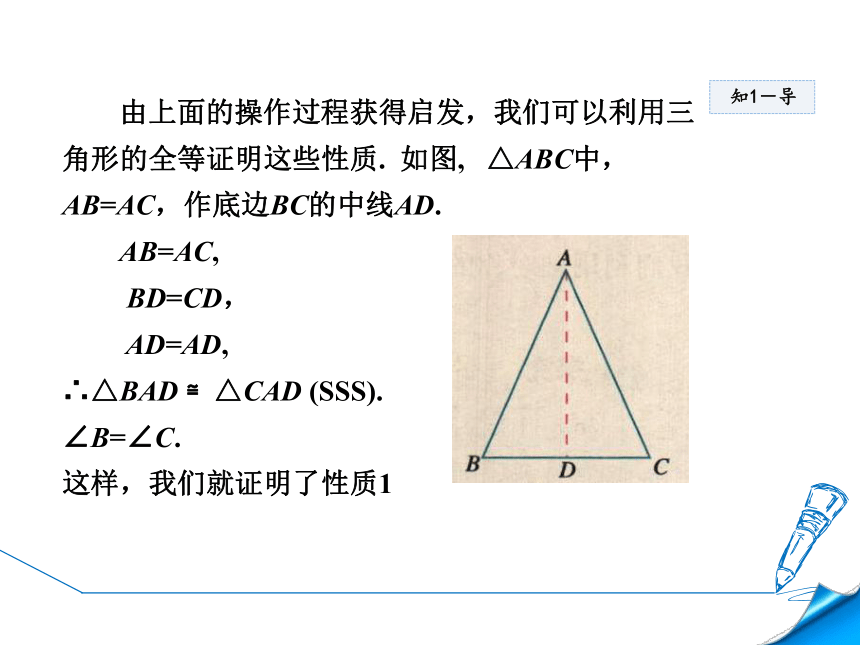
由上面的操作过程获得启发,我们可以利用三
角形的全等证明这些性质.
如图,
△ABC中,
AB=AC,作底边BC的中线AD.
AB=AC,
BD=CD,
AD=AD,
∴△BAD
≌△CAD
(SSS).
∠B=∠C.
这样,我们就证明了性质1
知1-导
归
纳
我们可以发现等腰三角形的性质:
性质1
等腰三角形的两个底角相等(简写成“等边
对顶角”.
例1
如图,在△ABC中,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数.
知1-讲
例1
如图,在△ABC中,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数.
解:∵
AB=AC,
BD=BC=AD,
∴
∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角).
设∠A=x,则
∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+
∠ABC+∠C=x+2x+2x=180°.
解得x=36°.
所以,在△ABC
中,∠A=36°,
∠ABC=∠C=72°.
知1-讲
(来自教材)
如图,在下列等腰三角形中,分别求出它们的底
角的度数.
知1-练
如图,在下列等腰三角形中,分别求出它们的底
角的度数.
知1-练
解:(1)72°;
(2)30°.
2
知识点
等腰三角形的轴对称性:“三线合一”
知2-导
探究
把剪出的等腰三角形ABC沿折痕对折,找出其中
重合的线段和角.
由这些重合的线段和角,你能发现等腰三角形的
性质吗?说一说你的
猜想.
在一张白纸上任意画一个等腰三角形,把它剪下
来,请你试着折一
折.你的猜想仍然成立吗?
(来自教材)
知2-导
归
纳
性质2
等腰三角形的顶角平分线、底边上的中线、
底边上的高相互重合(简写成“三线合一”)
知2-讲
例2
如图,在△ABC中,AB=AC,AD是BC边上
的中线,∠ABC的平分线BG交AC于点G,交
AD于点E,EF⊥AB,垂足为F.
(1)若∠BAD=25°,求∠C的度数;
(2)求证:EF=ED.
(1)解:∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,∴∠BAC=2∠BAD=50°.
∵AB=AC,
∴
∠C=∠ABC
=
(180°-
∠A)
=
(180°-50°)=65°.
(2)证明:∵AB=AC,AD是BC边上的中线,
∴ED⊥BC,
又∵BG平分∠ABC,EF⊥AB,
∴EF=ED.
知2-讲
总
结
知2-讲
(1)等腰三角形的“三线合一”的性质是证明角相等、
线段相等和垂直关系的既重要又简便的方法.
(2)在等腰三角形中,作“三线”中“一线”,利用
“三线合一”是等腰三角形中常用的方法.
这节课我们主要探讨了等腰三角形的性质,并对
性质作了简单的应用.等腰三角形是轴对称图形,它
的两个底角相等(等边对等角),等腰三角形的对称
轴是它顶角的平分线,并且它的顶角平分线既是底边
上的中线,又是底边上的高.
1.必做:
习题13.3
1-4题(教材第81-82页)
第十三章
轴对称
13.3
等腰三角形
第1课时
等腰三角形的性质
等腰三角形边角性质:等边对等角
等腰三角形的轴对称性:“三线合一”
知1-导
如图所示,把一张长方形的纸按图中虚线对折,并
剪去阴影部分,再把它展开,得到的△ABC
有什么
特点?
A
B
C
D
感悟新知
知1-导
仔细观察自己剪出的等腰三角形纸片,你能
发现这
个等腰三角形有什么特征吗?
等腰三角形的特征:
(1)等腰三角形的两个底角相等;
(2)等腰三角形的顶角平分线、底边上的中线、底
边上的高互相重合.
知1-导
由上面的操作过程获得启发,我们可以利用三
角形的全等证明这些性质.
等腰三角形的特征:
(1)等腰三角形的两个底角相等;
知1-导
由上面的操作过程获得启发,我们可以利用三
角形的全等证明这些性质.
如图,
△ABC中,
AB=AC,作底边BC的中线AD.
AB=AC,
BD=CD,
AD=AD,
∴△BAD
≌△CAD
(SSS).
∠B=∠C.
这样,我们就证明了性质1
知1-导
归
纳
我们可以发现等腰三角形的性质:
性质1
等腰三角形的两个底角相等(简写成“等边
对顶角”.
例1
如图,在△ABC中,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数.
知1-讲
例1
如图,在△ABC中,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数.
解:∵
AB=AC,
BD=BC=AD,
∴
∠ABC=∠C=∠BDC,
∠A=∠ABD(等边对等角).
设∠A=x,则
∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x.
于是在△ABC中,有
∠A+
∠ABC+∠C=x+2x+2x=180°.
解得x=36°.
所以,在△ABC
中,∠A=36°,
∠ABC=∠C=72°.
知1-讲
(来自教材)
如图,在下列等腰三角形中,分别求出它们的底
角的度数.
知1-练
如图,在下列等腰三角形中,分别求出它们的底
角的度数.
知1-练
解:(1)72°;
(2)30°.
2
知识点
等腰三角形的轴对称性:“三线合一”
知2-导
探究
把剪出的等腰三角形ABC沿折痕对折,找出其中
重合的线段和角.
由这些重合的线段和角,你能发现等腰三角形的
性质吗?说一说你的
猜想.
在一张白纸上任意画一个等腰三角形,把它剪下
来,请你试着折一
折.你的猜想仍然成立吗?
(来自教材)
知2-导
归
纳
性质2
等腰三角形的顶角平分线、底边上的中线、
底边上的高相互重合(简写成“三线合一”)
知2-讲
例2
如图,在△ABC中,AB=AC,AD是BC边上
的中线,∠ABC的平分线BG交AC于点G,交
AD于点E,EF⊥AB,垂足为F.
(1)若∠BAD=25°,求∠C的度数;
(2)求证:EF=ED.
(1)解:∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD,∴∠BAC=2∠BAD=50°.
∵AB=AC,
∴
∠C=∠ABC
=
(180°-
∠A)
=
(180°-50°)=65°.
(2)证明:∵AB=AC,AD是BC边上的中线,
∴ED⊥BC,
又∵BG平分∠ABC,EF⊥AB,
∴EF=ED.
知2-讲
总
结
知2-讲
(1)等腰三角形的“三线合一”的性质是证明角相等、
线段相等和垂直关系的既重要又简便的方法.
(2)在等腰三角形中,作“三线”中“一线”,利用
“三线合一”是等腰三角形中常用的方法.
这节课我们主要探讨了等腰三角形的性质,并对
性质作了简单的应用.等腰三角形是轴对称图形,它
的两个底角相等(等边对等角),等腰三角形的对称
轴是它顶角的平分线,并且它的顶角平分线既是底边
上的中线,又是底边上的高.
1.必做:
习题13.3
1-4题(教材第81-82页)
