人教版数学八年级上册 13.3.1 等腰三角形课件(24张ppt)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1 等腰三角形课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 20:23:58 | ||
图片预览






文档简介
(共24张PPT)
12.3.1
等腰三角形
1、了解等腰三角形的概念,掌握等腰三角形的性质;
2、运用等腰三角形的性质进行证明和计算.
3、通过动手实践、观察归纳、并证明等腰三角形的性
质,培养学生的推理能力。
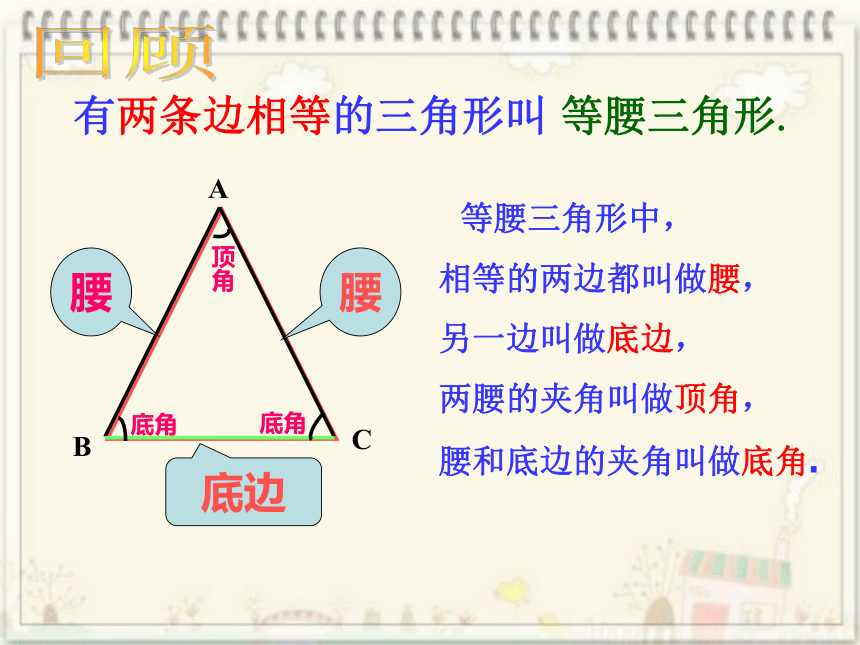
等腰三角形.
等腰三角形中,
相等的两边都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
有两条边相等的三角形叫
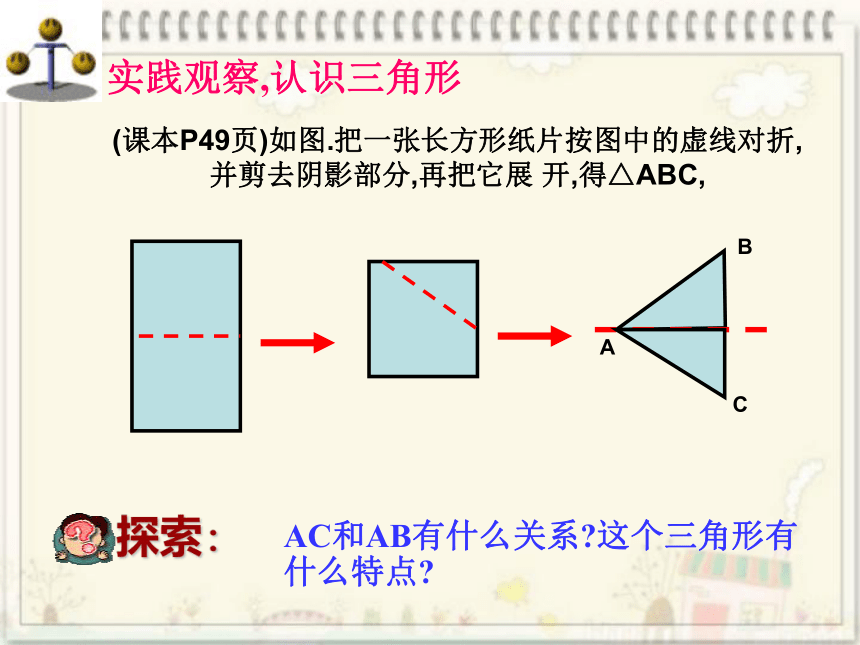
(课本P49页)如图.把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展
开,得△ABC,
实践观察,认识三角形
AC和AB有什么关系?这个三角形有什么特点?
探索:
A
B
C
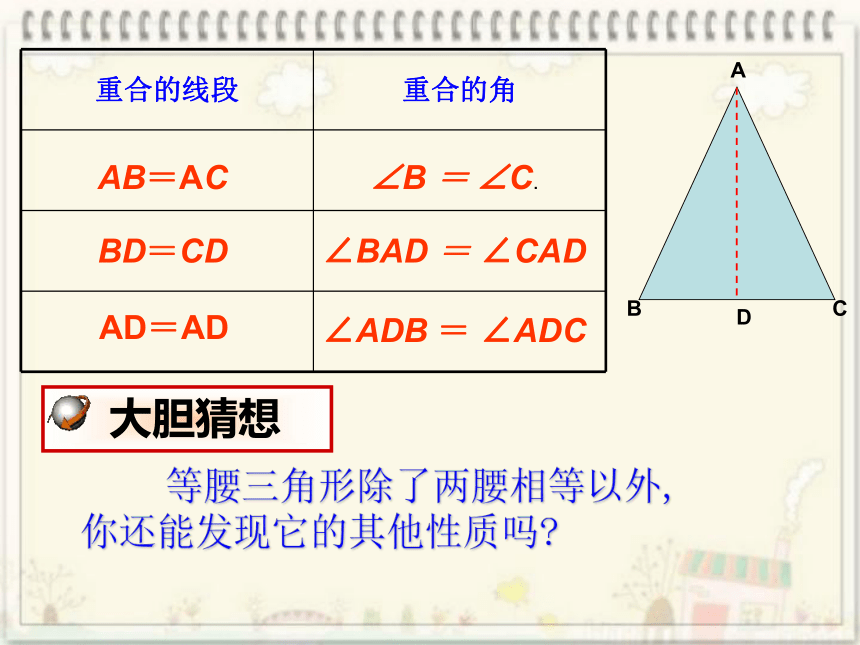
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B
=
∠C.
∠BAD
=
∠CAD
∠ADB
=
∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗?
大胆猜想
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想
A
B
C
D
D
如图,作△ABC底边的中线AD
D
┌
如图,
作△ABC
底边的高AD
D
如图,作顶角
的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
1
2
已知:如图,△ABC中,AB=AC。
求证:∠B=∠C
A
B
C
D
1
2
证明:作顶角的角平分线AD,
在△BAD和△CAD中,
AB=AC(已知)
∠1=∠2
AD=AD(公共边)
∴△BAD≌△CAD(SAS)
∴∠B=∠C(全等三角形的对应角相等)
论证
∵AB=AC
∴∠B=∠C
性质1
等腰三角形的两个底角相等。
等腰三角形的性质
符号语言
简称
等边对等角
⒈等腰三角形一个底角为70°,它的另外两个
角为_____
__;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______
__。
70°,
40°
70°,40°或55°,55°
35°,
35°
想一想:
由刚才证明的△ABD≌
△ACD,除了能得到∠B=∠C
你还能发现什么?
A
B
D
C
等腰三角形的顶角平分线,底边上的中线,底边上的高相互重合.
性质2
(简写成“三线合一”)
∴BD=CD,∠ADB=∠ADC=90°.
A
B
C
D
1
2
证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC,
∠1=∠2,
AD=AD,
∴△BAD≌△CAD
(SAS)
根据等腰三角形的性质,
在△ABC中,AB=AC时,
(1)∵AD⊥BC,
∴∠
=∠
,
=
;
(2)∵AD是中线,
∴
⊥
,
∠
=∠
;
(3)∵AD是角平分线,
∴
⊥
,
=
。
A
B
C
D
BAD
CAD
BD
CD
BAD
CAD
AD
BC
AD
BC
BD
CD
练习2
1、等腰三角形的顶角一定是锐角。
2
、等腰三角形的底角一定是锐角。
3、等腰三角形的角平分线、中线和高互相重合。
(X)
(√)
(X)
等腰三角形的角平分线、中线和高,一定重合吗?
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°
x
⌒
x
⌒
⌒
2x
例题:如图,在△ABC中
,AB=AC,点D在AC
上,且BD=BC=AD.
求△ABC各内角的度数?
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数
解:∵AB=AD=DC
∴
∠B=
∠ADB,∠C=
∠DAC
设
∠C=x,则
∠DAC=x,
∠B=
∠ADB=
∠C+
∠DAC=2x
在△ABC中,
∠B+
∠C+
∠BAD+
∠DAC
=2x+x+26°+x=180°
解得:x=38.5°,
∴
∠B=77°,
∠C=
38.5°
课本第77页练习第3题
谈谈你的收获!
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合
一”
学习的数学思想及方法:
分类讨论和一题多解。
解决等腰三角形问题时常用的辅助线
作业:
1.必做题:教科书81页第1、4、7题;
2.选做题:教科书83页第13题
结束寄语:
成功不是凭梦想和希望,而是凭努力和实践。
12.3.1
等腰三角形
1、了解等腰三角形的概念,掌握等腰三角形的性质;
2、运用等腰三角形的性质进行证明和计算.
3、通过动手实践、观察归纳、并证明等腰三角形的性
质,培养学生的推理能力。
等腰三角形.
等腰三角形中,
相等的两边都叫做腰,
另一边叫做底边,
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
有两条边相等的三角形叫
(课本P49页)如图.把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展
开,得△ABC,
实践观察,认识三角形
AC和AB有什么关系?这个三角形有什么特点?
探索:
A
B
C
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B
=
∠C.
∠BAD
=
∠CAD
∠ADB
=
∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗?
大胆猜想
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想
A
B
C
D
D
如图,作△ABC底边的中线AD
D
┌
如图,
作△ABC
底边的高AD
D
如图,作顶角
的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
1
2
已知:如图,△ABC中,AB=AC。
求证:∠B=∠C
A
B
C
D
1
2
证明:作顶角的角平分线AD,
在△BAD和△CAD中,
AB=AC(已知)
∠1=∠2
AD=AD(公共边)
∴△BAD≌△CAD(SAS)
∴∠B=∠C(全等三角形的对应角相等)
论证
∵AB=AC
∴∠B=∠C
性质1
等腰三角形的两个底角相等。
等腰三角形的性质
符号语言
简称
等边对等角
⒈等腰三角形一个底角为70°,它的另外两个
角为_____
__;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______
__。
70°,
40°
70°,40°或55°,55°
35°,
35°
想一想:
由刚才证明的△ABD≌
△ACD,除了能得到∠B=∠C
你还能发现什么?
A
B
D
C
等腰三角形的顶角平分线,底边上的中线,底边上的高相互重合.
性质2
(简写成“三线合一”)
∴BD=CD,∠ADB=∠ADC=90°.
A
B
C
D
1
2
证明:作顶角的平分线AD.
在△BAD和△CAD中,
AB=AC,
∠1=∠2,
AD=AD,
∴△BAD≌△CAD
(SAS)
根据等腰三角形的性质,
在△ABC中,AB=AC时,
(1)∵AD⊥BC,
∴∠
=∠
,
=
;
(2)∵AD是中线,
∴
⊥
,
∠
=∠
;
(3)∵AD是角平分线,
∴
⊥
,
=
。
A
B
C
D
BAD
CAD
BD
CD
BAD
CAD
AD
BC
AD
BC
BD
CD
练习2
1、等腰三角形的顶角一定是锐角。
2
、等腰三角形的底角一定是锐角。
3、等腰三角形的角平分线、中线和高互相重合。
(X)
(√)
(X)
等腰三角形的角平分线、中线和高,一定重合吗?
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,∠A=36°,∠ABC=∠C=72°
x
⌒
x
⌒
⌒
2x
例题:如图,在△ABC中
,AB=AC,点D在AC
上,且BD=BC=AD.
求△ABC各内角的度数?
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数
解:∵AB=AD=DC
∴
∠B=
∠ADB,∠C=
∠DAC
设
∠C=x,则
∠DAC=x,
∠B=
∠ADB=
∠C+
∠DAC=2x
在△ABC中,
∠B+
∠C+
∠BAD+
∠DAC
=2x+x+26°+x=180°
解得:x=38.5°,
∴
∠B=77°,
∠C=
38.5°
课本第77页练习第3题
谈谈你的收获!
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合
一”
学习的数学思想及方法:
分类讨论和一题多解。
解决等腰三角形问题时常用的辅助线
作业:
1.必做题:教科书81页第1、4、7题;
2.选做题:教科书83页第13题
结束寄语:
成功不是凭梦想和希望,而是凭努力和实践。
