2020-2021学年山东省菏泽市郓城县七年级上学期期中数学试卷 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省菏泽市郓城县七年级上学期期中数学试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 700.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 08:07:01 | ||
图片预览




文档简介
2020-2021学年山东省菏泽市郓城县七年级第一学期期中数学试卷
一、选择题(共8小题).
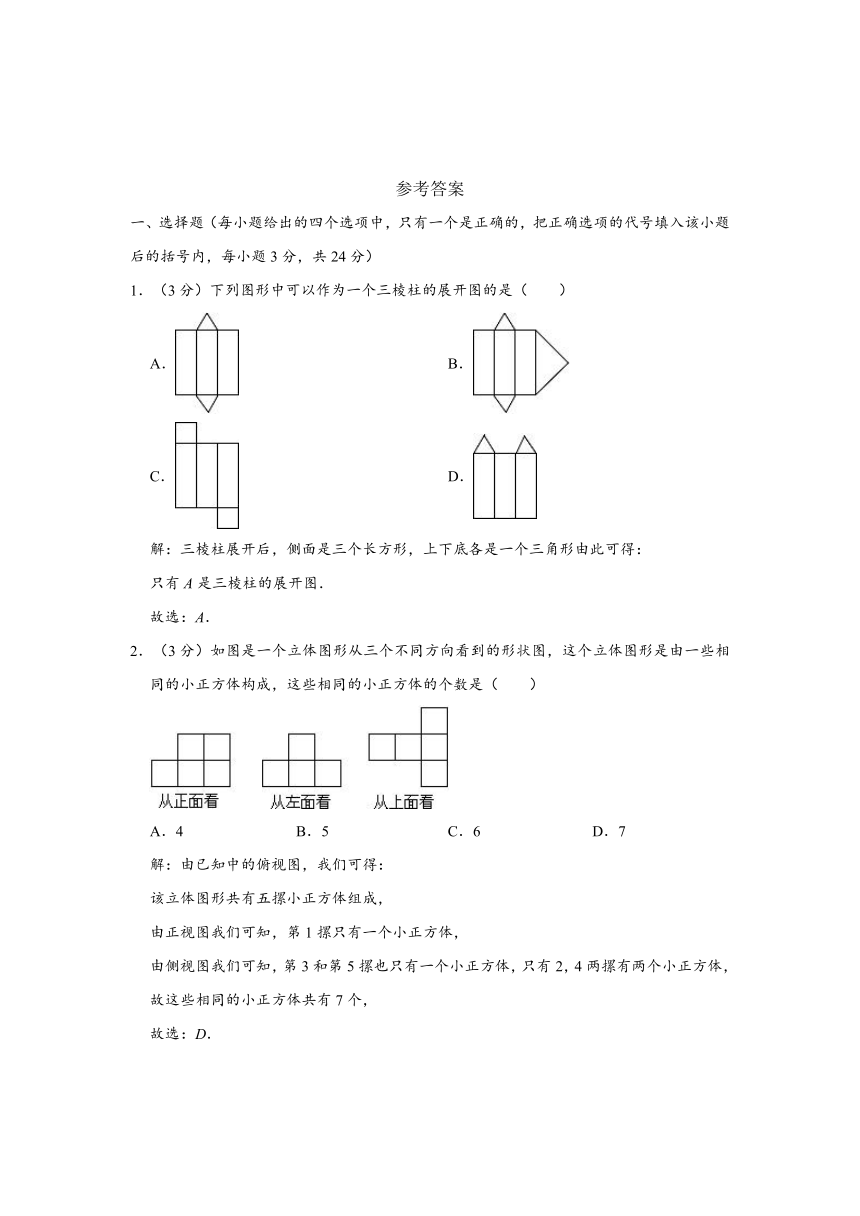
1.(3分)下列图形中可以作为一个三棱柱的展开图的是( )
A. B.
C. D.
2.(3分)如图是一个立体图形从三个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数是( )
A.4 B.5 C.6 D.7
3.(3分)有理数a,b在数轴上的位置如图所示,下面结论正确的( )
A.b﹣a<0 B.ab>0 C.a+b>0 D.|a|>|b|
4.(3分)数轴上点A、B表示的数分别是5、﹣3,它们之间的距离可以表示为( )
A.﹣3+5 B.﹣3﹣5 C.|﹣3+5| D.|﹣3﹣5|
5.(3分)国家提倡“低碳减排”,湛江某公司计划在海边建风能发电站,电站年均发电量约为213000000度,若将数据213000000用科学记数法表示为( )
A.213×106 B.21.3×107 C.2.13×108 D.2.13×109
6.(3分)今年,我校成功举办了“经典诵读”比赛,其中参加比赛的男同学有a人,女同学比男同学的少24人,则参加“经典诵读”比赛的学生一共有( )
A.(﹣24)人 B.(a﹣24)人
C.(a+24)人 D.(﹣24)人
7.(3分)若|x+y+2|+(xy﹣1)2=0,则(3x﹣xy+1)﹣(xy﹣3y﹣2)的值为( )
A.3 B.﹣3 C.﹣5 D.11
8.(3分)填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是( )
A.110 B.158 C.168 D.178
二、填空题(每小题3分,共18分)
9.(3分)夜晚的流星划过天空时留下一道明亮的光线,由此说明了 的数学事实.
10.(3分)用平面去截一个几何体,如果得出的是长方形,那么所截的这个几何体是 .
11.(3分)如果a与1互为相反数,则|a+2|等于 .
12.(3分)曾有微信用户提议应该补全朋友圈只有点赞功能的缺陷,增加“匿名点呸”的功能,如果将点32个赞记作+32,那么点2个呸时,应记作 .
13.(3分)已知多项式(M﹣1)x4﹣xN+2x﹣5是三次三项式,则(M+1)N= .
14.(3分)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大18,这样的两位数共有 个.
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)分别画出图中从三个方向看到的几何体的形状图.
16.(6分)若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.
17.(8分)一个圆柱的底面半径是10cm,高是18cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你求出这个截面面积.
18.(8分)画出数轴,用数轴上的点表示下列各数,并用“<”将它们连接起来.
﹣5,2.5,﹣,0,3.
19.(8分)计算:
(1)(﹣8)﹣(﹣2);
(2);
(3);
(4)[(﹣3)2﹣(﹣5)2]÷(﹣2).
20.(8分)猕猴桃是陕西周至的一大特产,现有20筐猕猴桃,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值 (单位:千克) ﹣3 ﹣2 ﹣1.5 0 1 2.5
筐数 1 4 2 3 2 8
(1)20筐猕猴桃中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐猕猴桃总计超过或不足多少千克?
(3)若猕猴桃每千克售价5元,则这20筐猕猴桃可卖多少元?
21.(8分)老师在黑板上书写了一个正确的验算过程,随后用手掌捂住了一个二次三项式,形式如图:
(1)求所捂的二次三项式:
(2)若﹣x2+2x=1,求所捂二次三项式的值.
22.(8分)先化简,再求值:,其中x=3,y=6.
23.(8分)某公司的某种产品由一家商店代销,双方协议不论这种产品销售情况如何,该公司每月给商店a元代销费,同时商店每销售一件产品有b元提成,该商店一月份销售了m件,二月份销售了n件.
(1)用式子表示这两个月公司应付给商店的钱数;
(2)假设代销费为每月200元,每件产品的提成为2元,该商店一月份销售了200件,二月份销售了250件,求该商店这两个月销售此种产品的收益.
24.(10分)观察下列等式:
第1个等式:a1==×(1﹣);
第2个等式:a2==×(﹣);
第3个等式:a3==×(﹣);
第4个等式:a4==×(﹣);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
参考答案
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填入该小题后的括号内,每小题3分,共24分)
1.(3分)下列图形中可以作为一个三棱柱的展开图的是( )
A. B.
C. D.
解:三棱柱展开后,侧面是三个长方形,上下底各是一个三角形由此可得:
只有A是三棱柱的展开图.
故选:A.
2.(3分)如图是一个立体图形从三个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数是( )
A.4 B.5 C.6 D.7
解:由已知中的俯视图,我们可得:
该立体图形共有五摞小正方体组成,
由正视图我们可知,第1摞只有一个小正方体,
由侧视图我们可知,第3和第5摞也只有一个小正方体,只有2,4两摞有两个小正方体,
故这些相同的小正方体共有7个,
故选:D.
3.(3分)有理数a,b在数轴上的位置如图所示,下面结论正确的( )
A.b﹣a<0 B.ab>0 C.a+b>0 D.|a|>|b|
解:根据点在数轴的位置,知:b<0<a,且|b|>|a|.
A、∵b<a,∴b﹣a<0,故本选项正确;
B、∵a>0,b<0,∴ab<0,故本选项错误;
C、∵b<0<a,且|b|>|a|,∴a+b<0,故本选项错误;
D、|b|>|a|,故本选项错误.
故选:A.
4.(3分)数轴上点A、B表示的数分别是5、﹣3,它们之间的距离可以表示为( )
A.﹣3+5 B.﹣3﹣5 C.|﹣3+5| D.|﹣3﹣5|
解:∵点A、B表示的数分别是5、﹣3,
∴它们之间的距离=|﹣3﹣5|=8,
故选:D.
5.(3分)国家提倡“低碳减排”,湛江某公司计划在海边建风能发电站,电站年均发电量约为213000000度,若将数据213000000用科学记数法表示为( )
A.213×106 B.21.3×107 C.2.13×108 D.2.13×109
解:将213000000用科学记数法表示为2.13×108.
故选:C.
6.(3分)今年,我校成功举办了“经典诵读”比赛,其中参加比赛的男同学有a人,女同学比男同学的少24人,则参加“经典诵读”比赛的学生一共有( )
A.(﹣24)人 B.(a﹣24)人
C.(a+24)人 D.(﹣24)人
解:女同学人数:a﹣24,
所以一共有学生:a+a﹣24=a﹣24,
故选:D.
7.(3分)若|x+y+2|+(xy﹣1)2=0,则(3x﹣xy+1)﹣(xy﹣3y﹣2)的值为( )
A.3 B.﹣3 C.﹣5 D.11
解:由|x+y+2|+(xy﹣1)2=0,得
,解得.
(3x﹣xy+1)﹣(xy﹣3y﹣2)=3x﹣xy+1﹣xy+3y+2
=3x+3y﹣2xy+3,
当x=1,y=1时,原式=﹣3﹣3﹣2+3=﹣5,
故选:C.
8.(3分)填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是( )
A.110 B.158 C.168 D.178
解:根据排列规律,10下面的数是12,10右面的数是14,
∵8=2×4﹣0,22=4×6﹣2,44=6×8﹣4,
∴m=12×14﹣10=158.
故选:B.
二、填空题(每小题3分,共18分)
9.(3分)夜晚的流星划过天空时留下一道明亮的光线,由此说明了 点动成线 的数学事实.
解:夜晚的流星划过天空时留下一道明亮的光线,由此说明了点动成线,
故答案为:点动成线.
10.(3分)用平面去截一个几何体,如果得出的是长方形,那么所截的这个几何体是 棱柱,圆柱,棱锥 .
解:如果得出的是长方形,那么所截的这个几何体是棱柱,圆柱,棱锥.
11.(3分)如果a与1互为相反数,则|a+2|等于 1 .
解:∵a与1互为相反数,
∴a=﹣1,
把a=﹣1代入|a+2|得,
|a+2|=|﹣1+2|=1.
故答案为1.
12.(3分)曾有微信用户提议应该补全朋友圈只有点赞功能的缺陷,增加“匿名点呸”的功能,如果将点32个赞记作+32,那么点2个呸时,应记作 ﹣2 .
解:如果将点32个赞记作+32,那么点2个呸时,应记作﹣2.
故答案是:﹣2.
13.(3分)已知多项式(M﹣1)x4﹣xN+2x﹣5是三次三项式,则(M+1)N= 8 .
解:由题意可知:N=3,M﹣1=0,
∴M=1,N=3,
∴原式=23=8,
故答案为:8
14.(3分)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大18,这样的两位数共有 7 个.
解:设原来的两位数为10a+b,
根据题意可得:
10a+b+18=10b+a,
解得:a=b﹣2,
∵b可取从3到9的所有自然数,
即3、4、5、6、7、8、9,
∴这样的两位数共有7个,
它们分别是13,24,35,46,57,68,79.
故答案为:7.
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)分别画出图中从三个方向看到的几何体的形状图.
解:如图所示:
16.(6分)若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.
解:这是一个正方体的平面展开图,共有六个面,
其中面“z”与面“3”相对,面“y”与面“﹣2”相对,“x”与面“10”相对.
则z+3=5,y+(﹣2)=5,x+10=5,
解得z=2,y=7,x=﹣5.
故x+y+z=4.
17.(8分)一个圆柱的底面半径是10cm,高是18cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你求出这个截面面积.
解:(1)所得的截面是圆;
(2)所得的截面是长方形;
(3)当平面沿竖直方向且经过两个底面的圆心时,截得的长方形面积最大,
这时,长方形的一边等于圆柱的高,长方形的另一边等于圆柱的底面直径,
则这个长方形的面积为:10×2×18=360(cm2).
18.(8分)画出数轴,用数轴上的点表示下列各数,并用“<”将它们连接起来.
﹣5,2.5,﹣,0,3.
解:如图所示:
,
﹣5<﹣<0<2.5<3.
19.(8分)计算:
(1)(﹣8)﹣(﹣2);
(2);
(3);
(4)[(﹣3)2﹣(﹣5)2]÷(﹣2).
解:(1)(﹣8)﹣(﹣2)
=(﹣8)+2
=﹣6;
(2)
=+(﹣)
=+(﹣)
=;
(3)
=()×(﹣)×
=×(﹣)×
=﹣9;
(4)[(﹣3)2﹣(﹣5)2]÷(﹣2)
=(9﹣25)×(﹣)
=(﹣16)×(﹣)
=8.
20.(8分)猕猴桃是陕西周至的一大特产,现有20筐猕猴桃,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值 (单位:千克) ﹣3 ﹣2 ﹣1.5 0 1 2.5
筐数 1 4 2 3 2 8
(1)20筐猕猴桃中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐猕猴桃总计超过或不足多少千克?
(3)若猕猴桃每千克售价5元,则这20筐猕猴桃可卖多少元?
解:(1)2.5﹣(﹣3)=5.5(千克).
答:最重的一筐比最轻的一筐重5.5千克.
(2)1×(﹣3)+4×(﹣2)+2×(﹣1.5)+3×0+2×1+8×2.5=﹣3﹣8﹣3+2+20=8(千克).
答:20筐猕猴桃总计超过8千克.
(3)5×(25×20+8)=2540(元).
答:这20筐猕猴桃可卖2540元.
21.(8分)老师在黑板上书写了一个正确的验算过程,随后用手掌捂住了一个二次三项式,形式如图:
(1)求所捂的二次三项式:
(2)若﹣x2+2x=1,求所捂二次三项式的值.
解:(1)根据题意得:x2﹣5x+1+3x
=x2﹣2x+1;
(2)由﹣x2+2x=1,得到x2﹣2x=﹣1,
则原式=﹣1+1=0.
22.(8分)先化简,再求值:,其中x=3,y=6.
解:原式=x2﹣y+x﹣y2+x2+y2
=x2﹣y+x﹣y2,
当x=3,y=6时,原式=×9﹣×6+×3﹣×36=6﹣3+1﹣6=﹣2.
23.(8分)某公司的某种产品由一家商店代销,双方协议不论这种产品销售情况如何,该公司每月给商店a元代销费,同时商店每销售一件产品有b元提成,该商店一月份销售了m件,二月份销售了n件.
(1)用式子表示这两个月公司应付给商店的钱数;
(2)假设代销费为每月200元,每件产品的提成为2元,该商店一月份销售了200件,二月份销售了250件,求该商店这两个月销售此种产品的收益.
解:(1)表示这两个月公司应付给商店的钱数式子为:
a+mb+a+nb=2a+b(m+n);
(2)将a=200,b=2,m=200,n=250代入2a+b(m+n),
2×200+2×(200+250)=1300(元),
∴该商店这两个月销售此种产品的收益为1300元;
24.(10分)观察下列等式:
第1个等式:a1==×(1﹣);
第2个等式:a2==×(﹣);
第3个等式:a3==×(﹣);
第4个等式:a4==×(﹣);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
解:根据观察知答案分别为:
(1); ;
(2); ;
(3)a1+a2+a3+a4+…+a100
=×(1﹣)+×(﹣)+×(﹣)+×(﹣)+…+×
=(1﹣+﹣+﹣+﹣+…+﹣)
=(1﹣)
=×
=.
一、选择题(共8小题).
1.(3分)下列图形中可以作为一个三棱柱的展开图的是( )
A. B.
C. D.
2.(3分)如图是一个立体图形从三个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数是( )
A.4 B.5 C.6 D.7
3.(3分)有理数a,b在数轴上的位置如图所示,下面结论正确的( )
A.b﹣a<0 B.ab>0 C.a+b>0 D.|a|>|b|
4.(3分)数轴上点A、B表示的数分别是5、﹣3,它们之间的距离可以表示为( )
A.﹣3+5 B.﹣3﹣5 C.|﹣3+5| D.|﹣3﹣5|
5.(3分)国家提倡“低碳减排”,湛江某公司计划在海边建风能发电站,电站年均发电量约为213000000度,若将数据213000000用科学记数法表示为( )
A.213×106 B.21.3×107 C.2.13×108 D.2.13×109
6.(3分)今年,我校成功举办了“经典诵读”比赛,其中参加比赛的男同学有a人,女同学比男同学的少24人,则参加“经典诵读”比赛的学生一共有( )
A.(﹣24)人 B.(a﹣24)人
C.(a+24)人 D.(﹣24)人
7.(3分)若|x+y+2|+(xy﹣1)2=0,则(3x﹣xy+1)﹣(xy﹣3y﹣2)的值为( )
A.3 B.﹣3 C.﹣5 D.11
8.(3分)填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是( )
A.110 B.158 C.168 D.178
二、填空题(每小题3分,共18分)
9.(3分)夜晚的流星划过天空时留下一道明亮的光线,由此说明了 的数学事实.
10.(3分)用平面去截一个几何体,如果得出的是长方形,那么所截的这个几何体是 .
11.(3分)如果a与1互为相反数,则|a+2|等于 .
12.(3分)曾有微信用户提议应该补全朋友圈只有点赞功能的缺陷,增加“匿名点呸”的功能,如果将点32个赞记作+32,那么点2个呸时,应记作 .
13.(3分)已知多项式(M﹣1)x4﹣xN+2x﹣5是三次三项式,则(M+1)N= .
14.(3分)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大18,这样的两位数共有 个.
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)分别画出图中从三个方向看到的几何体的形状图.
16.(6分)若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.
17.(8分)一个圆柱的底面半径是10cm,高是18cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你求出这个截面面积.
18.(8分)画出数轴,用数轴上的点表示下列各数,并用“<”将它们连接起来.
﹣5,2.5,﹣,0,3.
19.(8分)计算:
(1)(﹣8)﹣(﹣2);
(2);
(3);
(4)[(﹣3)2﹣(﹣5)2]÷(﹣2).
20.(8分)猕猴桃是陕西周至的一大特产,现有20筐猕猴桃,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值 (单位:千克) ﹣3 ﹣2 ﹣1.5 0 1 2.5
筐数 1 4 2 3 2 8
(1)20筐猕猴桃中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐猕猴桃总计超过或不足多少千克?
(3)若猕猴桃每千克售价5元,则这20筐猕猴桃可卖多少元?
21.(8分)老师在黑板上书写了一个正确的验算过程,随后用手掌捂住了一个二次三项式,形式如图:
(1)求所捂的二次三项式:
(2)若﹣x2+2x=1,求所捂二次三项式的值.
22.(8分)先化简,再求值:,其中x=3,y=6.
23.(8分)某公司的某种产品由一家商店代销,双方协议不论这种产品销售情况如何,该公司每月给商店a元代销费,同时商店每销售一件产品有b元提成,该商店一月份销售了m件,二月份销售了n件.
(1)用式子表示这两个月公司应付给商店的钱数;
(2)假设代销费为每月200元,每件产品的提成为2元,该商店一月份销售了200件,二月份销售了250件,求该商店这两个月销售此种产品的收益.
24.(10分)观察下列等式:
第1个等式:a1==×(1﹣);
第2个等式:a2==×(﹣);
第3个等式:a3==×(﹣);
第4个等式:a4==×(﹣);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
参考答案
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填入该小题后的括号内,每小题3分,共24分)
1.(3分)下列图形中可以作为一个三棱柱的展开图的是( )
A. B.
C. D.
解:三棱柱展开后,侧面是三个长方形,上下底各是一个三角形由此可得:
只有A是三棱柱的展开图.
故选:A.
2.(3分)如图是一个立体图形从三个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数是( )
A.4 B.5 C.6 D.7
解:由已知中的俯视图,我们可得:
该立体图形共有五摞小正方体组成,
由正视图我们可知,第1摞只有一个小正方体,
由侧视图我们可知,第3和第5摞也只有一个小正方体,只有2,4两摞有两个小正方体,
故这些相同的小正方体共有7个,
故选:D.
3.(3分)有理数a,b在数轴上的位置如图所示,下面结论正确的( )
A.b﹣a<0 B.ab>0 C.a+b>0 D.|a|>|b|
解:根据点在数轴的位置,知:b<0<a,且|b|>|a|.
A、∵b<a,∴b﹣a<0,故本选项正确;
B、∵a>0,b<0,∴ab<0,故本选项错误;
C、∵b<0<a,且|b|>|a|,∴a+b<0,故本选项错误;
D、|b|>|a|,故本选项错误.
故选:A.
4.(3分)数轴上点A、B表示的数分别是5、﹣3,它们之间的距离可以表示为( )
A.﹣3+5 B.﹣3﹣5 C.|﹣3+5| D.|﹣3﹣5|
解:∵点A、B表示的数分别是5、﹣3,
∴它们之间的距离=|﹣3﹣5|=8,
故选:D.
5.(3分)国家提倡“低碳减排”,湛江某公司计划在海边建风能发电站,电站年均发电量约为213000000度,若将数据213000000用科学记数法表示为( )
A.213×106 B.21.3×107 C.2.13×108 D.2.13×109
解:将213000000用科学记数法表示为2.13×108.
故选:C.
6.(3分)今年,我校成功举办了“经典诵读”比赛,其中参加比赛的男同学有a人,女同学比男同学的少24人,则参加“经典诵读”比赛的学生一共有( )
A.(﹣24)人 B.(a﹣24)人
C.(a+24)人 D.(﹣24)人
解:女同学人数:a﹣24,
所以一共有学生:a+a﹣24=a﹣24,
故选:D.
7.(3分)若|x+y+2|+(xy﹣1)2=0,则(3x﹣xy+1)﹣(xy﹣3y﹣2)的值为( )
A.3 B.﹣3 C.﹣5 D.11
解:由|x+y+2|+(xy﹣1)2=0,得
,解得.
(3x﹣xy+1)﹣(xy﹣3y﹣2)=3x﹣xy+1﹣xy+3y+2
=3x+3y﹣2xy+3,
当x=1,y=1时,原式=﹣3﹣3﹣2+3=﹣5,
故选:C.
8.(3分)填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是( )
A.110 B.158 C.168 D.178
解:根据排列规律,10下面的数是12,10右面的数是14,
∵8=2×4﹣0,22=4×6﹣2,44=6×8﹣4,
∴m=12×14﹣10=158.
故选:B.
二、填空题(每小题3分,共18分)
9.(3分)夜晚的流星划过天空时留下一道明亮的光线,由此说明了 点动成线 的数学事实.
解:夜晚的流星划过天空时留下一道明亮的光线,由此说明了点动成线,
故答案为:点动成线.
10.(3分)用平面去截一个几何体,如果得出的是长方形,那么所截的这个几何体是 棱柱,圆柱,棱锥 .
解:如果得出的是长方形,那么所截的这个几何体是棱柱,圆柱,棱锥.
11.(3分)如果a与1互为相反数,则|a+2|等于 1 .
解:∵a与1互为相反数,
∴a=﹣1,
把a=﹣1代入|a+2|得,
|a+2|=|﹣1+2|=1.
故答案为1.
12.(3分)曾有微信用户提议应该补全朋友圈只有点赞功能的缺陷,增加“匿名点呸”的功能,如果将点32个赞记作+32,那么点2个呸时,应记作 ﹣2 .
解:如果将点32个赞记作+32,那么点2个呸时,应记作﹣2.
故答案是:﹣2.
13.(3分)已知多项式(M﹣1)x4﹣xN+2x﹣5是三次三项式,则(M+1)N= 8 .
解:由题意可知:N=3,M﹣1=0,
∴M=1,N=3,
∴原式=23=8,
故答案为:8
14.(3分)一个两位数,若交换其个位数与十位数的位置,则所得新两位数比原两位数大18,这样的两位数共有 7 个.
解:设原来的两位数为10a+b,
根据题意可得:
10a+b+18=10b+a,
解得:a=b﹣2,
∵b可取从3到9的所有自然数,
即3、4、5、6、7、8、9,
∴这样的两位数共有7个,
它们分别是13,24,35,46,57,68,79.
故答案为:7.
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)分别画出图中从三个方向看到的几何体的形状图.
解:如图所示:
16.(6分)若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.
解:这是一个正方体的平面展开图,共有六个面,
其中面“z”与面“3”相对,面“y”与面“﹣2”相对,“x”与面“10”相对.
则z+3=5,y+(﹣2)=5,x+10=5,
解得z=2,y=7,x=﹣5.
故x+y+z=4.
17.(8分)一个圆柱的底面半径是10cm,高是18cm,把这个圆柱放在水平桌面上,如图所示.
(1)如果用一个平面沿水平方向去截这个圆柱,所得的截面是什么形状?
(2)如果用一个平面沿竖直方向去截这个圆柱,所得的截面是什么形状?
(3)怎样截时所得的截面是长方形且长方形的面积最大,请你求出这个截面面积.
解:(1)所得的截面是圆;
(2)所得的截面是长方形;
(3)当平面沿竖直方向且经过两个底面的圆心时,截得的长方形面积最大,
这时,长方形的一边等于圆柱的高,长方形的另一边等于圆柱的底面直径,
则这个长方形的面积为:10×2×18=360(cm2).
18.(8分)画出数轴,用数轴上的点表示下列各数,并用“<”将它们连接起来.
﹣5,2.5,﹣,0,3.
解:如图所示:
,
﹣5<﹣<0<2.5<3.
19.(8分)计算:
(1)(﹣8)﹣(﹣2);
(2);
(3);
(4)[(﹣3)2﹣(﹣5)2]÷(﹣2).
解:(1)(﹣8)﹣(﹣2)
=(﹣8)+2
=﹣6;
(2)
=+(﹣)
=+(﹣)
=;
(3)
=()×(﹣)×
=×(﹣)×
=﹣9;
(4)[(﹣3)2﹣(﹣5)2]÷(﹣2)
=(9﹣25)×(﹣)
=(﹣16)×(﹣)
=8.
20.(8分)猕猴桃是陕西周至的一大特产,现有20筐猕猴桃,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值 (单位:千克) ﹣3 ﹣2 ﹣1.5 0 1 2.5
筐数 1 4 2 3 2 8
(1)20筐猕猴桃中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐猕猴桃总计超过或不足多少千克?
(3)若猕猴桃每千克售价5元,则这20筐猕猴桃可卖多少元?
解:(1)2.5﹣(﹣3)=5.5(千克).
答:最重的一筐比最轻的一筐重5.5千克.
(2)1×(﹣3)+4×(﹣2)+2×(﹣1.5)+3×0+2×1+8×2.5=﹣3﹣8﹣3+2+20=8(千克).
答:20筐猕猴桃总计超过8千克.
(3)5×(25×20+8)=2540(元).
答:这20筐猕猴桃可卖2540元.
21.(8分)老师在黑板上书写了一个正确的验算过程,随后用手掌捂住了一个二次三项式,形式如图:
(1)求所捂的二次三项式:
(2)若﹣x2+2x=1,求所捂二次三项式的值.
解:(1)根据题意得:x2﹣5x+1+3x
=x2﹣2x+1;
(2)由﹣x2+2x=1,得到x2﹣2x=﹣1,
则原式=﹣1+1=0.
22.(8分)先化简,再求值:,其中x=3,y=6.
解:原式=x2﹣y+x﹣y2+x2+y2
=x2﹣y+x﹣y2,
当x=3,y=6时,原式=×9﹣×6+×3﹣×36=6﹣3+1﹣6=﹣2.
23.(8分)某公司的某种产品由一家商店代销,双方协议不论这种产品销售情况如何,该公司每月给商店a元代销费,同时商店每销售一件产品有b元提成,该商店一月份销售了m件,二月份销售了n件.
(1)用式子表示这两个月公司应付给商店的钱数;
(2)假设代销费为每月200元,每件产品的提成为2元,该商店一月份销售了200件,二月份销售了250件,求该商店这两个月销售此种产品的收益.
解:(1)表示这两个月公司应付给商店的钱数式子为:
a+mb+a+nb=2a+b(m+n);
(2)将a=200,b=2,m=200,n=250代入2a+b(m+n),
2×200+2×(200+250)=1300(元),
∴该商店这两个月销售此种产品的收益为1300元;
24.(10分)观察下列等式:
第1个等式:a1==×(1﹣);
第2个等式:a2==×(﹣);
第3个等式:a3==×(﹣);
第4个等式:a4==×(﹣);
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+a4+…+a100的值.
解:根据观察知答案分别为:
(1); ;
(2); ;
(3)a1+a2+a3+a4+…+a100
=×(1﹣)+×(﹣)+×(﹣)+×(﹣)+…+×
=(1﹣+﹣+﹣+﹣+…+﹣)
=(1﹣)
=×
=.
同课章节目录
