人教版(2019)必修2《第6章 圆周运动》2020年单元测试卷
文档属性
| 名称 | 人教版(2019)必修2《第6章 圆周运动》2020年单元测试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 120.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-30 10:15:43 | ||
图片预览




文档简介
人教版(2019)必修2《第6章圆周运动》
2020年单元测试卷
如图所示,一个小球沿光滑的漏斗壁在某一水平面内做匀速圆周运动,关于小球的受力情况,下列说法正确的是
A.
只受重力和支持力
B.
受重力、支持力和压力
C.
受重力、支持力和向心力
D.
受重力、压力和向心力
关于曲线运动,以下说法中正确的是
A.
平抛运动是一种匀变速运动
B.
物体在恒力作用下不可能做曲线运动
C.
做匀速圆周运动的物体,所受合力是恒定的
D.
做圆周运动的物体合力总是与速度方向垂直
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为点在小轮上,到小轮中心的距离为点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑,则
A.
a点与b点的线速度大小相等
B.
a点与b点的向心加速度大小相等
C.
a点与c点的线速度大小相等
D.
a点与d点的向心加速度大小相等
下列一些说法中不正确的有
A.
产生离心现象的原理有时可利用为人类服务
B.
汽车转弯时要利用离心现象防止事故
C.
洗衣机脱水桶脱干衣服,脱水桶的转速不能太小
D.
汽车转弯时要防止离心现象的发生,避免事故发生
在高速公路的拐弯处,通常路面都是外高内低。如图所示,在某路段汽车向左拐弯,司机左侧的路面比右侧的路面低一些。汽车的运动可看作是做半径为R的在水平面内的圆周运动。设内外路面高度差为h,路基的水平宽度为d,路面的宽度为已知重力加速度为g。要使车轮与路面之间的横向摩擦力即垂直于前进方向等于零,则汽车转弯时的车速应等于
A.
B.
C.
D.
如图所示,杂技演员表演水流星节目.一根长为L的细绳两端系着盛水的杯子,演员握住绳中间,随着演员的抡动,杯子在竖直平面内做圆周运动,杯子运动中水始终不会从杯子洒出,设重力加速度为g,则杯子运动到最高点的角速度至少为
A.
B.
C.
D.
如图所示,质量为m的小环套在半径为R的圆形环上,在竖直平面内做圆周运动,设小环在最高点的速度为v,则
A.
B.
C.
当,小环压轨道内侧
D.
当,小环压轨道外侧
如图所示,A、B、C三个物体放在旋转圆台上,动摩擦因数均为可认为最大静摩擦力和滑动摩擦力相等,A质量为2m,B、C的质量均为m,A、B离轴距离为R,C离轴距离为2R,则当圆台旋转时,若A、B、C均没有滑动,则
A.
C的向心加速度最大
B.
B的摩擦力最小
C.
当圆台转速增大时,B比A先滑动
D.
圆台转速增大时,C比B先滑动
小球m用长为L的悬线固定在O点,在O点正下方处有一光滑圆钉如图所示今把小球拉到悬线呈水平后无初速地释放,当悬线竖直状态且与钉相碰时
A.
小球的速度突然增大
B.
小球的向心加速度突然增大
C.
小球的向心加速度不变
D.
悬线的拉力突然增大
如图所示,细杆的一端与一小球相连,可绕过O点的水平轴自由转动.现给小球一初速度,使它做圆周运动,图中a、b分别表示小球轨道的最低点和最高点,则关于杆对球的作用力的说法正确的是
A.
a处一定为拉力
B.
a处一定为推力
C.
b处一定为拉力
D.
b处一定为推力
如图所示,质量为m的物体从半径为R的半球形碗边向碗底滑动,滑到最低点时的速度为v,若物体与碗的动摩擦因数为,则物体滑到最低点时受到的摩擦力是
A.
B.
C.
D.
半径为R的光滑半圆球固定在水平面上,顶部有一小物体m,如图所示,今给小物体一个水平初速度,则物体将
A.
沿球面滑至m点
B.
先沿球面滑至某点N再离开球面做斜下抛运动
C.
按半径大于R的新圆弧轨道运动
D.
立即离开半球面作平抛运动
A、B两球质量分别为与,用一劲度系数为K的弹簧相连,一长为的细线与相连,置于水平光滑桌面上,细线的另一端拴在竖直轴上,如图所示,当与均以角速度绕做匀速圆周运动时,弹簧长度为.
求:此时弹簧伸长量多大?绳子张力多大?
将线突然烧断瞬间两球加速度各多大?
一架滑翔机以的速率,沿着半径为1200m的水平圆弧飞行。g取,求机翼和水平面间夹角的正切值。
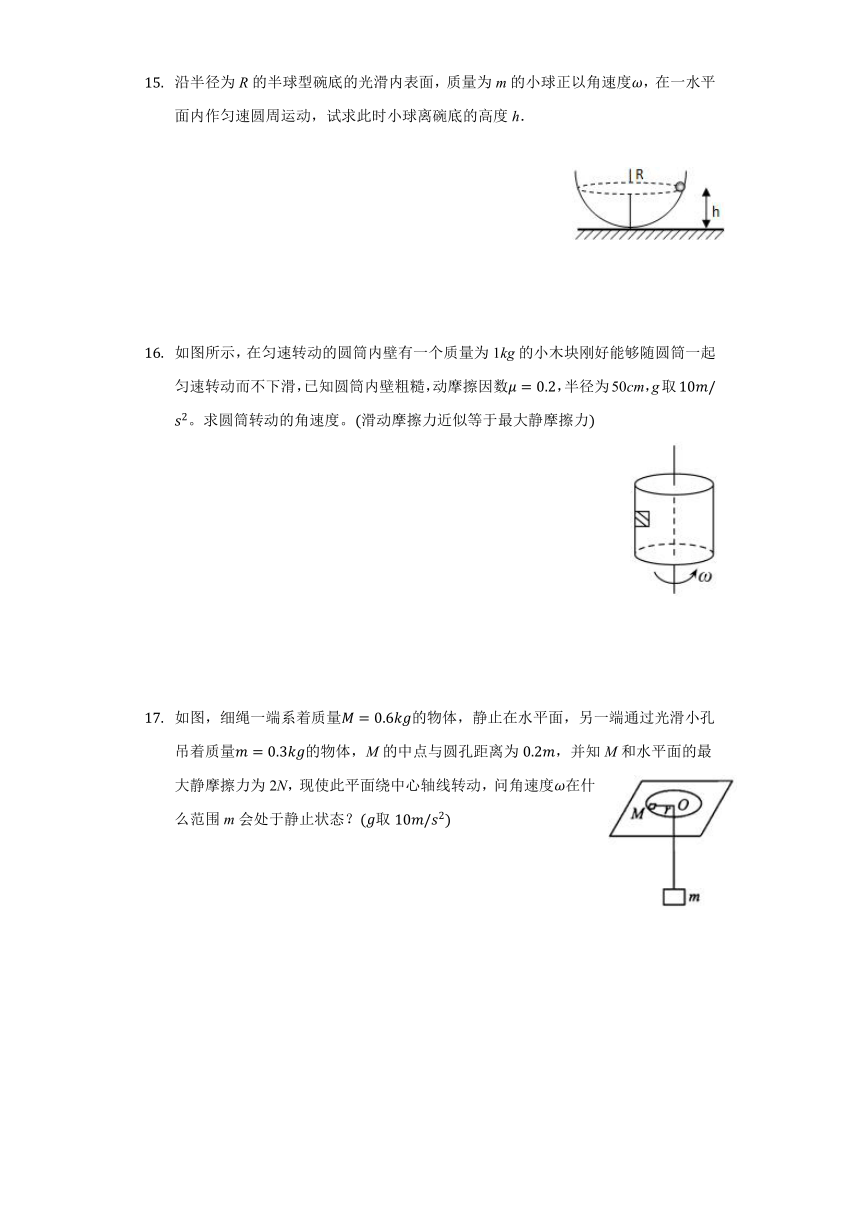
沿半径为R的半球型碗底的光滑内表面,质量为m的小球正以角速度,在一水平面内作匀速圆周运动,试求此时小球离碗底的高度h.
如图所示,在匀速转动的圆筒内壁有一个质量为1kg的小木块刚好能够随圆筒一起匀速转动而不下滑,已知圆筒内壁粗糙,动摩擦因数,半径为50cm,g取。求圆筒转动的角速度。滑动摩擦力近似等于最大静摩擦力
如图,细绳一端系着质量的物体,静止在水平面,另一端通过光滑小孔吊着质量的物体,M的中点与圆孔距离为,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度在什么范围m会处于静止状态?取
答案和解析
1.【答案】A
【解析】解:小球只受重力和支持力两个力的作用,靠两个力的合力提供向心力,向心力不是物体实际受到的力,是做圆周运动所需要的力,靠其它力提供。故A正确,BCD错误。
故选:A。
小球受重力和支持力,由两个力的合力提供小球做圆周运动的向心力。
本题是圆锥摆类型的问题,分析受力情况,确定小球向心力的来源,再由牛顿第二定律和圆周运动结合进行分析,是常用的方法和思路。
2.【答案】A
【解析】解:A、平抛运动只受到重力的作用,是一种加速度不变的曲线运动,即匀变速曲线运动,故A正确;
B、物体做曲线运动的条件是合力与速度不在同一条直线上,物体在恒力作用下,可以做曲线运动,比如平抛运动,所以B错误。
C、匀速圆周运动的向心力的方向始终是指向圆心的,方向是不断变化的,所以匀速圆周运动一定是受到变力的作用,所以C错误。
D、物体做匀速圆周运动的物体合力才总是与速度方向垂直,所以D错误。
故选:A。
物体做曲线运动的条件是合力与速度不在同一条直线上,合外力大小和方向不一定变化,由此可以分析得出结论.
本题关键是对质点做曲线运动的条件的考查,匀速圆周运动,平抛运动等都是曲线运动,对于它们的特点要掌握住.
3.【答案】CD
【解析】解:A、a、c两点靠传送带传动,线速度大小相等,b、c两点共轴转动,角速度相等,c、b的半径之比为2;1,根据知,c、b的线速度之比为2:1,所以a、b的线速度之比为2:1,故A错误,C正确.
B、根据知,a、c的向心加速度之比为2:1,根据知,c、b的向心加速度之比为2:1,所以a、b两点的向心加速度之比4:1,故B错误.
D、a、c两点的向心加速度之比为2:1,根据知,c、d两点的向心加速度之比为1;2,所以a、d两点的向心加速度大小相等,故D正确.
故选:CD.
共轴转动的各点角速度相等,靠传送带传动轮子上的点线速度大小相等,根据,求出各点线速度、角速度和向心加速度的大小.
解决本题的关键知道线速度、角速度、向心加速度与半径的关系,以及知道共轴转动的各点角速度相等,靠传送带传动轮子上的点线速度大小相等.
4.【答案】B
【解析】解:A、产生离心现象的原理有时可利用为人类服务,比如洗衣机脱水桶脱干衣服。故A正确;
B、因为,所以速度越快所需的向心力就越大,汽车转弯时要限制速度,来减小汽车所需的向心力,防止离心运动。故B错误,D正确;
C、洗衣机脱水工作就是应用了水的离心运动。故C正确。
本题选择错误的,故选:B。
做圆周运动的物体,在受到指向圆心的合外力突然消失,或者不足以提供圆周运动所需的向心力的情况下,就做逐渐远离圆心的运动,这种运动叫做离心运动.所有远离圆心的运动都是离心运动,但不一定沿切线方向飞出.
物体做离心运动的条件:合外力突然消失或者不足以提供圆周运动所需的向心力.注意所有远离圆心的运动都是离心运动,但不一定沿切线方向飞出.
5.【答案】B
【解析】解:设路面的倾角为,作出汽车的受力图,如图
根据牛顿第二定律,得
??
又由数学知识得到
??
联立解得
??
故选:B。
要使车轮与路面之间的横向摩擦力等于零,则汽车转弯时,由路面的支持力与重力的合力提供汽车的向心力,根据牛顿第二定律,结合数学知识求解车速。
本题是生活中圆周运动的问题,关键是分析物体的受力情况,确定向心力的来源。
6.【答案】B
【解析】解:据题知,杯子圆周运动的半径
杯子运动到最高点时,水恰好不流出,由水的重力刚好提供其做圆周运动的向心力,根据牛顿第二定律得:
解得:
故选:B。
杯子运动到最高点时,水恰好不流出时,由水的重力刚好提供其做圆周运动的向心力,根据牛顿第二定律求解最小角速度.
本题应用牛顿第二定律破解水流星节目成功的奥秘,关键在于分析受力情况,确定向心力的来源.
7.【答案】BCD
【解析】解:AB、小环套在光滑大圆环轨道上做圆周运动,在最高点时,大环可以对小环产生向下的压力,也可以产生向上的压力,也可以没有作用力。当小环与大环之间没有作用力时,只有小环的重力提供向心力,即,得;在最高点时,若大环对小环产生向上的压力,即小环压轨道外侧,则有,解得;在最高点时,若大环对小环产生向下的压力,即小环压轨道内侧,则有,解得;故A错误,B正确;
CD、在最高点时,若大环对小环产生向上的压力,即小环压轨道外侧,则有,解得;在最高点时,若大环对小环产生向下的压力,即小环压轨道内侧,则有,解得;故CD正确。
故选:BCD。
小环经过圆环最高点时,小环套在光滑大圆环轨道上,故大环可以对小环产生向下的压力,也可以产生向上的压力,也可以没有作用力;当大环对小球的弹力为零,靠重力提供向心力,根据牛顿第二定律求出小球的速度,此时向心加速度为重力加速度。
本题要注意,小环套在大环上,不是小球在轨道内侧的运动,临界条件不一样。大环可以对小环产生向下的压力,也可以产生向上的压力,也可以没有作用力,结合牛顿第二定律进行求解。
8.【答案】ABD
【解析】解:A、物体绕轴做匀速圆周运动,角速度相等,有,由于C物体的转动半径最大,故加速度最大,故A正确;
B、物体绕轴做匀速圆周运动,角速度相等,静摩擦力提供向心力,根据牛顿第二定律,有
,故B的摩擦力最小,故B正确;
C、D、物体恰好滑动时,静摩擦力达到最大,有
解得:
,即转动半径最大的最容易滑动,故物体C先滑动,然后物体A、B一起滑动,故C错误,D正确;
故选:ABD.
物体绕轴做匀速圆周运动,角速度相等,根据向心加速度公式分析加速度大小;根据静摩擦力提供向心力,根据牛顿第二定律列式求解即可.
本题关键是建立滑块做圆周运动的模型,根据牛顿第二定律列式求解出一般表达式进行分析,注意明确解题的关键在于三个物体的角速度均相同.
9.【答案】BD
【解析】解:A、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变,故A错误;
B、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变,但圆周运动的半径减小,向心加速度变大,故B正确;
C、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变,但圆周运动的半径减小,向心加速度变大,故C错误;
D、根据牛顿第二定律,有:,故绳子的拉力;
因R变小,故有钉子时,绳子上的拉力变大,故D正确;
故选:BD。
由机械能守恒可知小球到达最低点的速度,小球碰到钉子后仍做圆周运动,由向心力公式可得出绳子的拉力与小球转动半径的关系;由圆周运动的性质可知其线速度、角速度及向心加速度的大小关系.
本题中要注意细绳碰到钉子前后转动半径的变化,再由向心力公式分析绳子上的拉力变化.
10.【答案】A
【解析】解:A、过最低点a时,小球做圆周运动,需要的向心力竖直向上,指向圆心。
根据最低点小球的合力提供向心力,那么小球只有受竖直向下的重力和竖直向上的拉力。故A正确,B错误。
C、过最点b时,小球做圆周运动,需要的向心力竖直向下,指向圆心。
由于轻杆能对小球可以提供支持力,也可以提供拉力,
当在b点时速度时,小球的重力大于其所需的向心力,轻杆对小球有竖直向上的支持力,
当在b点时速度时,小球的重力等于其所需的向心力,轻杆对小球的作用力为0。
当在b点时速度时,小球的重力不足以提供向心力,轻杆对小球有指向圆心的拉力。
故C、D错误。
故选:A。
对小球在a、b点进行受力分析,由于小球做圆周运动,小球需要向心力.
找出小球向心力的来源,根据牛顿第二定律列出等式,判断杆对球的作用力的方向.
轻杆的作用力可以提供支持力,也可以提供拉力,
要判断是拉力还是支持力,我们要从小球所需要得向心力入手研究,根据需要的向心力的大小和方向确定杆子的作用力.
11.【答案】B
【解析】解:滑块经过碗底时,由重力和支持力的合力提供向心力,根据牛顿第二定律得:
则碗底对球支持力为:
所以在过碗底时滑块受到摩擦力的大小为:
故选:B。
滑块经过碗底时,由重力和碗底对球支持力的合力提供向心力,根据牛顿第二定律求出碗底对球的支持力,再由摩擦力公式求解在过碗底时滑块受到摩擦力的大小.
本题运用牛顿第二定律研究圆周运动物体受力情况,关键确定向心力的来源,比较基本,不能失分.
12.【答案】D
【解析】解:在最高点,有,,所以知物块在最高点仅受重力,有水平初速度,所以物块离开半球面做平抛运动.故D正确,A、B、C错误.
故选D.
物块在半圆球的最高点,沿半径方向的合力提供向心力,求出支持力的大小,从而判断出物块的运动情况.
解决本题的关键知道圆周运动径向的合力提供向心力.以及知道仅受重力,有水平初速度将做平抛运动.
13.【答案】解:对B球有:,
又根据胡克定律得:
所以
对A球有:
所以
故弹簧的伸长量为,绳子的张力为.
烧断细绳的瞬间,拉力,弹力F不变
根据牛顿第二定律,对A球有:
对B球有:
细绳烧断的瞬间两球的加速度分别为:,.
【解析】球绕做匀速圆周运动,靠弹簧的弹力提供向心力,求出弹簧的弹力,根据胡克定律即可得出弹簧的伸长量.A球在水平方向上受绳子的拉力和弹簧的弹力,两个力合力提供A球做圆周运动的向心力,从而求出绳子的拉力.
绳子突然烧断的瞬间,绳子拉力立即消失,弹簧的弹力来不及发生变化,根据牛顿第二定律分别求出两球的合力,从而得出两球的加速度.
解决本题的关键知道匀速圆周运动的向心力靠合力提供,以及知道在烧断细绳的瞬间,拉力立即消失,弹簧的弹力来不及改变,烧断细绳的前后瞬间弹力不变.
14.【答案】解:对滑翔机受力分析,如图所示:
设滑翔机的升力垂直机翼,机翼与水平方向的夹角为,
根据牛顿第二定律得:
解得机翼和水平面间夹角的正切值为:
答:机翼和水平面间夹角的正切值为。
【解析】滑翔机在水平面做匀速圆周运动,合力提供向心力,根据牛顿第二定律提供向心力即可求出机翼和水平面间夹角的正切值。
解决本题的关键理清滑翔机的运动情况,即水平面做圆周运动,根据牛顿第二定律求解。
15.【答案】解:小球靠重力和支持力的合力提供向心力,小球做圆周运动的半径为,根据力图可知,解得,所以。
答:此时小球离碗底的高度h为。
【解析】小球在光滑碗内靠重力和支持力的合力提供向心力,根据向心力和重力的关系求出小球与半球形碗球心连线与竖直方向的夹角,根据几何关系求出平面离碗底的距离h。
解决本题的关键知道小球做圆周运动向心力的来源,运用牛顿第二定律和几何关系进行求解。
16.【答案】解:小木块在竖直方向上受到的摩擦力与重力是一对平衡力,所以有:
根据滑动摩擦力公式:
联立解得:?N
小木块随圆周运动的向心力由圆筒内壁对木块的支持力提供,
根据牛顿第二定律得:
代入数据解得圆筒转动的角速度为:?
答:圆筒转动的角速度为。
【解析】物体在竖直方向受到重力与摩擦力,二者是平衡力,由摩擦力的公式即可求出弹力,由弹力提供向心力的公式即可求出。
本题考查了匀速圆周运动问题,解决此题得关键是要明确物体在圆筒内壁做匀速圆周运动,向心力是由筒壁对物体的支持力提供的。
17.【答案】解:设物体M和水平面保持相对静止。
当具有最小值时,M有向圆心运动趋势,故水平面对M的静摩擦力方向和指向圆心方向相反,且等于最大静摩擦力2N。
根据牛顿第二定律隔离M有:
??
?????解得
当具有最大值时,M有离开圆心趋势,水平面对M摩擦力方向指向圆心,大小也为2N。
再隔离M有:
??
??????
解得
所以范围是:
答:角速度在范围m会处于静止状态。
【解析】当角速度最小时,由于细绳的拉力作用,M有向圆心运动趋势,静摩擦力方向和指向圆心方向相反,并且达到最大值,由最大静摩擦力与细绳拉力的合力提供M的向心力。当角速度最大时,M有离开圆心趋势,静摩擦力方向指向圆心方向,并且达到最大值,由最大静摩擦力与细绳拉力的合力提供M的向心力。根据牛顿第二定律求解角速度及其范围。
本题考查应用牛顿定律处理临界问题的能力。当物体将滑动时,静摩擦力达到最大值。
第8页,共12页
2020年单元测试卷
如图所示,一个小球沿光滑的漏斗壁在某一水平面内做匀速圆周运动,关于小球的受力情况,下列说法正确的是
A.
只受重力和支持力
B.
受重力、支持力和压力
C.
受重力、支持力和向心力
D.
受重力、压力和向心力
关于曲线运动,以下说法中正确的是
A.
平抛运动是一种匀变速运动
B.
物体在恒力作用下不可能做曲线运动
C.
做匀速圆周运动的物体,所受合力是恒定的
D.
做圆周运动的物体合力总是与速度方向垂直
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为点在小轮上,到小轮中心的距离为点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑,则
A.
a点与b点的线速度大小相等
B.
a点与b点的向心加速度大小相等
C.
a点与c点的线速度大小相等
D.
a点与d点的向心加速度大小相等
下列一些说法中不正确的有
A.
产生离心现象的原理有时可利用为人类服务
B.
汽车转弯时要利用离心现象防止事故
C.
洗衣机脱水桶脱干衣服,脱水桶的转速不能太小
D.
汽车转弯时要防止离心现象的发生,避免事故发生
在高速公路的拐弯处,通常路面都是外高内低。如图所示,在某路段汽车向左拐弯,司机左侧的路面比右侧的路面低一些。汽车的运动可看作是做半径为R的在水平面内的圆周运动。设内外路面高度差为h,路基的水平宽度为d,路面的宽度为已知重力加速度为g。要使车轮与路面之间的横向摩擦力即垂直于前进方向等于零,则汽车转弯时的车速应等于
A.
B.
C.
D.
如图所示,杂技演员表演水流星节目.一根长为L的细绳两端系着盛水的杯子,演员握住绳中间,随着演员的抡动,杯子在竖直平面内做圆周运动,杯子运动中水始终不会从杯子洒出,设重力加速度为g,则杯子运动到最高点的角速度至少为
A.
B.
C.
D.
如图所示,质量为m的小环套在半径为R的圆形环上,在竖直平面内做圆周运动,设小环在最高点的速度为v,则
A.
B.
C.
当,小环压轨道内侧
D.
当,小环压轨道外侧
如图所示,A、B、C三个物体放在旋转圆台上,动摩擦因数均为可认为最大静摩擦力和滑动摩擦力相等,A质量为2m,B、C的质量均为m,A、B离轴距离为R,C离轴距离为2R,则当圆台旋转时,若A、B、C均没有滑动,则
A.
C的向心加速度最大
B.
B的摩擦力最小
C.
当圆台转速增大时,B比A先滑动
D.
圆台转速增大时,C比B先滑动
小球m用长为L的悬线固定在O点,在O点正下方处有一光滑圆钉如图所示今把小球拉到悬线呈水平后无初速地释放,当悬线竖直状态且与钉相碰时
A.
小球的速度突然增大
B.
小球的向心加速度突然增大
C.
小球的向心加速度不变
D.
悬线的拉力突然增大
如图所示,细杆的一端与一小球相连,可绕过O点的水平轴自由转动.现给小球一初速度,使它做圆周运动,图中a、b分别表示小球轨道的最低点和最高点,则关于杆对球的作用力的说法正确的是
A.
a处一定为拉力
B.
a处一定为推力
C.
b处一定为拉力
D.
b处一定为推力
如图所示,质量为m的物体从半径为R的半球形碗边向碗底滑动,滑到最低点时的速度为v,若物体与碗的动摩擦因数为,则物体滑到最低点时受到的摩擦力是
A.
B.
C.
D.
半径为R的光滑半圆球固定在水平面上,顶部有一小物体m,如图所示,今给小物体一个水平初速度,则物体将
A.
沿球面滑至m点
B.
先沿球面滑至某点N再离开球面做斜下抛运动
C.
按半径大于R的新圆弧轨道运动
D.
立即离开半球面作平抛运动
A、B两球质量分别为与,用一劲度系数为K的弹簧相连,一长为的细线与相连,置于水平光滑桌面上,细线的另一端拴在竖直轴上,如图所示,当与均以角速度绕做匀速圆周运动时,弹簧长度为.
求:此时弹簧伸长量多大?绳子张力多大?
将线突然烧断瞬间两球加速度各多大?
一架滑翔机以的速率,沿着半径为1200m的水平圆弧飞行。g取,求机翼和水平面间夹角的正切值。
沿半径为R的半球型碗底的光滑内表面,质量为m的小球正以角速度,在一水平面内作匀速圆周运动,试求此时小球离碗底的高度h.
如图所示,在匀速转动的圆筒内壁有一个质量为1kg的小木块刚好能够随圆筒一起匀速转动而不下滑,已知圆筒内壁粗糙,动摩擦因数,半径为50cm,g取。求圆筒转动的角速度。滑动摩擦力近似等于最大静摩擦力
如图,细绳一端系着质量的物体,静止在水平面,另一端通过光滑小孔吊着质量的物体,M的中点与圆孔距离为,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度在什么范围m会处于静止状态?取
答案和解析
1.【答案】A
【解析】解:小球只受重力和支持力两个力的作用,靠两个力的合力提供向心力,向心力不是物体实际受到的力,是做圆周运动所需要的力,靠其它力提供。故A正确,BCD错误。
故选:A。
小球受重力和支持力,由两个力的合力提供小球做圆周运动的向心力。
本题是圆锥摆类型的问题,分析受力情况,确定小球向心力的来源,再由牛顿第二定律和圆周运动结合进行分析,是常用的方法和思路。
2.【答案】A
【解析】解:A、平抛运动只受到重力的作用,是一种加速度不变的曲线运动,即匀变速曲线运动,故A正确;
B、物体做曲线运动的条件是合力与速度不在同一条直线上,物体在恒力作用下,可以做曲线运动,比如平抛运动,所以B错误。
C、匀速圆周运动的向心力的方向始终是指向圆心的,方向是不断变化的,所以匀速圆周运动一定是受到变力的作用,所以C错误。
D、物体做匀速圆周运动的物体合力才总是与速度方向垂直,所以D错误。
故选:A。
物体做曲线运动的条件是合力与速度不在同一条直线上,合外力大小和方向不一定变化,由此可以分析得出结论.
本题关键是对质点做曲线运动的条件的考查,匀速圆周运动,平抛运动等都是曲线运动,对于它们的特点要掌握住.
3.【答案】CD
【解析】解:A、a、c两点靠传送带传动,线速度大小相等,b、c两点共轴转动,角速度相等,c、b的半径之比为2;1,根据知,c、b的线速度之比为2:1,所以a、b的线速度之比为2:1,故A错误,C正确.
B、根据知,a、c的向心加速度之比为2:1,根据知,c、b的向心加速度之比为2:1,所以a、b两点的向心加速度之比4:1,故B错误.
D、a、c两点的向心加速度之比为2:1,根据知,c、d两点的向心加速度之比为1;2,所以a、d两点的向心加速度大小相等,故D正确.
故选:CD.
共轴转动的各点角速度相等,靠传送带传动轮子上的点线速度大小相等,根据,求出各点线速度、角速度和向心加速度的大小.
解决本题的关键知道线速度、角速度、向心加速度与半径的关系,以及知道共轴转动的各点角速度相等,靠传送带传动轮子上的点线速度大小相等.
4.【答案】B
【解析】解:A、产生离心现象的原理有时可利用为人类服务,比如洗衣机脱水桶脱干衣服。故A正确;
B、因为,所以速度越快所需的向心力就越大,汽车转弯时要限制速度,来减小汽车所需的向心力,防止离心运动。故B错误,D正确;
C、洗衣机脱水工作就是应用了水的离心运动。故C正确。
本题选择错误的,故选:B。
做圆周运动的物体,在受到指向圆心的合外力突然消失,或者不足以提供圆周运动所需的向心力的情况下,就做逐渐远离圆心的运动,这种运动叫做离心运动.所有远离圆心的运动都是离心运动,但不一定沿切线方向飞出.
物体做离心运动的条件:合外力突然消失或者不足以提供圆周运动所需的向心力.注意所有远离圆心的运动都是离心运动,但不一定沿切线方向飞出.
5.【答案】B
【解析】解:设路面的倾角为,作出汽车的受力图,如图
根据牛顿第二定律,得
??
又由数学知识得到
??
联立解得
??
故选:B。
要使车轮与路面之间的横向摩擦力等于零,则汽车转弯时,由路面的支持力与重力的合力提供汽车的向心力,根据牛顿第二定律,结合数学知识求解车速。
本题是生活中圆周运动的问题,关键是分析物体的受力情况,确定向心力的来源。
6.【答案】B
【解析】解:据题知,杯子圆周运动的半径
杯子运动到最高点时,水恰好不流出,由水的重力刚好提供其做圆周运动的向心力,根据牛顿第二定律得:
解得:
故选:B。
杯子运动到最高点时,水恰好不流出时,由水的重力刚好提供其做圆周运动的向心力,根据牛顿第二定律求解最小角速度.
本题应用牛顿第二定律破解水流星节目成功的奥秘,关键在于分析受力情况,确定向心力的来源.
7.【答案】BCD
【解析】解:AB、小环套在光滑大圆环轨道上做圆周运动,在最高点时,大环可以对小环产生向下的压力,也可以产生向上的压力,也可以没有作用力。当小环与大环之间没有作用力时,只有小环的重力提供向心力,即,得;在最高点时,若大环对小环产生向上的压力,即小环压轨道外侧,则有,解得;在最高点时,若大环对小环产生向下的压力,即小环压轨道内侧,则有,解得;故A错误,B正确;
CD、在最高点时,若大环对小环产生向上的压力,即小环压轨道外侧,则有,解得;在最高点时,若大环对小环产生向下的压力,即小环压轨道内侧,则有,解得;故CD正确。
故选:BCD。
小环经过圆环最高点时,小环套在光滑大圆环轨道上,故大环可以对小环产生向下的压力,也可以产生向上的压力,也可以没有作用力;当大环对小球的弹力为零,靠重力提供向心力,根据牛顿第二定律求出小球的速度,此时向心加速度为重力加速度。
本题要注意,小环套在大环上,不是小球在轨道内侧的运动,临界条件不一样。大环可以对小环产生向下的压力,也可以产生向上的压力,也可以没有作用力,结合牛顿第二定律进行求解。
8.【答案】ABD
【解析】解:A、物体绕轴做匀速圆周运动,角速度相等,有,由于C物体的转动半径最大,故加速度最大,故A正确;
B、物体绕轴做匀速圆周运动,角速度相等,静摩擦力提供向心力,根据牛顿第二定律,有
,故B的摩擦力最小,故B正确;
C、D、物体恰好滑动时,静摩擦力达到最大,有
解得:
,即转动半径最大的最容易滑动,故物体C先滑动,然后物体A、B一起滑动,故C错误,D正确;
故选:ABD.
物体绕轴做匀速圆周运动,角速度相等,根据向心加速度公式分析加速度大小;根据静摩擦力提供向心力,根据牛顿第二定律列式求解即可.
本题关键是建立滑块做圆周运动的模型,根据牛顿第二定律列式求解出一般表达式进行分析,注意明确解题的关键在于三个物体的角速度均相同.
9.【答案】BD
【解析】解:A、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变,故A错误;
B、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变,但圆周运动的半径减小,向心加速度变大,故B正确;
C、当悬线在竖直状态与钉相碰时根据能量守恒可知,小球速度不变,但圆周运动的半径减小,向心加速度变大,故C错误;
D、根据牛顿第二定律,有:,故绳子的拉力;
因R变小,故有钉子时,绳子上的拉力变大,故D正确;
故选:BD。
由机械能守恒可知小球到达最低点的速度,小球碰到钉子后仍做圆周运动,由向心力公式可得出绳子的拉力与小球转动半径的关系;由圆周运动的性质可知其线速度、角速度及向心加速度的大小关系.
本题中要注意细绳碰到钉子前后转动半径的变化,再由向心力公式分析绳子上的拉力变化.
10.【答案】A
【解析】解:A、过最低点a时,小球做圆周运动,需要的向心力竖直向上,指向圆心。
根据最低点小球的合力提供向心力,那么小球只有受竖直向下的重力和竖直向上的拉力。故A正确,B错误。
C、过最点b时,小球做圆周运动,需要的向心力竖直向下,指向圆心。
由于轻杆能对小球可以提供支持力,也可以提供拉力,
当在b点时速度时,小球的重力大于其所需的向心力,轻杆对小球有竖直向上的支持力,
当在b点时速度时,小球的重力等于其所需的向心力,轻杆对小球的作用力为0。
当在b点时速度时,小球的重力不足以提供向心力,轻杆对小球有指向圆心的拉力。
故C、D错误。
故选:A。
对小球在a、b点进行受力分析,由于小球做圆周运动,小球需要向心力.
找出小球向心力的来源,根据牛顿第二定律列出等式,判断杆对球的作用力的方向.
轻杆的作用力可以提供支持力,也可以提供拉力,
要判断是拉力还是支持力,我们要从小球所需要得向心力入手研究,根据需要的向心力的大小和方向确定杆子的作用力.
11.【答案】B
【解析】解:滑块经过碗底时,由重力和支持力的合力提供向心力,根据牛顿第二定律得:
则碗底对球支持力为:
所以在过碗底时滑块受到摩擦力的大小为:
故选:B。
滑块经过碗底时,由重力和碗底对球支持力的合力提供向心力,根据牛顿第二定律求出碗底对球的支持力,再由摩擦力公式求解在过碗底时滑块受到摩擦力的大小.
本题运用牛顿第二定律研究圆周运动物体受力情况,关键确定向心力的来源,比较基本,不能失分.
12.【答案】D
【解析】解:在最高点,有,,所以知物块在最高点仅受重力,有水平初速度,所以物块离开半球面做平抛运动.故D正确,A、B、C错误.
故选D.
物块在半圆球的最高点,沿半径方向的合力提供向心力,求出支持力的大小,从而判断出物块的运动情况.
解决本题的关键知道圆周运动径向的合力提供向心力.以及知道仅受重力,有水平初速度将做平抛运动.
13.【答案】解:对B球有:,
又根据胡克定律得:
所以
对A球有:
所以
故弹簧的伸长量为,绳子的张力为.
烧断细绳的瞬间,拉力,弹力F不变
根据牛顿第二定律,对A球有:
对B球有:
细绳烧断的瞬间两球的加速度分别为:,.
【解析】球绕做匀速圆周运动,靠弹簧的弹力提供向心力,求出弹簧的弹力,根据胡克定律即可得出弹簧的伸长量.A球在水平方向上受绳子的拉力和弹簧的弹力,两个力合力提供A球做圆周运动的向心力,从而求出绳子的拉力.
绳子突然烧断的瞬间,绳子拉力立即消失,弹簧的弹力来不及发生变化,根据牛顿第二定律分别求出两球的合力,从而得出两球的加速度.
解决本题的关键知道匀速圆周运动的向心力靠合力提供,以及知道在烧断细绳的瞬间,拉力立即消失,弹簧的弹力来不及改变,烧断细绳的前后瞬间弹力不变.
14.【答案】解:对滑翔机受力分析,如图所示:
设滑翔机的升力垂直机翼,机翼与水平方向的夹角为,
根据牛顿第二定律得:
解得机翼和水平面间夹角的正切值为:
答:机翼和水平面间夹角的正切值为。
【解析】滑翔机在水平面做匀速圆周运动,合力提供向心力,根据牛顿第二定律提供向心力即可求出机翼和水平面间夹角的正切值。
解决本题的关键理清滑翔机的运动情况,即水平面做圆周运动,根据牛顿第二定律求解。
15.【答案】解:小球靠重力和支持力的合力提供向心力,小球做圆周运动的半径为,根据力图可知,解得,所以。
答:此时小球离碗底的高度h为。
【解析】小球在光滑碗内靠重力和支持力的合力提供向心力,根据向心力和重力的关系求出小球与半球形碗球心连线与竖直方向的夹角,根据几何关系求出平面离碗底的距离h。
解决本题的关键知道小球做圆周运动向心力的来源,运用牛顿第二定律和几何关系进行求解。
16.【答案】解:小木块在竖直方向上受到的摩擦力与重力是一对平衡力,所以有:
根据滑动摩擦力公式:
联立解得:?N
小木块随圆周运动的向心力由圆筒内壁对木块的支持力提供,
根据牛顿第二定律得:
代入数据解得圆筒转动的角速度为:?
答:圆筒转动的角速度为。
【解析】物体在竖直方向受到重力与摩擦力,二者是平衡力,由摩擦力的公式即可求出弹力,由弹力提供向心力的公式即可求出。
本题考查了匀速圆周运动问题,解决此题得关键是要明确物体在圆筒内壁做匀速圆周运动,向心力是由筒壁对物体的支持力提供的。
17.【答案】解:设物体M和水平面保持相对静止。
当具有最小值时,M有向圆心运动趋势,故水平面对M的静摩擦力方向和指向圆心方向相反,且等于最大静摩擦力2N。
根据牛顿第二定律隔离M有:
??
?????解得
当具有最大值时,M有离开圆心趋势,水平面对M摩擦力方向指向圆心,大小也为2N。
再隔离M有:
??
??????
解得
所以范围是:
答:角速度在范围m会处于静止状态。
【解析】当角速度最小时,由于细绳的拉力作用,M有向圆心运动趋势,静摩擦力方向和指向圆心方向相反,并且达到最大值,由最大静摩擦力与细绳拉力的合力提供M的向心力。当角速度最大时,M有离开圆心趋势,静摩擦力方向指向圆心方向,并且达到最大值,由最大静摩擦力与细绳拉力的合力提供M的向心力。根据牛顿第二定律求解角速度及其范围。
本题考查应用牛顿定律处理临界问题的能力。当物体将滑动时,静摩擦力达到最大值。
第8页,共12页
