鲁科版_必修2_第3节 向心力的实例分析课件23张PPT
文档属性
| 名称 | 鲁科版_必修2_第3节 向心力的实例分析课件23张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-30 12:05:40 | ||
图片预览








文档简介
竖直平面内圆周运动的临界问题
竖直面内圆周运动
-----圆周运动实例
学习目标
1.了解竖直面内圆周运动的两类基本模型.
2.掌握变速圆周运动的特殊点的相关分析.
知识回顾:
1.向心力公式.
2.向心力的来源.
3.汽车过拱形桥的运动特点.
游乐项目-------过山车
过山车是一项刺激的游乐项目,让乘坐者体验超重失重带来的乐趣,过山车通过竖直面最高点不落下对速度有要求吗?
水流星表演中,过竖直面圆周最高点时,碗中的水不会流出,你知道原因吗?
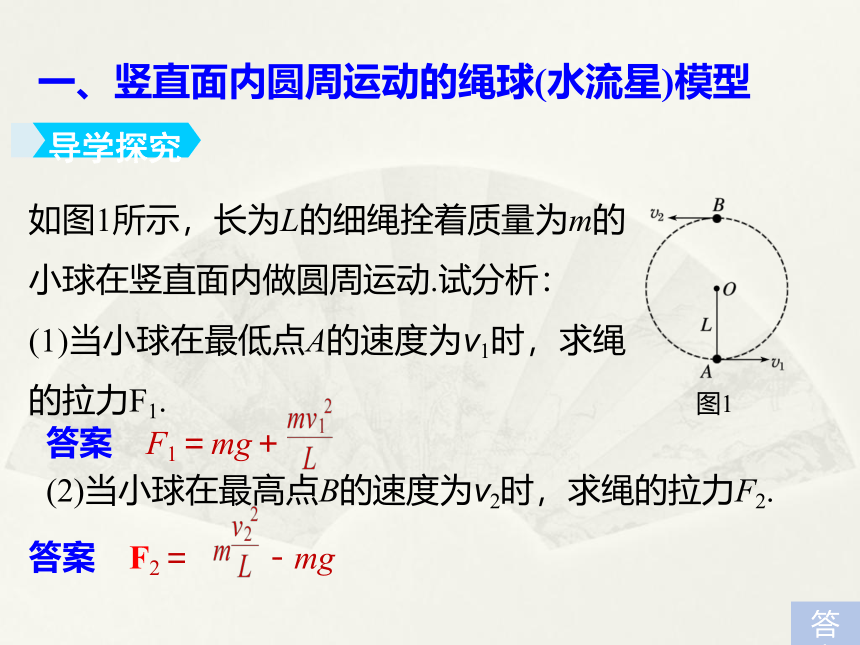
一、竖直面内圆周运动的绳球(水流星)模型
如图1所示,长为L的细绳拴着质量为m的小球在竖直面内做圆周运动.试分析:
(1)当小球在最低点A的速度为v1时,求绳的拉力F1.
答案
导学探究
图1
答案 F1=mg+
(2)当小球在最高点B的速度为v2时,求绳的拉力F2.
答案 F2= -mg
(3)小球过最高点的最小速度是多大?
答案
答案 由于绳不可能对球有向上的支持力,只能产生向下的拉力,由F2+mg= 可知,当F2=0时,v2最小,最小速度为v0=
(4)假设绳拉球过最高点时最小速度小于 ,则会产生什么样的后果?请总结绳拉球过最高点的条件.
答案
此时,重力mg的一部分提供向心力,剩余的另一部分力会使小球向下偏离圆周轨道,即小球此时不能过最高点做圆周运动,这之前已经脱离圆周轨道了.
绳拉球过最高点的条件是:v≥
(5)有一竖直放置、内壁光滑的圆环,其半径为r,质量为m的小球沿它的内表面做圆周运动,分析小球在最高点A的速度应满足什么条件?
答案
答案 与绳拉球模型相似,
在最高点A时,有FN+mg=
当FN=0时,v最小为v0= ,
当v=v0时,小球刚好能够通过最高点,
当v 当v>v0时,小球能够通过最高点.
FN
知识深化
绳球(光滑圆环内)模型通过最高点的条件 :V≥
请同学们填写导学案基础梳理
针对训练1.如图所示,用长为l的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是
A.小球在圆周最高点时所受的向心力一定为重力
B.小球在最高点时绳子的拉力不可能为零
C.若小球刚好能在竖直平面内做圆周运动,则其
在最高点的速率为
D.小球过最低点时绳子的拉力一定大于小球重力
答案
解析
√
√
二、竖直面内圆周运动的杆球(光滑管)模型
长为L的轻杆一端固定着一质量为m的小球,使小球在竖直面内做圆周运动.(如图5)
(1)当小球在最高点B的速度为v1 时,求杆对球的作用力.
答案
导学探究
图5
答案 设杆对它的作用力向下,则有mg+F=
当v1= 时,F=0.
当v1> 时,F>0,表示球受杆的作用力方向向下,表现为拉力.
当v1< 时,F<0,表示球受杆的作用力方向向上,表现为支持力.
对F取值进行分析
(2)杆拉球过最高点的最小速度为多少?
答案 由(1)中的分析可知,杆拉球过最高点的最小速度为零.
答案
提示 : 用笔扎上橡皮模仿杆球模型 ,并结合(1)中结果 分析
答案 设管壁对球的作用力向下,为FN.
答案
(3)试分析光滑圆管竖直轨道中,小球过最高点时受管壁的作用力与速度的关系?
当v= 时,FN=0,
当v> 时,FN>0,即外管壁对球有向下的压力;
当0 有向上的支持力.
FN
与杆球 模型受力情况类似
知识深化
杆球和管形轨道模型
1.最高点的最小速度
如图所示,细杆上固定的小球和管形轨道内运动的小球,由于杆和管在最高处能对小球产生向上的支持力,故小球恰能到达最高点的最小速度v=0,此时小球受到的支持力FN=mg.
2.小球通过最高点时,轨道对小球的弹力情况
(1)v> ,杆(管外侧)对球产生向下的拉力(压力),F随v 增大而增大.
(2)v= ,球在最高点只受重力,不受杆(管)的作用力,F=0.
(3)0 3.小球能过最高点的条件: V≥0
请同学们填写导学案基础梳理部分
图8
针对训练2.如图所示,半径为L的圆管轨道(圆管内径远小于轨道半径)竖直放置,管内壁光滑,管内有一个小球(小球直径略小于管内径)可沿管转动,设小球经过最高点P时的速度为v,则
A.v的最小值为
B.v若增大,球所需的向心力也增大
C.当v由 逐渐减小时,轨道对球的弹力也减小
D.当v由 逐渐增大时,轨道对球的弹力也增大
√
√
竖直面内圆周运动的分析方法:
1.明确运动的模型,是绳球模型还是杆球模型.
2.明确物体的临界状态,即在最高点时物体具有 最小速度时的受力特点.
3.分析物体在最高点及最低点的受力情况,根据牛顿第二定律列式求解.
3.一细绳与水桶相连,水桶中装有水,水桶与细绳一起在竖直平面内做圆周运动,如图3所示,水的质量m=0.5 kg,水的重心到转轴的距离l=50 cm.(g取10 m/s2)
(1)若在最高点水不流出来,求桶的最小速率;
(小数点后保留两位有效数字)
图3
(2)若在最高点水桶的速率v=3 m/s,求水对桶底的压力大小.
小试牛刀
解析 (1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,此时桶的速率最小.
则所求的最小速率为:v0= ≈2.24 m/s.
解析(2) 此时桶底对水有一向下的压力,设为FN,
则由牛顿第二定律有:FN+mg=
代入数据可得:FN=4 N.
由牛顿第三定律,水对桶底的压力:FN’=4 N.
4.长L=0.5 m的轻杆,其一端连接着一个零件A,A的质量m=2 kg.现让A在竖直平面内绕O点做匀速圆周运动,如图7所示.在A通过最高点时,求下列两种情况下A对杆的作用力大小(g=10 m/s2).
(1)A的速率为1 m/s;(2)A的速率为4 m/s.
答案
解析
小试牛刀
解析(1)以A为研究对象,设其受到杆的拉力为F,
则有mg+F=
代入数据v1=1 m/s,可得F=m( -g)=2×( -10) N=-16 N,即A受到杆的支持力为16 N.根据牛顿第三定律可得A对杆的作用力为压力,大小为16 N.
(2)代入数据v2=4 m/s,可得F′=m( -g)=2×( -10) N=44 N,即A受到杆的拉力为44 N.根据牛顿第三定律可得A对杆的作用力为拉力,大小为44 N.
竖直面内圆周运动
-----圆周运动实例
学习目标
1.了解竖直面内圆周运动的两类基本模型.
2.掌握变速圆周运动的特殊点的相关分析.
知识回顾:
1.向心力公式.
2.向心力的来源.
3.汽车过拱形桥的运动特点.
游乐项目-------过山车
过山车是一项刺激的游乐项目,让乘坐者体验超重失重带来的乐趣,过山车通过竖直面最高点不落下对速度有要求吗?
水流星表演中,过竖直面圆周最高点时,碗中的水不会流出,你知道原因吗?
一、竖直面内圆周运动的绳球(水流星)模型
如图1所示,长为L的细绳拴着质量为m的小球在竖直面内做圆周运动.试分析:
(1)当小球在最低点A的速度为v1时,求绳的拉力F1.
答案
导学探究
图1
答案 F1=mg+
(2)当小球在最高点B的速度为v2时,求绳的拉力F2.
答案 F2= -mg
(3)小球过最高点的最小速度是多大?
答案
答案 由于绳不可能对球有向上的支持力,只能产生向下的拉力,由F2+mg= 可知,当F2=0时,v2最小,最小速度为v0=
(4)假设绳拉球过最高点时最小速度小于 ,则会产生什么样的后果?请总结绳拉球过最高点的条件.
答案
此时,重力mg的一部分提供向心力,剩余的另一部分力会使小球向下偏离圆周轨道,即小球此时不能过最高点做圆周运动,这之前已经脱离圆周轨道了.
绳拉球过最高点的条件是:v≥
(5)有一竖直放置、内壁光滑的圆环,其半径为r,质量为m的小球沿它的内表面做圆周运动,分析小球在最高点A的速度应满足什么条件?
答案
答案 与绳拉球模型相似,
在最高点A时,有FN+mg=
当FN=0时,v最小为v0= ,
当v=v0时,小球刚好能够通过最高点,
当v
FN
知识深化
绳球(光滑圆环内)模型通过最高点的条件 :V≥
请同学们填写导学案基础梳理
针对训练1.如图所示,用长为l的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是
A.小球在圆周最高点时所受的向心力一定为重力
B.小球在最高点时绳子的拉力不可能为零
C.若小球刚好能在竖直平面内做圆周运动,则其
在最高点的速率为
D.小球过最低点时绳子的拉力一定大于小球重力
答案
解析
√
√
二、竖直面内圆周运动的杆球(光滑管)模型
长为L的轻杆一端固定着一质量为m的小球,使小球在竖直面内做圆周运动.(如图5)
(1)当小球在最高点B的速度为v1 时,求杆对球的作用力.
答案
导学探究
图5
答案 设杆对它的作用力向下,则有mg+F=
当v1= 时,F=0.
当v1> 时,F>0,表示球受杆的作用力方向向下,表现为拉力.
当v1< 时,F<0,表示球受杆的作用力方向向上,表现为支持力.
对F取值进行分析
(2)杆拉球过最高点的最小速度为多少?
答案 由(1)中的分析可知,杆拉球过最高点的最小速度为零.
答案
提示 : 用笔扎上橡皮模仿杆球模型 ,并结合(1)中结果 分析
答案 设管壁对球的作用力向下,为FN.
答案
(3)试分析光滑圆管竖直轨道中,小球过最高点时受管壁的作用力与速度的关系?
当v= 时,FN=0,
当v> 时,FN>0,即外管壁对球有向下的压力;
当0
FN
与杆球 模型受力情况类似
知识深化
杆球和管形轨道模型
1.最高点的最小速度
如图所示,细杆上固定的小球和管形轨道内运动的小球,由于杆和管在最高处能对小球产生向上的支持力,故小球恰能到达最高点的最小速度v=0,此时小球受到的支持力FN=mg.
2.小球通过最高点时,轨道对小球的弹力情况
(1)v> ,杆(管外侧)对球产生向下的拉力(压力),F随v 增大而增大.
(2)v= ,球在最高点只受重力,不受杆(管)的作用力,F=0.
(3)0
请同学们填写导学案基础梳理部分
图8
针对训练2.如图所示,半径为L的圆管轨道(圆管内径远小于轨道半径)竖直放置,管内壁光滑,管内有一个小球(小球直径略小于管内径)可沿管转动,设小球经过最高点P时的速度为v,则
A.v的最小值为
B.v若增大,球所需的向心力也增大
C.当v由 逐渐减小时,轨道对球的弹力也减小
D.当v由 逐渐增大时,轨道对球的弹力也增大
√
√
竖直面内圆周运动的分析方法:
1.明确运动的模型,是绳球模型还是杆球模型.
2.明确物体的临界状态,即在最高点时物体具有 最小速度时的受力特点.
3.分析物体在最高点及最低点的受力情况,根据牛顿第二定律列式求解.
3.一细绳与水桶相连,水桶中装有水,水桶与细绳一起在竖直平面内做圆周运动,如图3所示,水的质量m=0.5 kg,水的重心到转轴的距离l=50 cm.(g取10 m/s2)
(1)若在最高点水不流出来,求桶的最小速率;
(小数点后保留两位有效数字)
图3
(2)若在最高点水桶的速率v=3 m/s,求水对桶底的压力大小.
小试牛刀
解析 (1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,此时桶的速率最小.
则所求的最小速率为:v0= ≈2.24 m/s.
解析(2) 此时桶底对水有一向下的压力,设为FN,
则由牛顿第二定律有:FN+mg=
代入数据可得:FN=4 N.
由牛顿第三定律,水对桶底的压力:FN’=4 N.
4.长L=0.5 m的轻杆,其一端连接着一个零件A,A的质量m=2 kg.现让A在竖直平面内绕O点做匀速圆周运动,如图7所示.在A通过最高点时,求下列两种情况下A对杆的作用力大小(g=10 m/s2).
(1)A的速率为1 m/s;(2)A的速率为4 m/s.
答案
解析
小试牛刀
解析(1)以A为研究对象,设其受到杆的拉力为F,
则有mg+F=
代入数据v1=1 m/s,可得F=m( -g)=2×( -10) N=-16 N,即A受到杆的支持力为16 N.根据牛顿第三定律可得A对杆的作用力为压力,大小为16 N.
(2)代入数据v2=4 m/s,可得F′=m( -g)=2×( -10) N=44 N,即A受到杆的拉力为44 N.根据牛顿第三定律可得A对杆的作用力为拉力,大小为44 N.
同课章节目录
- 第1章 功和功率
- 导入 神奇的机械
- 第1节 机械功
- 第2节 功和能
- 第3节 功率
- 第4节 人与机械
- 第2章 能的转化与守恒
- 导入 从水车到核电站
- 第1节 动能的改变
- 第2节 势能的改变
- 第3节 能量守恒定律
- 第4节 能源与可持续发展
- 第3章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 竖直方向上的抛体运动
- 第3节 平抛运动
- 第4节 斜抛运动
- 第4章 匀速圆周运动
- 导入 身边的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 向心力与向心加速度
- 第3节 向心力的实例分析
- 第4节 离心运动
- 第5章 万有引力定律及其应用
- 导入 从嫦娥奔月到“阿波罗”上天
- 第1节 万有引力定律及引力常量的测定
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈追求
- 第6章 相对论与量子论初步
- 导入 迈入新世界
- 第1节 高速世界
- 第2节 量子世界
