鲁科版_必修2_第3节 向心力的实例分析课件25张PPT
文档属性
| 名称 | 鲁科版_必修2_第3节 向心力的实例分析课件25张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-30 00:00:00 | ||
图片预览








文档简介
专题 竖直面内的圆周运动与临界问题
第五章 曲线运动
杂技表演的“水流星”
“水流星”就是把总质量为M的盛有水的桶,系在长L的绳子一端,使桶在竖直平面内绕绳另一端做圆周运动,要使桶运动到最高点时水不会流出。表演过程中不管演员怎样抡,水都不会从杯里洒出,甚至杯子在竖直面内运动到最高点时,已经杯口朝下,水也不会从杯子里洒出,这是为什么?
问题1:绳拉球模型
长为r的细绳拴着质量为m 的小球在竖直平面内做圆周运动。
o
A
L
v1
B
v2
试分析:
(1)当小球在最低点A 的速度为v1时,绳的拉力与速度的关系如何?
(2)当小球在最高点B 的速度为v2 时,绳的拉力与速度的关系又如何?
v1
o
mg
F1
可见:小球速度V越大,绳的拉力越大
最低点:
得
o
思考:小球过最高点的最小速度是多少?
最高点:
v2
小球刚好能过最高点
F2
mg
(1)临界条件:当F2=0时,恰好由重力提供向心力
即
(临界速度)
速度V越大,绳的拉力越大
最小速度:
(2)当v< ,小球不能通过最高点
(3)当v≥ ,小球能够通过最高点
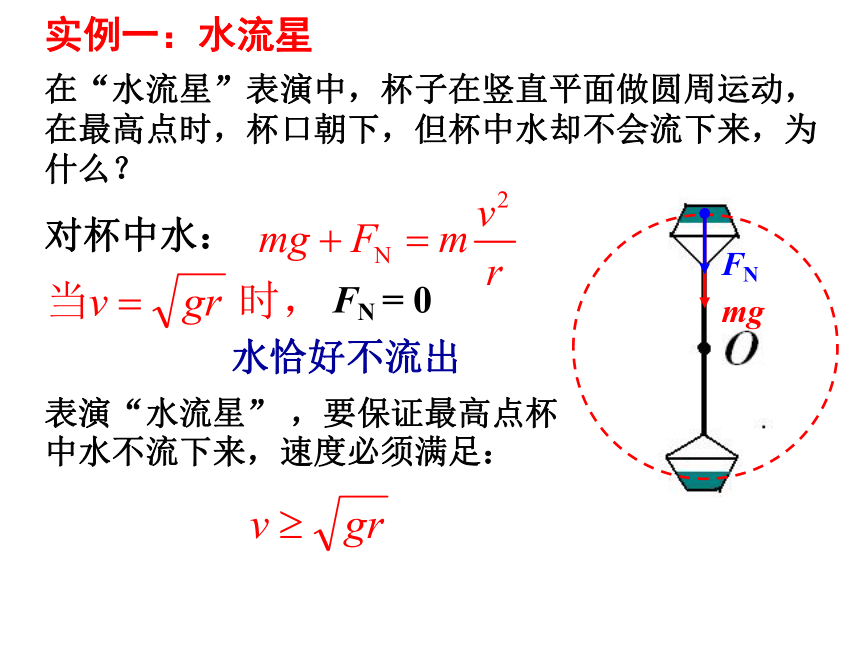
在“水流星”表演中,杯子在竖直平面做圆周运动,在最高点时,杯口朝下,但杯中水却不会流下来,为什么?
对杯中水:
mg
FN
FN = 0
水恰好不流出
表演“水流星” ,要保证最高点杯中水不流下来,速度必须满足:
实例一:水流星
(轻绳作用下物体的运动)杂技演员表演“水流星”,在长为1.6 m的细绳的一端,系一个与水的总质量为m=0.5 kg的盛水容器,以绳的另一端为圆心,在竖直平面内做圆周运动,如图1所示,若“水流星”通过最高点时的速率为4 m/s,则下列说法正确的是(g=10 m/s2)
A.“水流星”通过最高点时,有水从容器中流出
B.“水流星”通过最高点时,绳的张力及容器底
部受到的压力均为零
C.“水流星”通过最高点时,处于完全失重状态,
不受力的作用
D.“水流星”通过最高点时,绳子的拉力大小为5 N
√
图1
答案
思考:过山车为什么在最高点也不会掉下来?
实例二:过山车
问题2:小球沿竖直圆轨内侧运动
有一竖直放置、内壁光滑圆环,其半径为r,质量为m 的小球沿它的内表面做圆周运动,分析小球在最高点A 的速度应满足什么条件?
A
思考:小球过最高点的最小速度是多少?
小球刚好能够通过最高点
mg
FN
(1)临界条件:当FN=0时,
(临界速度)
最小速度:
(3)当v≥ ,小球能够通过最高点。
(2)当v< ,小球不能通过最高点
要保证过山车在最高点不掉下来,此时的速度必须满足:
FN
mg
(轨道约束下小球的运动)(多选)如图2所示,质量为m的小球在竖直平面内的光滑圆环内侧做圆周运动.圆环半径为R,小球经过圆环内侧最高点时刚好不脱离圆环,则其通过最高点时下列表述正确的是
A.小球对圆环的压力大小等于mg
B.重力mg充当小球做圆周运动所需的向心力
C.小球的线速度大小等于
D.小球的向心加速度大小等于g
图2
√
答案
√
√
问题3:杆球模型:
长为r的轻杆一端固定着一质量为m的小球,使小球在竖直平面内做圆周运动。
试分析:
(1)当小球在最低点A的速度为v2时,杆的受力与速度的关系怎样?
(2)当小球在最高点B的速度为v1时,杆的受力与速度的关系怎样?
A
B
v1
o
可见:球速度越大,杆的拉力越大
问题3:杆球模型:
A
B
最低点:
(拉力)
mg
F1
F3
mg
F2
v2
o
思考:在最高点时,⑴最小速度是多少?⑵临界速度是多少?⑶何时杆表现为拉力?⑷何时表现为支持力?⑸过最高点的条件是什么?
问题3:杆球模型:
A
B
最高点:
F3
mg
F2
v2
o
问题3:杆球模型:
A
B
最高点:
(1)最小速度:V=0, mg=F3(二力平衡)
(2)临界速度:F=0时, 恰好由重力提供向心力
(3)当0≤v< , 杆对球有向上的支持力
(4)当v> ,杆对球有向下的拉力
(5)过最高点的条件:v≥0
当V>V0时,速度越大,拉力越大
当V<V0时,速度越大,支持力越小,当V=V0时,拉力F=0
(轻杆作用下小球的运动)如图3所示,质量为m的小球固定在杆的一端,在竖直面内绕杆的另一端O做圆周运动.当小球运动到最高点时,瞬时速度为v= ,L是球心到O点的距离,则球对杆的作用力是
图3
答案
√
问题4:小球在竖直圆管内的运动
如图,有一内壁光滑、竖直放置的管型轨道,其半径为R,管内有一质量为m的小球有做圆周运动,小球的直径刚好略小于管的内径。问:
(1)小球运动到最高点时,速度与受力的关系如何?
(2)小球运动到最低点时,速度与受力的关系又是如何?
V2
mg
F1
V1
F2
F3
最高点:
;
最低点:
思考:小球在最高点的最小速度可以是多少?
最小速度v=0,此时mg=F3
mg
最高点:
;
V2
mg
F1
V1
F2
F3
mg
思考:
(2)什么时候内外管壁对小球都没有压力?(3)什么时候外管壁对小球有压力?
(4)什么时候内管壁对小球有支持力?
(1)在最高点时,小球的最小速度是多少?
(5)小球过最高点的条件是什么?
最高点:
(1)最小速度:V=0, mg=F3(二力平衡)
(2)临界速度:F=0时, 恰好由重力提供向心力
(3)当0≤v< , 内管壁对球有向上的支持力
(4)当v> ,外管壁对球有向下的压力
(5)过最高点的条件:v≥0
V2
mg
F1
V1
F2
F3
mg
图8
(球在管形轨道中的运动)(多选)如图所示,小球m在竖直放置的光滑的圆形管道内做圆周运动,下列说法正确的是
A.小球通过最高点时的最小速度是
B.小球通过最高点时的最小速度为零
C.小球在水平线ab以下的管道中运动时
外侧管壁对小球一定无作用力
D.小球在水平线ab以下的管道中运动时
外侧管壁对小球一定有作用力
答案
√
√
;
mg
O
外轨道
v1
o
mg
F1
o
F2
mg
mg
FN
mg
FN
mg
O
绳
如图所示,绳子系小球在竖直平面内运动和小球在光滑圆形轨道的内侧做圆周运动时小球的受力情况等效,故视为同一模型
细绳模型:
;
V2
mg
F1
V1
F2
F3
mg
F3
mg
F2
v2
o
B
v1
o
A
mg
F1
mg
O
N
轻杆
mg
O
N
圆管
如图所示,小球与轻杆相连或小球在光滑圆管内做圆周运动,其受力效果与轻杆模型相同
轻杆模型:
竖直平面内圆周运动的临界问题
物理情景
图示
在最高点的临界特点
做圆周运动条件
细绳拉着小球在竖直平面内运动
T=0
在最高点时速度应不小于
小球在竖直放置的光滑圆环内侧运动
N=0
在最高点时速度应不小于
小球固定在轻杆上在竖直面内运动
V>0
F向>0
F向=FT+mg 或F向=mg-Fn
在最高点速度应大于0
小球在竖直放置的光滑管中运动
V>0
F向>0
F向=FT+mg 或F向=mg-Fn
在最高点速度应大于0
mg
O
mg
O
N
临界问题:由于物体在竖直平面内做圆周运动的依托物(绳、轨道、轻杆、管道等)不同,所以物体恰好能通过最高点的临界条件也不同。
mg
O
N
绳
杆
mg
O
轨道
管道
物体在最高点的最小速度取决于该点所受的最小合外力。
第五章 曲线运动
杂技表演的“水流星”
“水流星”就是把总质量为M的盛有水的桶,系在长L的绳子一端,使桶在竖直平面内绕绳另一端做圆周运动,要使桶运动到最高点时水不会流出。表演过程中不管演员怎样抡,水都不会从杯里洒出,甚至杯子在竖直面内运动到最高点时,已经杯口朝下,水也不会从杯子里洒出,这是为什么?
问题1:绳拉球模型
长为r的细绳拴着质量为m 的小球在竖直平面内做圆周运动。
o
A
L
v1
B
v2
试分析:
(1)当小球在最低点A 的速度为v1时,绳的拉力与速度的关系如何?
(2)当小球在最高点B 的速度为v2 时,绳的拉力与速度的关系又如何?
v1
o
mg
F1
可见:小球速度V越大,绳的拉力越大
最低点:
得
o
思考:小球过最高点的最小速度是多少?
最高点:
v2
小球刚好能过最高点
F2
mg
(1)临界条件:当F2=0时,恰好由重力提供向心力
即
(临界速度)
速度V越大,绳的拉力越大
最小速度:
(2)当v< ,小球不能通过最高点
(3)当v≥ ,小球能够通过最高点
在“水流星”表演中,杯子在竖直平面做圆周运动,在最高点时,杯口朝下,但杯中水却不会流下来,为什么?
对杯中水:
mg
FN
FN = 0
水恰好不流出
表演“水流星” ,要保证最高点杯中水不流下来,速度必须满足:
实例一:水流星
(轻绳作用下物体的运动)杂技演员表演“水流星”,在长为1.6 m的细绳的一端,系一个与水的总质量为m=0.5 kg的盛水容器,以绳的另一端为圆心,在竖直平面内做圆周运动,如图1所示,若“水流星”通过最高点时的速率为4 m/s,则下列说法正确的是(g=10 m/s2)
A.“水流星”通过最高点时,有水从容器中流出
B.“水流星”通过最高点时,绳的张力及容器底
部受到的压力均为零
C.“水流星”通过最高点时,处于完全失重状态,
不受力的作用
D.“水流星”通过最高点时,绳子的拉力大小为5 N
√
图1
答案
思考:过山车为什么在最高点也不会掉下来?
实例二:过山车
问题2:小球沿竖直圆轨内侧运动
有一竖直放置、内壁光滑圆环,其半径为r,质量为m 的小球沿它的内表面做圆周运动,分析小球在最高点A 的速度应满足什么条件?
A
思考:小球过最高点的最小速度是多少?
小球刚好能够通过最高点
mg
FN
(1)临界条件:当FN=0时,
(临界速度)
最小速度:
(3)当v≥ ,小球能够通过最高点。
(2)当v< ,小球不能通过最高点
要保证过山车在最高点不掉下来,此时的速度必须满足:
FN
mg
(轨道约束下小球的运动)(多选)如图2所示,质量为m的小球在竖直平面内的光滑圆环内侧做圆周运动.圆环半径为R,小球经过圆环内侧最高点时刚好不脱离圆环,则其通过最高点时下列表述正确的是
A.小球对圆环的压力大小等于mg
B.重力mg充当小球做圆周运动所需的向心力
C.小球的线速度大小等于
D.小球的向心加速度大小等于g
图2
√
答案
√
√
问题3:杆球模型:
长为r的轻杆一端固定着一质量为m的小球,使小球在竖直平面内做圆周运动。
试分析:
(1)当小球在最低点A的速度为v2时,杆的受力与速度的关系怎样?
(2)当小球在最高点B的速度为v1时,杆的受力与速度的关系怎样?
A
B
v1
o
可见:球速度越大,杆的拉力越大
问题3:杆球模型:
A
B
最低点:
(拉力)
mg
F1
F3
mg
F2
v2
o
思考:在最高点时,⑴最小速度是多少?⑵临界速度是多少?⑶何时杆表现为拉力?⑷何时表现为支持力?⑸过最高点的条件是什么?
问题3:杆球模型:
A
B
最高点:
F3
mg
F2
v2
o
问题3:杆球模型:
A
B
最高点:
(1)最小速度:V=0, mg=F3(二力平衡)
(2)临界速度:F=0时, 恰好由重力提供向心力
(3)当0≤v< , 杆对球有向上的支持力
(4)当v> ,杆对球有向下的拉力
(5)过最高点的条件:v≥0
当V>V0时,速度越大,拉力越大
当V<V0时,速度越大,支持力越小,当V=V0时,拉力F=0
(轻杆作用下小球的运动)如图3所示,质量为m的小球固定在杆的一端,在竖直面内绕杆的另一端O做圆周运动.当小球运动到最高点时,瞬时速度为v= ,L是球心到O点的距离,则球对杆的作用力是
图3
答案
√
问题4:小球在竖直圆管内的运动
如图,有一内壁光滑、竖直放置的管型轨道,其半径为R,管内有一质量为m的小球有做圆周运动,小球的直径刚好略小于管的内径。问:
(1)小球运动到最高点时,速度与受力的关系如何?
(2)小球运动到最低点时,速度与受力的关系又是如何?
V2
mg
F1
V1
F2
F3
最高点:
;
最低点:
思考:小球在最高点的最小速度可以是多少?
最小速度v=0,此时mg=F3
mg
最高点:
;
V2
mg
F1
V1
F2
F3
mg
思考:
(2)什么时候内外管壁对小球都没有压力?(3)什么时候外管壁对小球有压力?
(4)什么时候内管壁对小球有支持力?
(1)在最高点时,小球的最小速度是多少?
(5)小球过最高点的条件是什么?
最高点:
(1)最小速度:V=0, mg=F3(二力平衡)
(2)临界速度:F=0时, 恰好由重力提供向心力
(3)当0≤v< , 内管壁对球有向上的支持力
(4)当v> ,外管壁对球有向下的压力
(5)过最高点的条件:v≥0
V2
mg
F1
V1
F2
F3
mg
图8
(球在管形轨道中的运动)(多选)如图所示,小球m在竖直放置的光滑的圆形管道内做圆周运动,下列说法正确的是
A.小球通过最高点时的最小速度是
B.小球通过最高点时的最小速度为零
C.小球在水平线ab以下的管道中运动时
外侧管壁对小球一定无作用力
D.小球在水平线ab以下的管道中运动时
外侧管壁对小球一定有作用力
答案
√
√
;
mg
O
外轨道
v1
o
mg
F1
o
F2
mg
mg
FN
mg
FN
mg
O
绳
如图所示,绳子系小球在竖直平面内运动和小球在光滑圆形轨道的内侧做圆周运动时小球的受力情况等效,故视为同一模型
细绳模型:
;
V2
mg
F1
V1
F2
F3
mg
F3
mg
F2
v2
o
B
v1
o
A
mg
F1
mg
O
N
轻杆
mg
O
N
圆管
如图所示,小球与轻杆相连或小球在光滑圆管内做圆周运动,其受力效果与轻杆模型相同
轻杆模型:
竖直平面内圆周运动的临界问题
物理情景
图示
在最高点的临界特点
做圆周运动条件
细绳拉着小球在竖直平面内运动
T=0
在最高点时速度应不小于
小球在竖直放置的光滑圆环内侧运动
N=0
在最高点时速度应不小于
小球固定在轻杆上在竖直面内运动
V>0
F向>0
F向=FT+mg 或F向=mg-Fn
在最高点速度应大于0
小球在竖直放置的光滑管中运动
V>0
F向>0
F向=FT+mg 或F向=mg-Fn
在最高点速度应大于0
mg
O
mg
O
N
临界问题:由于物体在竖直平面内做圆周运动的依托物(绳、轨道、轻杆、管道等)不同,所以物体恰好能通过最高点的临界条件也不同。
mg
O
N
绳
杆
mg
O
轨道
管道
物体在最高点的最小速度取决于该点所受的最小合外力。
同课章节目录
- 第1章 功和功率
- 导入 神奇的机械
- 第1节 机械功
- 第2节 功和能
- 第3节 功率
- 第4节 人与机械
- 第2章 能的转化与守恒
- 导入 从水车到核电站
- 第1节 动能的改变
- 第2节 势能的改变
- 第3节 能量守恒定律
- 第4节 能源与可持续发展
- 第3章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 竖直方向上的抛体运动
- 第3节 平抛运动
- 第4节 斜抛运动
- 第4章 匀速圆周运动
- 导入 身边的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 向心力与向心加速度
- 第3节 向心力的实例分析
- 第4节 离心运动
- 第5章 万有引力定律及其应用
- 导入 从嫦娥奔月到“阿波罗”上天
- 第1节 万有引力定律及引力常量的测定
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈追求
- 第6章 相对论与量子论初步
- 导入 迈入新世界
- 第1节 高速世界
- 第2节 量子世界
