人教版高中物理 选修3-4 第十五章 相对论简介 章末测试题 Word版含解析
文档属性
| 名称 | 人教版高中物理 选修3-4 第十五章 相对论简介 章末测试题 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 290.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-30 00:00:00 | ||
图片预览



文档简介
一、选择题(1~8题为单选,9~10题为多选,每小题4分,共40分)
1.对相对论的基本认识,下列说法正确的是( A )
A.相对论认为:真空中的光速在不同惯性参考系中都是相同的
B.爱因斯坦通过质能方程阐明了质量就是能量
C.在高速运动的飞船中的钟走得比地球上的钟快
D.我们发现竖直向上高速运动的球在水平方向上变扁了
解析:爱因斯坦的质能方程阐明了质量和能量的相互联系,质量和能量是物体存在的两种形式,质量和能量是不同的概念,B错误.再由相对论的基本原理可知,选项A正确,C、D错误.
2.如图所示,按照狭义相对论的观点,火箭B是“追赶”光的;火箭A是“迎着”光飞行的,若火箭相对地面的速度均为v,则两火箭上的观察者测出的光速分别为( B )
A.c+v,c-v
B.c,c
C.c-v,c+v
D.无法确定
解析:根据光速不变原理,观察者测出的光速都为c.
3.一高速列车通过洞口为圆形的隧道,列车上的司机对隧道的观察结果为( D )
A.洞口为椭圆形,长度变短
B.洞口为圆形,长度不变
C.洞口为椭圆形,长度不变
D.洞口为圆形,长度变短
解析:在运动方向上由于有“尺缩效应”,故隧道长度变短;在垂直运动方向上,没有“尺缩效应”,故洞口为圆形,故选D.
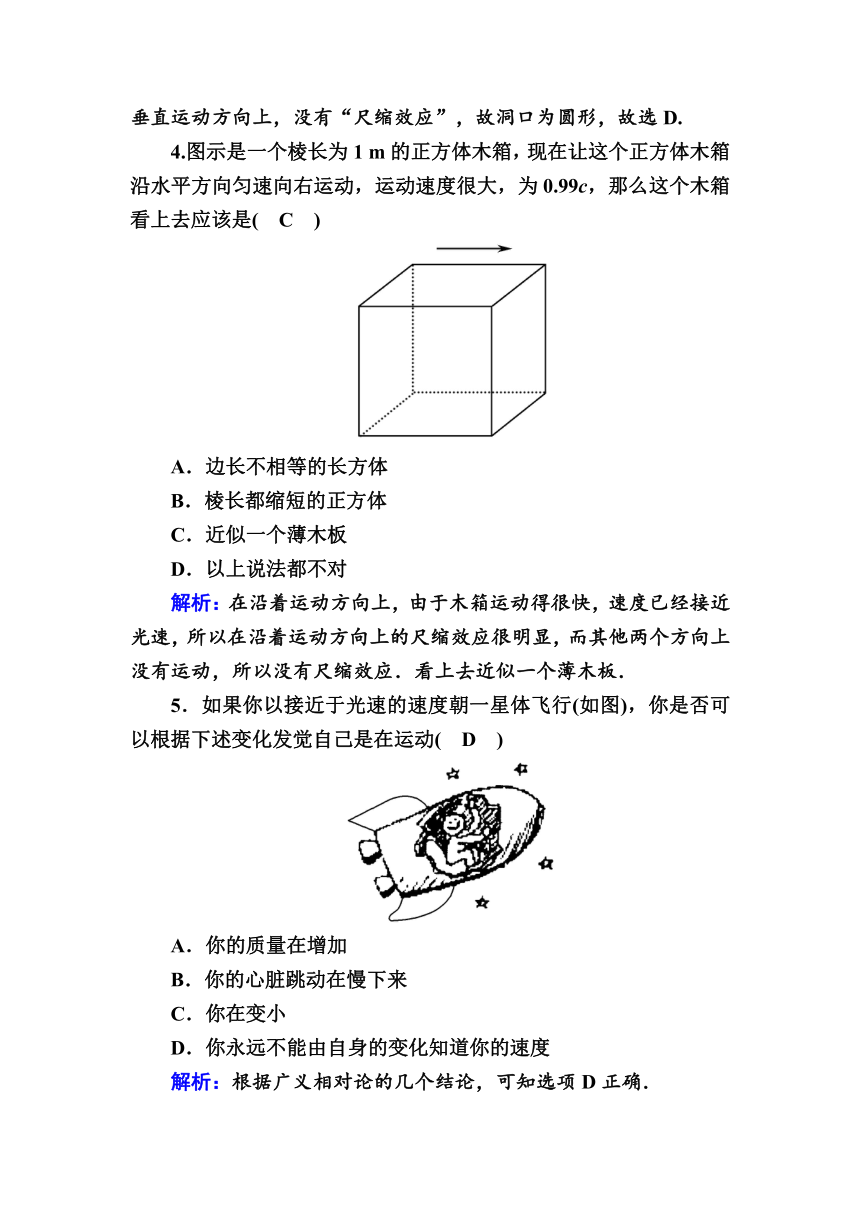
4.图示是一个棱长为1
m的正方体木箱,现在让这个正方体木箱沿水平方向匀速向右运动,运动速度很大,为0.99c,那么这个木箱看上去应该是( C )
A.边长不相等的长方体
B.棱长都缩短的正方体
C.近似一个薄木板
D.以上说法都不对
解析:在沿着运动方向上,由于木箱运动得很快,速度已经接近光速,所以在沿着运动方向上的尺缩效应很明显,而其他两个方向上没有运动,所以没有尺缩效应.看上去近似一个薄木板.
5.如果你以接近于光速的速度朝一星体飞行(如图),你是否可以根据下述变化发觉自己是在运动( D )
A.你的质量在增加
B.你的心脏跳动在慢下来
C.你在变小
D.你永远不能由自身的变化知道你的速度
解析:根据广义相对论的几个结论,可知选项D正确.
6.一艘宇宙飞船相对地球以0.8c的速度飞行,一光脉冲从船尾传到船头.飞船上的观察者测得飞船长为90
m,地球上的观察者测得光脉冲从船尾发出和到达船头两个事件的空间间隔为( C )
A.90
m
B.54
m
C.270
m
D.150
m
解析:由x=则有Δx=;
因为Δτ=,v=0.8c,
所以Δx=
m=270
m.
7.在某地发生两件事,静止位于该地的甲测得时间间隔为4
s,若相对甲做匀速直线运动的乙测得时间间隔为5
s,则乙相对于甲的运动速度是( B )
A.c
B.c
C.c
D.c
解析:将Δt=5
s,Δτ=4
s代入Δt=,
可解得v=c,正确选项为B.
8.如图,假设一根10
m长的梭镖以光速穿过一根10
m长的管子,它们的长度都是在静止状态下测量的.以下叙述中最好的描述了梭镖穿过管子的情况的是( D )
A.梭镖收缩变短,因此在某些位置上,管子能完全遮住它
B.管子收缩变短,因此在某些位置上,梭镖从管子的两端伸出来
C.两者都收缩,且收缩量相等,因此在某个位置,管子恰好遮住梭镖
D.所有这些都与观察者的运动情况有关
解析:如果你是在相对于管子静止的参考系中观察运动着的梭镖,那么梭镖看起来就比管子短,在某些位置梭镖会完全在管子内部,然而当你和梭镖一起运动时,你看到的管子就缩短了,所以在某些位置,你可以看到梭镖两端都伸出管子.
9.按照爱因斯坦的广义相对论,下列说法中正确的是( ABC )
A.天体之间的引力作用是时空弯曲的原因
B.光线经过太阳附近时会发生弯曲
C.氢原子发射的光从太阳传播到地球时,它的频率要比地球上氢原子发射的光的频率低
D.光在真空中任何情况下都是沿直线传播的
解析:根据广义相对论,物质的引力会使光线弯曲.引力越强弯曲越厉害,因此在地球上看到星体的位置与实际位置不符.在引力强的星球附近时间进程比较慢,原子发光的频率低,故A、B、C正确,D错误.
10.用著名的公式E=mc2(c是光速),可以计算核反应堆中为了产生一定的能量所需消耗的质量.下面的说法正确的是( AD )
A.同样的公式E=mc2也可以用来计算一个手电筒发出一定能量光时所丢失的质量
B.公式E=mc2适用于核反应堆中的核能,不适用于电池中的化学能
C.公式E=mc2只适用于计算核反应堆中为了产生一定的能量所需消耗的质量
D.公式E=mc2适用于任何类型的能量
解析:公式E=mc2适用于任何类型的能量,所以选项A、D正确.
二、填空题(共2小题,每小题6分,共12分)
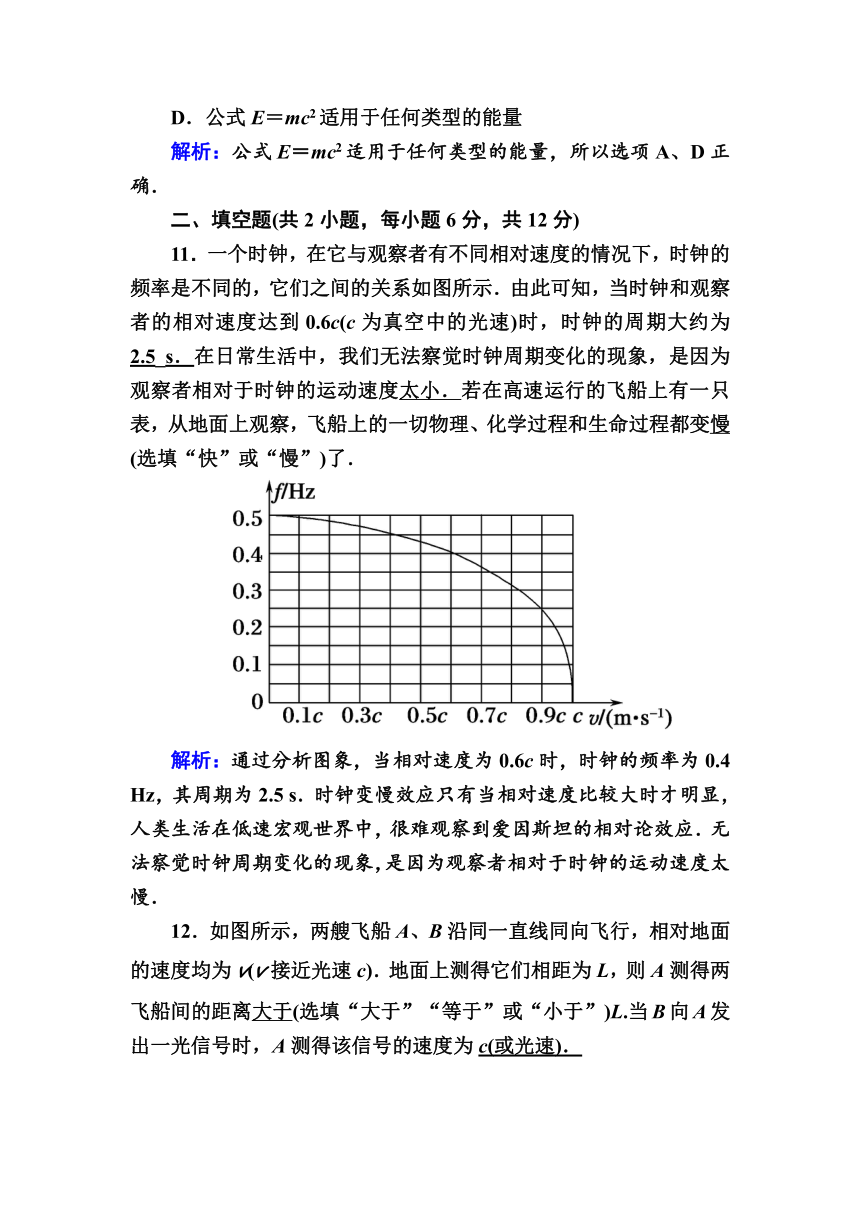
11.一个时钟,在它与观察者有不同相对速度的情况下,时钟的频率是不同的,它们之间的关系如图所示.由此可知,当时钟和观察者的相对速度达到0.6c(c为真空中的光速)时,时钟的周期大约为2.5_s.在日常生活中,我们无法察觉时钟周期变化的现象,是因为观察者相对于时钟的运动速度太小.若在高速运行的飞船上有一只表,从地面上观察,飞船上的一切物理、化学过程和生命过程都变慢(选填“快”或“慢”)了.
解析:通过分析图象,当相对速度为0.6c时,时钟的频率为0.4
Hz,其周期为2.5
s.时钟变慢效应只有当相对速度比较大时才明显,人类生活在低速宏观世界中,很难观察到爱因斯坦的相对论效应.无法察觉时钟周期变化的现象,是因为观察者相对于时钟的运动速度太慢.
12.如图所示,两艘飞船A、B沿同一直线同向飞行,相对地面的速度均为v(v接近光速c).地面上测得它们相距为L,则A测得两飞船间的距离大于(选填“大于”“等于”或“小于”)L.当B向A发出一光信号时,A测得该信号的速度为c(或光速).
解析:在飞船A上测量时飞船B是静止的,从地面上测量时两飞船都是运动的,由相对论的“尺缩效应”知运动长度要缩短,故从地面测得的飞船间距小.由光速不变原理知光信号的传播速度与参考系是无关的,故A测得该信号的速度仍为光速c.
三、计算题(共6小题,每小题8分,共48分)
13.一列速度接近光速的火车(静止时的长度比隧道的长度大)经过隧道时,站在地面上的人还看到两个闪电同时击中隧道的两端,但由于“动尺变短”效应,站在隧道旁边的人看到火车完全进入了隧道,刚好不会被闪电击中.但是,站在车上的人看到的却是隧道变得更短,不可能完全遮住整列火车,那么他看到的闪电会不会击中火车呢?并说明理由.
答案:不会 理由见解析
解析:站在隧道旁的人看到两个闪电是同时发生的,但站在火车里面的人看到的两个闪电却不是同时发生的,他看到的现象是:在火车前面的闪电先发生,经过一段时间后,火车后面的闪电才发生,而在这个时间间隔里面,列车已经前进了一段距离,所以车尾也不会被闪电击中.
14.列车以速度v匀速运动,车厢里的人量得车厢高为d,一相对于车厢静止的尺子的长度为L0.请思考:
(1)地面上的人量得的车厢高度为多少?
(2)地面上的人测得的尺子的长度为多少?
答案:(1)d (2)L0
解析:(1)由于在竖直方向上车厢没有运动,所以地面上的人量得车厢高度仍为d.
(2)由长度的相对性原理知,L=L0.
15.一电子以0.99c的速率运动.问:
(1)电子的总能量是多少?
(2)电子的经典力学的动能与相对论动能之比是多少?(电子静止质量m0=9.1×10-31
kg)
答案:(1)5.81×10-13
J (2)0.08
解析:(1)E=mc2=c2≈5.81×10-13
J.
(2)利用经典力学的公式计算
Ek′=m0v2=×9.1×10-31×(0.99c)2
J
≈4.01×10-14
J.
利用相对论计算
Ek=E-E0=(6.5-0.91)×10-30×9×1016
J
≈5.03×10-13
J,
所以,≈0.08.
16.地球上一观察者,看见一飞船A以速度2.5×108
m/s从他身边飞过,另一飞船B以速度2.0×108
m/s跟随A飞行.求:
(1)A上的乘客看到B的相对速度;
(2)B上的乘客看到A的相对速度.
答案:(1)-1.125×108
m/s
(2)1.125×108
m/s
解析:(1)A上的乘客看地面上的人以-2.5×108
m/s向后运动.
地面上的人看B以2.0×108
m/s向前运动,
则A上的乘客看到B的速度为
u==×108
m/s
≈-1.125×108
m/s.
(2)B上的乘客看到A的相对速度为1.125×108
m/s.
17.人马星座α星是离太阳系最近的恒星,它距地球4.3×1016
m.设有一宇宙飞船自地球往返于人马星座α星之间.若宇宙飞船的速度为0.999c,按地球上的时钟计算,飞船往返一次需多少时间?如以飞船上的时钟计算,往返一次的时间又为多少?
答案:9年 0.4年
解析:以地球上的时钟计算:
Δt==
s≈2.87×108
s≈9年;
若以飞船上的时钟计算:
因为Δt=,
所以得Δτ=Δt·
=2.87×108×
s
≈1.28×107
s≈0.4年.
18.设想地球上有一观察者测得一宇宙飞船以0.60c的速度向东飞行,5.0
s后该飞船将与一个以0.80c的速度向西飞行的彗星相碰撞.试问:
(1)飞船中的人测得彗星将以多大的速度向它运动?
(2)从飞船中的时钟来看,还有多少时间允许它离开航线,以避免与彗星碰撞?
答案:(1)0.946c (2)4.0
s
解析:(1)取地球为S系,飞船为S′系.向东为x轴正向.则S′系相对S系的速度v=0.60c,彗星相对S系的速度ux=-0.80c,由速度变换可得所求结果.
所以ux′=≈-0.946c,
即彗星以0.946c的速度向飞船靠近.
(2)把t0=t0′=0时的飞船状态视为一个事件,把飞船与彗星相碰视为第二个事件.这两个事件都发生在S′系中的同一地点(即飞船上),地球上的观察者测得这两个事件的时间间隔Δt=5.0
s,比固有时间要长,根据时间延缓效应可求出Δt′.即Δt==5
s,解得Δt′=4.0
s,即从飞船上的时钟来看,尚有4.0
s的时间允许它离开原来的航线.
1.对相对论的基本认识,下列说法正确的是( A )
A.相对论认为:真空中的光速在不同惯性参考系中都是相同的
B.爱因斯坦通过质能方程阐明了质量就是能量
C.在高速运动的飞船中的钟走得比地球上的钟快
D.我们发现竖直向上高速运动的球在水平方向上变扁了
解析:爱因斯坦的质能方程阐明了质量和能量的相互联系,质量和能量是物体存在的两种形式,质量和能量是不同的概念,B错误.再由相对论的基本原理可知,选项A正确,C、D错误.
2.如图所示,按照狭义相对论的观点,火箭B是“追赶”光的;火箭A是“迎着”光飞行的,若火箭相对地面的速度均为v,则两火箭上的观察者测出的光速分别为( B )
A.c+v,c-v
B.c,c
C.c-v,c+v
D.无法确定
解析:根据光速不变原理,观察者测出的光速都为c.
3.一高速列车通过洞口为圆形的隧道,列车上的司机对隧道的观察结果为( D )
A.洞口为椭圆形,长度变短
B.洞口为圆形,长度不变
C.洞口为椭圆形,长度不变
D.洞口为圆形,长度变短
解析:在运动方向上由于有“尺缩效应”,故隧道长度变短;在垂直运动方向上,没有“尺缩效应”,故洞口为圆形,故选D.
4.图示是一个棱长为1
m的正方体木箱,现在让这个正方体木箱沿水平方向匀速向右运动,运动速度很大,为0.99c,那么这个木箱看上去应该是( C )
A.边长不相等的长方体
B.棱长都缩短的正方体
C.近似一个薄木板
D.以上说法都不对
解析:在沿着运动方向上,由于木箱运动得很快,速度已经接近光速,所以在沿着运动方向上的尺缩效应很明显,而其他两个方向上没有运动,所以没有尺缩效应.看上去近似一个薄木板.
5.如果你以接近于光速的速度朝一星体飞行(如图),你是否可以根据下述变化发觉自己是在运动( D )
A.你的质量在增加
B.你的心脏跳动在慢下来
C.你在变小
D.你永远不能由自身的变化知道你的速度
解析:根据广义相对论的几个结论,可知选项D正确.
6.一艘宇宙飞船相对地球以0.8c的速度飞行,一光脉冲从船尾传到船头.飞船上的观察者测得飞船长为90
m,地球上的观察者测得光脉冲从船尾发出和到达船头两个事件的空间间隔为( C )
A.90
m
B.54
m
C.270
m
D.150
m
解析:由x=则有Δx=;
因为Δτ=,v=0.8c,
所以Δx=
m=270
m.
7.在某地发生两件事,静止位于该地的甲测得时间间隔为4
s,若相对甲做匀速直线运动的乙测得时间间隔为5
s,则乙相对于甲的运动速度是( B )
A.c
B.c
C.c
D.c
解析:将Δt=5
s,Δτ=4
s代入Δt=,
可解得v=c,正确选项为B.
8.如图,假设一根10
m长的梭镖以光速穿过一根10
m长的管子,它们的长度都是在静止状态下测量的.以下叙述中最好的描述了梭镖穿过管子的情况的是( D )
A.梭镖收缩变短,因此在某些位置上,管子能完全遮住它
B.管子收缩变短,因此在某些位置上,梭镖从管子的两端伸出来
C.两者都收缩,且收缩量相等,因此在某个位置,管子恰好遮住梭镖
D.所有这些都与观察者的运动情况有关
解析:如果你是在相对于管子静止的参考系中观察运动着的梭镖,那么梭镖看起来就比管子短,在某些位置梭镖会完全在管子内部,然而当你和梭镖一起运动时,你看到的管子就缩短了,所以在某些位置,你可以看到梭镖两端都伸出管子.
9.按照爱因斯坦的广义相对论,下列说法中正确的是( ABC )
A.天体之间的引力作用是时空弯曲的原因
B.光线经过太阳附近时会发生弯曲
C.氢原子发射的光从太阳传播到地球时,它的频率要比地球上氢原子发射的光的频率低
D.光在真空中任何情况下都是沿直线传播的
解析:根据广义相对论,物质的引力会使光线弯曲.引力越强弯曲越厉害,因此在地球上看到星体的位置与实际位置不符.在引力强的星球附近时间进程比较慢,原子发光的频率低,故A、B、C正确,D错误.
10.用著名的公式E=mc2(c是光速),可以计算核反应堆中为了产生一定的能量所需消耗的质量.下面的说法正确的是( AD )
A.同样的公式E=mc2也可以用来计算一个手电筒发出一定能量光时所丢失的质量
B.公式E=mc2适用于核反应堆中的核能,不适用于电池中的化学能
C.公式E=mc2只适用于计算核反应堆中为了产生一定的能量所需消耗的质量
D.公式E=mc2适用于任何类型的能量
解析:公式E=mc2适用于任何类型的能量,所以选项A、D正确.
二、填空题(共2小题,每小题6分,共12分)
11.一个时钟,在它与观察者有不同相对速度的情况下,时钟的频率是不同的,它们之间的关系如图所示.由此可知,当时钟和观察者的相对速度达到0.6c(c为真空中的光速)时,时钟的周期大约为2.5_s.在日常生活中,我们无法察觉时钟周期变化的现象,是因为观察者相对于时钟的运动速度太小.若在高速运行的飞船上有一只表,从地面上观察,飞船上的一切物理、化学过程和生命过程都变慢(选填“快”或“慢”)了.
解析:通过分析图象,当相对速度为0.6c时,时钟的频率为0.4
Hz,其周期为2.5
s.时钟变慢效应只有当相对速度比较大时才明显,人类生活在低速宏观世界中,很难观察到爱因斯坦的相对论效应.无法察觉时钟周期变化的现象,是因为观察者相对于时钟的运动速度太慢.
12.如图所示,两艘飞船A、B沿同一直线同向飞行,相对地面的速度均为v(v接近光速c).地面上测得它们相距为L,则A测得两飞船间的距离大于(选填“大于”“等于”或“小于”)L.当B向A发出一光信号时,A测得该信号的速度为c(或光速).
解析:在飞船A上测量时飞船B是静止的,从地面上测量时两飞船都是运动的,由相对论的“尺缩效应”知运动长度要缩短,故从地面测得的飞船间距小.由光速不变原理知光信号的传播速度与参考系是无关的,故A测得该信号的速度仍为光速c.
三、计算题(共6小题,每小题8分,共48分)
13.一列速度接近光速的火车(静止时的长度比隧道的长度大)经过隧道时,站在地面上的人还看到两个闪电同时击中隧道的两端,但由于“动尺变短”效应,站在隧道旁边的人看到火车完全进入了隧道,刚好不会被闪电击中.但是,站在车上的人看到的却是隧道变得更短,不可能完全遮住整列火车,那么他看到的闪电会不会击中火车呢?并说明理由.
答案:不会 理由见解析
解析:站在隧道旁的人看到两个闪电是同时发生的,但站在火车里面的人看到的两个闪电却不是同时发生的,他看到的现象是:在火车前面的闪电先发生,经过一段时间后,火车后面的闪电才发生,而在这个时间间隔里面,列车已经前进了一段距离,所以车尾也不会被闪电击中.
14.列车以速度v匀速运动,车厢里的人量得车厢高为d,一相对于车厢静止的尺子的长度为L0.请思考:
(1)地面上的人量得的车厢高度为多少?
(2)地面上的人测得的尺子的长度为多少?
答案:(1)d (2)L0
解析:(1)由于在竖直方向上车厢没有运动,所以地面上的人量得车厢高度仍为d.
(2)由长度的相对性原理知,L=L0.
15.一电子以0.99c的速率运动.问:
(1)电子的总能量是多少?
(2)电子的经典力学的动能与相对论动能之比是多少?(电子静止质量m0=9.1×10-31
kg)
答案:(1)5.81×10-13
J (2)0.08
解析:(1)E=mc2=c2≈5.81×10-13
J.
(2)利用经典力学的公式计算
Ek′=m0v2=×9.1×10-31×(0.99c)2
J
≈4.01×10-14
J.
利用相对论计算
Ek=E-E0=(6.5-0.91)×10-30×9×1016
J
≈5.03×10-13
J,
所以,≈0.08.
16.地球上一观察者,看见一飞船A以速度2.5×108
m/s从他身边飞过,另一飞船B以速度2.0×108
m/s跟随A飞行.求:
(1)A上的乘客看到B的相对速度;
(2)B上的乘客看到A的相对速度.
答案:(1)-1.125×108
m/s
(2)1.125×108
m/s
解析:(1)A上的乘客看地面上的人以-2.5×108
m/s向后运动.
地面上的人看B以2.0×108
m/s向前运动,
则A上的乘客看到B的速度为
u==×108
m/s
≈-1.125×108
m/s.
(2)B上的乘客看到A的相对速度为1.125×108
m/s.
17.人马星座α星是离太阳系最近的恒星,它距地球4.3×1016
m.设有一宇宙飞船自地球往返于人马星座α星之间.若宇宙飞船的速度为0.999c,按地球上的时钟计算,飞船往返一次需多少时间?如以飞船上的时钟计算,往返一次的时间又为多少?
答案:9年 0.4年
解析:以地球上的时钟计算:
Δt==
s≈2.87×108
s≈9年;
若以飞船上的时钟计算:
因为Δt=,
所以得Δτ=Δt·
=2.87×108×
s
≈1.28×107
s≈0.4年.
18.设想地球上有一观察者测得一宇宙飞船以0.60c的速度向东飞行,5.0
s后该飞船将与一个以0.80c的速度向西飞行的彗星相碰撞.试问:
(1)飞船中的人测得彗星将以多大的速度向它运动?
(2)从飞船中的时钟来看,还有多少时间允许它离开航线,以避免与彗星碰撞?
答案:(1)0.946c (2)4.0
s
解析:(1)取地球为S系,飞船为S′系.向东为x轴正向.则S′系相对S系的速度v=0.60c,彗星相对S系的速度ux=-0.80c,由速度变换可得所求结果.
所以ux′=≈-0.946c,
即彗星以0.946c的速度向飞船靠近.
(2)把t0=t0′=0时的飞船状态视为一个事件,把飞船与彗星相碰视为第二个事件.这两个事件都发生在S′系中的同一地点(即飞船上),地球上的观察者测得这两个事件的时间间隔Δt=5.0
s,比固有时间要长,根据时间延缓效应可求出Δt′.即Δt==5
s,解得Δt′=4.0
s,即从飞船上的时钟来看,尚有4.0
s的时间允许它离开原来的航线.
