21.2.4一元二次方程根与系数的关系 课件(共22张PPT)
文档属性
| 名称 | 21.2.4一元二次方程根与系数的关系 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 17:52:22 | ||
图片预览







文档简介
(共22张PPT)
一元二次方程根与系数的关系
数学人教版
九年级上
前两天悄悄地听到咱班的小明和小青的一段对话,内容如下:
小明:我说小青,我有一个秘密,你想听吗?
小青:什么秘密?
小明:你知道咱们可爱的张老师年龄到底有多大吗?
小青:哦?
新知导入
小明:呵呵,这绝对是个秘密,我不能直接告诉你,我这么
说吧:她的年龄啊是方程
的两根的积,回去你把两根求出来就知道了.
小青:咳,你难不住我,我不用求根就已经知道答案了,
而且我还告诉你,张老师的年龄啊还是方程
的两根的和呢.
小明:哈哈,你太有才了.对了,咱们应该也让同学们猜一猜,不解方程,能不能求出张老师的年龄.
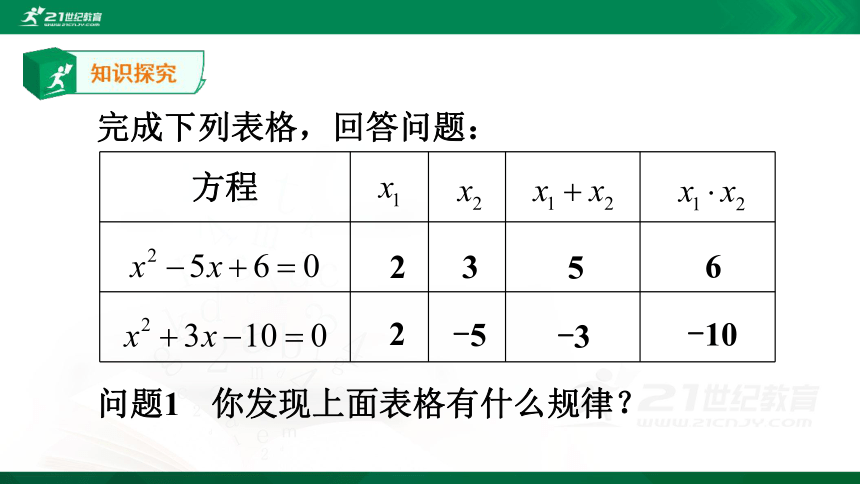
方程
完成下列表格,回答问题:
问题1
你发现上面表格有什么规律?
2
3
5
6
2
-10
-5
-3
用语言叙述:
两根之和为一次项系数的相反数;两根之积为常数项.
猜想:
当二次项系数为1时,设方程x2+px+q=0的两
根为x1,x2
,则
.
,
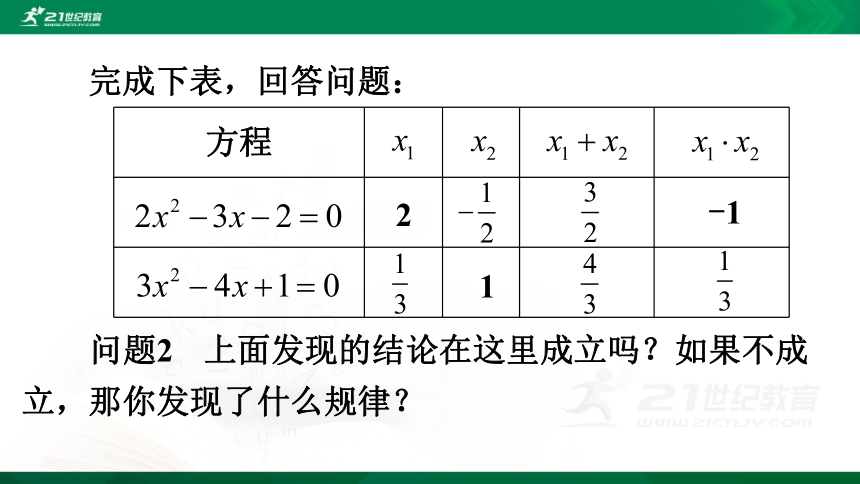
方程
完成下表,回答问题:
问题2
上面发现的结论在这里成立吗?如果不成立,那你发现了什么规律?
2
-1
1
一元二次方程的根与系数的关系
如果方程ax2+bx+c=0(a≠0)的两个根是x1
,x2,
那么x1+x2=
,x1x2=
.
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0.
用语言叙述:
两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数言项与二次项系数的比.
一元二次方程根与系数关系的证明:
因为一元二次方程
的两根是:
,
.
问题3
你能利用求根公式推导根与系数的关系吗?
x1x2=
由此可得
x1+x2=
+
=
=
,
=
=
=
.
例1
根据一元二次方程的根与系数的关系,
求下列方程两个根
的和与积:
(1)
(2)
;
(3)
;
.
(3)方程化为
.
.
解:(1)
,
.
(1)
(2)
;
(3)
;
.
(2)
,
在使用一元二次方程根与系数的关系时,应注意:
(1)不是一元二次方程一般形式的要先化成一般形式;
(2)在使用
时,
注意“-
”号不要漏写.
例2
已知方程
的一个根是-3,求另一个根及k的值.
解得k=3.
解:
设已知方程的另一个根是x1,由题意可得
.
故方程的另一个根为
.
所以
.
所以
.
1.求下列方程两个根
的和与积:
(1)
(2)
(3)
(4)
;
.
;
;
.
解:方程化为
.
(1)
;
(2)
;
.
解:
.
.
(4)
.
(3)
;
方程化为
解:
.
.
方程化为
解:
①×2-③,得-m=-8.∴m=8.
2.已知关于x的方程
的两个根是m和n,
且3m+2n=20,求k的值.
解:∵m,n是方程的两个根,
∴
将m=8代入①,得n=-2.
将m=8,n=-2代入②
,得k=8×(-2)=-16.
∵当k=-16时,
=36-4k=100>0,
∴k=-16.
1.一元二次方程的根与系数的关系
如果方程ax2+bx+c=0
(a≠0)
的两个根是x1,x2
,
2.用语言叙述
两根的和等于一次项系数与二次项系数的比的
相反数,两根的积等于常数项与二次项系数的比.
那么x1+x2=
,x1x2=
.
2.
已知
是一元二次方程
的两个
实数根,求
的值.
1.不解方程,求下列方程两个根x1,x2的和与积:
(2)
(1)
(4)
(3)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
一元二次方程根与系数的关系
数学人教版
九年级上
前两天悄悄地听到咱班的小明和小青的一段对话,内容如下:
小明:我说小青,我有一个秘密,你想听吗?
小青:什么秘密?
小明:你知道咱们可爱的张老师年龄到底有多大吗?
小青:哦?
新知导入
小明:呵呵,这绝对是个秘密,我不能直接告诉你,我这么
说吧:她的年龄啊是方程
的两根的积,回去你把两根求出来就知道了.
小青:咳,你难不住我,我不用求根就已经知道答案了,
而且我还告诉你,张老师的年龄啊还是方程
的两根的和呢.
小明:哈哈,你太有才了.对了,咱们应该也让同学们猜一猜,不解方程,能不能求出张老师的年龄.
方程
完成下列表格,回答问题:
问题1
你发现上面表格有什么规律?
2
3
5
6
2
-10
-5
-3
用语言叙述:
两根之和为一次项系数的相反数;两根之积为常数项.
猜想:
当二次项系数为1时,设方程x2+px+q=0的两
根为x1,x2
,则
.
,
方程
完成下表,回答问题:
问题2
上面发现的结论在这里成立吗?如果不成立,那你发现了什么规律?
2
-1
1
一元二次方程的根与系数的关系
如果方程ax2+bx+c=0(a≠0)的两个根是x1
,x2,
那么x1+x2=
,x1x2=
.
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0.
用语言叙述:
两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数言项与二次项系数的比.
一元二次方程根与系数关系的证明:
因为一元二次方程
的两根是:
,
.
问题3
你能利用求根公式推导根与系数的关系吗?
x1x2=
由此可得
x1+x2=
+
=
=
,
=
=
=
.
例1
根据一元二次方程的根与系数的关系,
求下列方程两个根
的和与积:
(1)
(2)
;
(3)
;
.
(3)方程化为
.
.
解:(1)
,
.
(1)
(2)
;
(3)
;
.
(2)
,
在使用一元二次方程根与系数的关系时,应注意:
(1)不是一元二次方程一般形式的要先化成一般形式;
(2)在使用
时,
注意“-
”号不要漏写.
例2
已知方程
的一个根是-3,求另一个根及k的值.
解得k=3.
解:
设已知方程的另一个根是x1,由题意可得
.
故方程的另一个根为
.
所以
.
所以
.
1.求下列方程两个根
的和与积:
(1)
(2)
(3)
(4)
;
.
;
;
.
解:方程化为
.
(1)
;
(2)
;
.
解:
.
.
(4)
.
(3)
;
方程化为
解:
.
.
方程化为
解:
①×2-③,得-m=-8.∴m=8.
2.已知关于x的方程
的两个根是m和n,
且3m+2n=20,求k的值.
解:∵m,n是方程的两个根,
∴
将m=8代入①,得n=-2.
将m=8,n=-2代入②
,得k=8×(-2)=-16.
∵当k=-16时,
=36-4k=100>0,
∴k=-16.
1.一元二次方程的根与系数的关系
如果方程ax2+bx+c=0
(a≠0)
的两个根是x1,x2
,
2.用语言叙述
两根的和等于一次项系数与二次项系数的比的
相反数,两根的积等于常数项与二次项系数的比.
那么x1+x2=
,x1x2=
.
2.
已知
是一元二次方程
的两个
实数根,求
的值.
1.不解方程,求下列方程两个根x1,x2的和与积:
(2)
(1)
(4)
(3)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
