人教版高中物理选修3-4课时作业 13-2 全反射 Word版含解析
文档属性
| 名称 | 人教版高中物理选修3-4课时作业 13-2 全反射 Word版含解析 |  | |
| 格式 | DOC | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-30 16:43:52 | ||
图片预览



文档简介
一、单选题(每小题6分,共30分)
1.关于全反射及其应用的认识,下列说法正确的是( D )
A.发生全反射时,仍有折射光线,只是折射光线非常弱,因此可以认为不存在折射光线而只有反射光线
B.全反射是反射光线与折射光线重合的一种现象
C.光线从光密介质射向光疏介质时,一定会发生全反射
D.光线从光疏介质射向光密介质时,不可能发生全反射
E.光纤通信是利用了光的折射原理
解析:发生全反射时,折射光线消失,A错,同理B错;由发生全反射的条件可知C错,D对;光纤通信是利用了光的全反射原理,E错.
2.一束光线穿过介质1、2、3时,光路如图所示,则( C )
A.介质1的折射率最大
B.介质2是光密介质
C.光在介质2中的速度最大
D.当入射角由45°逐渐增大时,在2、3分界面上可能发生全反射
解析:由图可知,光从介质1射入介质2中折射角大于入射角,则n1>n2.光从介质2射入介质3中折射角小于入射角,则n2<n3,据光的可逆性知,光从2射向1或从2射向3时,若入射角相等,从折射角上可判断n3>n1,所以有n3>n1>n2,即介质3折射率最大,故A错误.由对A的分析可知,相对来说,2是光疏介质,故B错误;根据公式:v=,因2的折射率最小,所以光在介质2中的传播速度最大,故C正确;当入射角由45°逐渐增大时,光从2到3是从光疏介质到光密介质,全反射只有光从光密介质射向光疏介质时才能发生,所以在此界面上不会发生全反射,故D错误.
3.如图所示,一个透明玻璃球的折射率为,一束足够强的细光束在过球心的平面内,以45°入射角由真空射入玻璃球后,在玻璃球与真空的交界面处发生多次反射和折射,从各个方向观察玻璃球,能看到从玻璃球内射出的光线的条数是( B )
A.2 B.3
C.4 D.5
解析:设第一个入射点为A,入射角i=45°,根据n=sini/sinr,n=,解得r=30°,光路图如图所示.所以,从各个方向观察玻璃球,能看到3条从玻璃球内射出的光线.
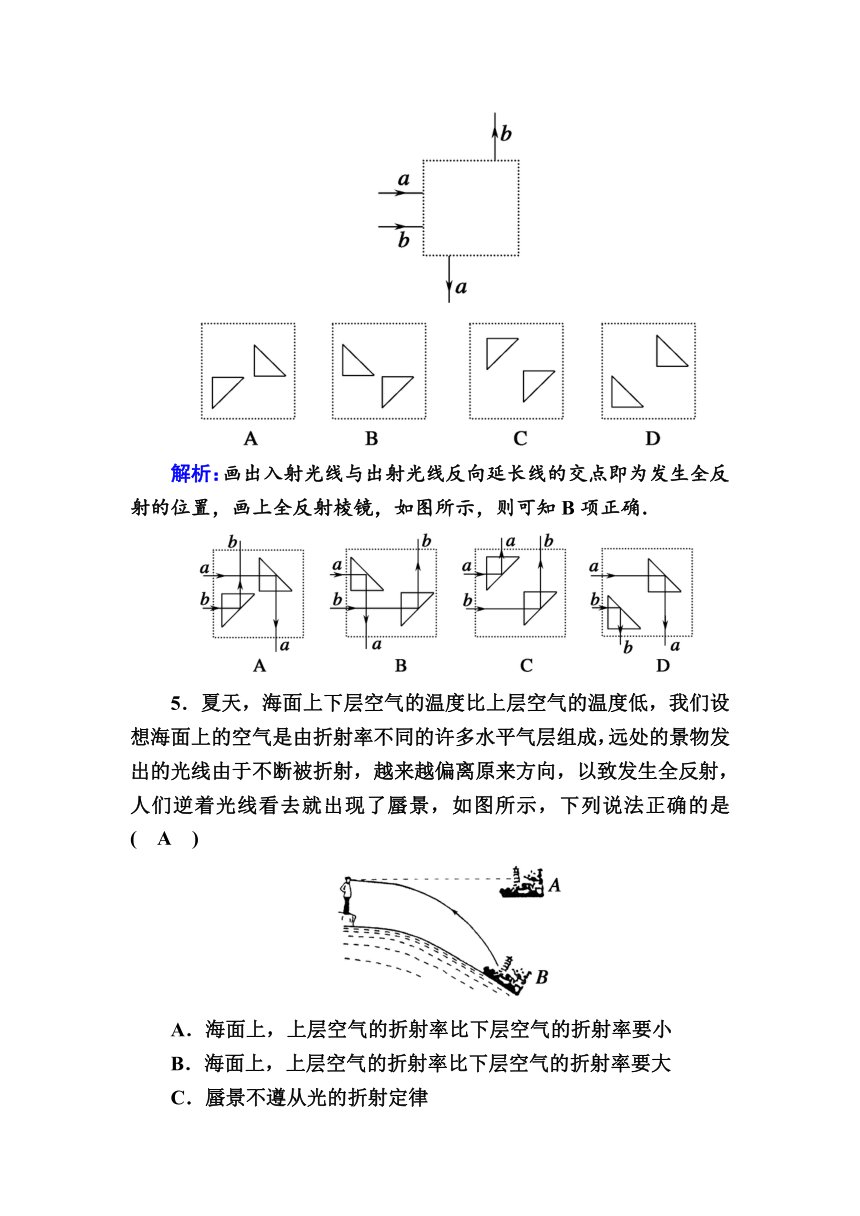
4.空气中两条光线a和b从方框左侧入射,分别从方框下方和上方射出,其框外光线如图所示.方框内有两个折射率n=1.5的玻璃全反射棱镜.选项图给出了两棱镜四种放置方式的示意图,其中能产生图示效果的是( B )
解析:画出入射光线与出射光线反向延长线的交点即为发生全反射的位置,画上全反射棱镜,如图所示,则可知B项正确.
5.夏天,海面上下层空气的温度比上层空气的温度低,我们设想海面上的空气是由折射率不同的许多水平气层组成,远处的景物发出的光线由于不断被折射,越来越偏离原来方向,以致发生全反射,人们逆着光线看去就出现了蜃景,如图所示,下列说法正确的是( A )
A.海面上,上层空气的折射率比下层空气的折射率要小
B.海面上,上层空气的折射率比下层空气的折射率要大
C.蜃景不遵从光的折射定律
D.B是蜃景,A是景物
解析:海面上,下层空气的温度比上层空气温度低,因此下层空气的折射率较大.入射光线从下层射向上层时,折射角比入射角大,这样在更上层的入射中入射角逐渐增大,据折射定律知最后会发生全反射现象.
二、多选题(每小题8分,共40分)
6.一束单色光从真空斜射向某种介质的表面,光路如图所示.下列说法中正确的是( AB )
A.光从真空射入介质后,频率不变
B.此介质的折射率等于
C.入射角大于45°时可能发生全反射现象
D.入射角小于30°时可能发生全反射现象
解析:光的频率由光源决定,在传播过程中频率不变,选项A正确;由折射定律n===,选项B正确;发生全反射的临界角C=arcsin=45°,只有当光线从光密介质射入光疏介质且入射角大于或等于临界角时才会发生全反射现象,所以选项C、D错误.
7.两束不同频率的平行单色光a、b分别由水射入空气发生如图所示的折射现象(α<β),下列说法正确的是( BC )
A.随着a、b入射角度的逐渐增加,a先发生全反射
B.水对a的折射率比水对b的折射率小
C.a、b在水中的传播速度va>vb
D.a、b入射角为0°时,没有光线射入空气中
解析:折射率n=,i为光在空气中传播路线与法线的夹角,α<β,故naCb,即b先发生全反射,A错.由n=(c为光在真空中的速度)可知,va>vb,C正确.入射角为0°时光线几乎全部进入空气中,故D错.
8.透明的水面上有一圆形荷叶,叶梗直立在水中,紧靠叶梗有一条小鱼,在岸上的人恰能看到小鱼,则( BC )
A.当小鱼潜深点时,人就看不见它了
B.当小鱼潜深点时,人照样能看见它
C.当小鱼上浮点时,人就看不见它了
D.当小鱼上浮点时,人照样能看见它
解析:小鱼潜深一点后,来自小鱼的光线的入射角变小,光线能折射出水面,人能看到鱼,同理,鱼上浮一点,入射角大于临界角,发生全反射,人就看不见它了,所以,B、C正确,A、D错误.
9.如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=r.现有一束单色光垂直于水平端面A射入透明柱体,只经过两次全反射就垂直于水平端面B射出.设透明柱体的折射率为n,光在透明柱体内传播的时间为t,若真空中的光速为c,则( AB )
A.n可能为 B.n可能为2
C.t可能为 D.t可能为
解析:
只经过两次全反射可知第一次入射角为45°,反射光路图如图所示.
根据全反射可知临界角C≤45°,再根据n=可知n≥;光在透明柱体中运动路程为L=4r,运动时间为t=L/v=4nr/c,则t≥4r/c,C、D均错.
10.如图所示为半圆形的玻璃砖,C为AB的中点.a、b两束不同频率的单色可见细光束垂直AB边从空气射入玻璃砖,且两束光在AB面上的入射点到C点的距离相等,两束光折射后相交于图中的P点,以下判断正确的是( BC )
A.在真空中,a光的传播速度大于b光的传播速度
B.若a、b两束光从同一介质射入真空中,a光发生全反射的临界角大于b光发生全反射的临界角
C.在真空中,a光的波长大于b光的波长
D.a光通过玻璃砖的时间大于b光通过玻璃砖的时间
解析:所有色光在真空中的传播速度相同,都为3×108 m/s,故A错误;由题图分析可知,玻璃砖对b光的折射率大于对a光的折射率,由sinC=分析得知,a光发生全反射的临界角大于b光发生全反射的临界角,故B正确.b光的折射率大,频率高,由c=λf得知,在真空中,a光的波长大于b光的波长,故C正确.由v=得知,a光在玻璃砖中的速度大,且a在玻璃砖中通过的路程短,所以a光通过玻璃砖的时间短,故D错误.
三、非选择题(共30分)
11.(14分)有人在河中游泳,头部露出水面,在某一位置当他低头向水中观察时,看到河底有一静止物体跟他眼睛正好在同一竖直线上,这个人再向前游12 m,正好不能看见此物体,求河深.(水的折射率为)
答案:10.6 m
解析:
如图所示,由题意知C为临界角,
则sinC== ①
从图可得sinC= ②
联立①②得:=,
解得h≈10.6 m.
12. (16分)如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(1)从球面射出的光线对应的入射光线与光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离.
答案:(1)R (2)2.74R
解析:
(1)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l.
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有nsinic=1②
由几何关系有sini=③
联立①②③式并利用题给条件,得l=R.④
(2)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有
nsini1=sinr1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有=⑥
由几何关系有∠C=r1-i1⑦
sini1=⑧
联立⑤⑥⑦⑧式及题给条件得
OC=R≈2.74R.⑨
1.关于全反射及其应用的认识,下列说法正确的是( D )
A.发生全反射时,仍有折射光线,只是折射光线非常弱,因此可以认为不存在折射光线而只有反射光线
B.全反射是反射光线与折射光线重合的一种现象
C.光线从光密介质射向光疏介质时,一定会发生全反射
D.光线从光疏介质射向光密介质时,不可能发生全反射
E.光纤通信是利用了光的折射原理
解析:发生全反射时,折射光线消失,A错,同理B错;由发生全反射的条件可知C错,D对;光纤通信是利用了光的全反射原理,E错.
2.一束光线穿过介质1、2、3时,光路如图所示,则( C )
A.介质1的折射率最大
B.介质2是光密介质
C.光在介质2中的速度最大
D.当入射角由45°逐渐增大时,在2、3分界面上可能发生全反射
解析:由图可知,光从介质1射入介质2中折射角大于入射角,则n1>n2.光从介质2射入介质3中折射角小于入射角,则n2<n3,据光的可逆性知,光从2射向1或从2射向3时,若入射角相等,从折射角上可判断n3>n1,所以有n3>n1>n2,即介质3折射率最大,故A错误.由对A的分析可知,相对来说,2是光疏介质,故B错误;根据公式:v=,因2的折射率最小,所以光在介质2中的传播速度最大,故C正确;当入射角由45°逐渐增大时,光从2到3是从光疏介质到光密介质,全反射只有光从光密介质射向光疏介质时才能发生,所以在此界面上不会发生全反射,故D错误.
3.如图所示,一个透明玻璃球的折射率为,一束足够强的细光束在过球心的平面内,以45°入射角由真空射入玻璃球后,在玻璃球与真空的交界面处发生多次反射和折射,从各个方向观察玻璃球,能看到从玻璃球内射出的光线的条数是( B )
A.2 B.3
C.4 D.5
解析:设第一个入射点为A,入射角i=45°,根据n=sini/sinr,n=,解得r=30°,光路图如图所示.所以,从各个方向观察玻璃球,能看到3条从玻璃球内射出的光线.
4.空气中两条光线a和b从方框左侧入射,分别从方框下方和上方射出,其框外光线如图所示.方框内有两个折射率n=1.5的玻璃全反射棱镜.选项图给出了两棱镜四种放置方式的示意图,其中能产生图示效果的是( B )
解析:画出入射光线与出射光线反向延长线的交点即为发生全反射的位置,画上全反射棱镜,如图所示,则可知B项正确.
5.夏天,海面上下层空气的温度比上层空气的温度低,我们设想海面上的空气是由折射率不同的许多水平气层组成,远处的景物发出的光线由于不断被折射,越来越偏离原来方向,以致发生全反射,人们逆着光线看去就出现了蜃景,如图所示,下列说法正确的是( A )
A.海面上,上层空气的折射率比下层空气的折射率要小
B.海面上,上层空气的折射率比下层空气的折射率要大
C.蜃景不遵从光的折射定律
D.B是蜃景,A是景物
解析:海面上,下层空气的温度比上层空气温度低,因此下层空气的折射率较大.入射光线从下层射向上层时,折射角比入射角大,这样在更上层的入射中入射角逐渐增大,据折射定律知最后会发生全反射现象.
二、多选题(每小题8分,共40分)
6.一束单色光从真空斜射向某种介质的表面,光路如图所示.下列说法中正确的是( AB )
A.光从真空射入介质后,频率不变
B.此介质的折射率等于
C.入射角大于45°时可能发生全反射现象
D.入射角小于30°时可能发生全反射现象
解析:光的频率由光源决定,在传播过程中频率不变,选项A正确;由折射定律n===,选项B正确;发生全反射的临界角C=arcsin=45°,只有当光线从光密介质射入光疏介质且入射角大于或等于临界角时才会发生全反射现象,所以选项C、D错误.
7.两束不同频率的平行单色光a、b分别由水射入空气发生如图所示的折射现象(α<β),下列说法正确的是( BC )
A.随着a、b入射角度的逐渐增加,a先发生全反射
B.水对a的折射率比水对b的折射率小
C.a、b在水中的传播速度va>vb
D.a、b入射角为0°时,没有光线射入空气中
解析:折射率n=,i为光在空气中传播路线与法线的夹角,α<β,故na
8.透明的水面上有一圆形荷叶,叶梗直立在水中,紧靠叶梗有一条小鱼,在岸上的人恰能看到小鱼,则( BC )
A.当小鱼潜深点时,人就看不见它了
B.当小鱼潜深点时,人照样能看见它
C.当小鱼上浮点时,人就看不见它了
D.当小鱼上浮点时,人照样能看见它
解析:小鱼潜深一点后,来自小鱼的光线的入射角变小,光线能折射出水面,人能看到鱼,同理,鱼上浮一点,入射角大于临界角,发生全反射,人就看不见它了,所以,B、C正确,A、D错误.
9.如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=r.现有一束单色光垂直于水平端面A射入透明柱体,只经过两次全反射就垂直于水平端面B射出.设透明柱体的折射率为n,光在透明柱体内传播的时间为t,若真空中的光速为c,则( AB )
A.n可能为 B.n可能为2
C.t可能为 D.t可能为
解析:
只经过两次全反射可知第一次入射角为45°,反射光路图如图所示.
根据全反射可知临界角C≤45°,再根据n=可知n≥;光在透明柱体中运动路程为L=4r,运动时间为t=L/v=4nr/c,则t≥4r/c,C、D均错.
10.如图所示为半圆形的玻璃砖,C为AB的中点.a、b两束不同频率的单色可见细光束垂直AB边从空气射入玻璃砖,且两束光在AB面上的入射点到C点的距离相等,两束光折射后相交于图中的P点,以下判断正确的是( BC )
A.在真空中,a光的传播速度大于b光的传播速度
B.若a、b两束光从同一介质射入真空中,a光发生全反射的临界角大于b光发生全反射的临界角
C.在真空中,a光的波长大于b光的波长
D.a光通过玻璃砖的时间大于b光通过玻璃砖的时间
解析:所有色光在真空中的传播速度相同,都为3×108 m/s,故A错误;由题图分析可知,玻璃砖对b光的折射率大于对a光的折射率,由sinC=分析得知,a光发生全反射的临界角大于b光发生全反射的临界角,故B正确.b光的折射率大,频率高,由c=λf得知,在真空中,a光的波长大于b光的波长,故C正确.由v=得知,a光在玻璃砖中的速度大,且a在玻璃砖中通过的路程短,所以a光通过玻璃砖的时间短,故D错误.
三、非选择题(共30分)
11.(14分)有人在河中游泳,头部露出水面,在某一位置当他低头向水中观察时,看到河底有一静止物体跟他眼睛正好在同一竖直线上,这个人再向前游12 m,正好不能看见此物体,求河深.(水的折射率为)
答案:10.6 m
解析:
如图所示,由题意知C为临界角,
则sinC== ①
从图可得sinC= ②
联立①②得:=,
解得h≈10.6 m.
12. (16分)如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(1)从球面射出的光线对应的入射光线与光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离.
答案:(1)R (2)2.74R
解析:
(1)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l.
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有nsinic=1②
由几何关系有sini=③
联立①②③式并利用题给条件,得l=R.④
(2)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有
nsini1=sinr1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有=⑥
由几何关系有∠C=r1-i1⑦
sini1=⑧
联立⑤⑥⑦⑧式及题给条件得
OC=R≈2.74R.⑨
