【A典学案】冲刺100分 七年级上专题复习第二讲 有理数及其运算课件(39张)
文档属性
| 名称 | 【A典学案】冲刺100分 七年级上专题复习第二讲 有理数及其运算课件(39张) |

|
|
| 格式 | rar | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 00:00:00 | ||
图片预览

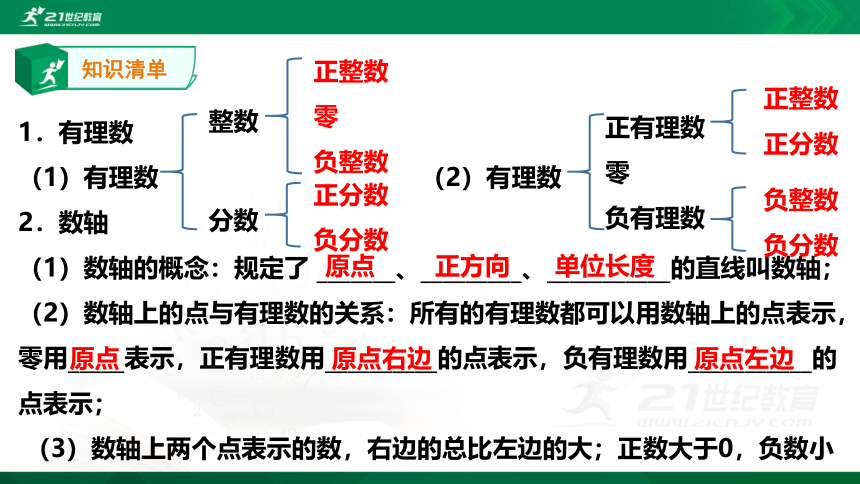










文档简介
第二讲 有理数及其运算
人教版 七年级上册
知识清单
1.有理数
(1)有理数 (2)有理数
2.数轴
(1)数轴的概念:规定了 _______、_________、___________的直线叫数轴;
(2)数轴上的点与有理数的关系:所有的有理数都可以用数轴上的点表示,零用_____表示,正有理数用__________的点表示,负有理数用___________的点表示;
(3)数轴上两个点表示的数,右边的总比左边的大;正数大于0,负数小
整数
分数
正整数
零
负整数
正分数
负分数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
原点 正方向 单位长度
原点
原点右边
原点左边
知识清单
于0,正数大于负数.
3.相反数
(1)概念:如果两个数只有_______不同,那么称其中一个数为另一个数的相反数,也称这个两个数互为相反数,特别地,0的相反数是___;
(2)几何意义:在数轴上,表示互为相反数的两个点,位于原点的_____,并且与原点的距离______ .
4.绝对值
(1)概念:在数轴上,一个数所对应的点与_______的距离叫做这个数的
符号
0
两侧
相等
原点
知识清单
绝对值;
(2)绝对值的求法:正数的绝对值是它_______,负数的绝对值是它的
__________,0的绝对值是 _____.
5.有理数的加法
(1)法则:同号两数相加,取______的符号,并把绝对值_______;异号两数相加,绝对值相等时和为_____,绝对值不相等时,取绝对值较____的数的符号,并用较大的绝对值减去较小的绝对值;一个数同_____相加,仍得这个数.
本身
相反数
0
相同
相加
0
大
0
知识清单
(2)运算律:①交换律:a+b=________;②结合律:(a+b)+c=
_______________.
6.有理数的减法
(1)法则:减去一个数,等于加上这个数的__________;
(2)字母表示:a-b=a+ _______ .
7.有理数的乘法
(1)法则:两数相乘,同号得 ___ ,异号得 ____ ,并把绝对值 相乘 ;任何数与0相乘,积仍为 ____ .
b+a
a+(b+c)
相反数
(-b)
正
负
0
知识清单
(2)推广:几个不为0的有理数相乘,积的符号由 _________ 的个数决定,当 ________ 为奇数个时,积为 ____ ;当 _______ 为偶数个时,积为 _____ .
(3)倒数:乘积为1的两个有理数互为倒数,如-2与_____;____与____.
(4)运算律:①交换律:a·b= ________ ;②结合律:(a·b)·c= ________ ;③乘法对加法的分配律:a(b+c)= ___________ .
8.有理数的除法
(1)法则一:两个有理数相除,同号得 _____ ,异号得 ____ ,并把绝
负因数
负因数
负
负因数
正
b·a
a·(b·c)
ab+ac
正
负
知识清单
对值 _______ ;0除以任何非0的数都得 _____ .
(2)法则二:除以一个数等于乘这个数的 ______ .
9.有理数的乘方
(1)意义:一般地,求n个相同因数a的 ____ 的运算叫做乘方;即=an,其中乘方的结果叫做 _____ ,a叫做 _______ ,n叫做 _______ ;
(2)乘方运算的符号法则:正数的任何次幂都是 _______ ,负数的奇数次幂是 ________ ,负数的偶数次幂是 ______ .
相除
0
倒数
积
幂
底数
指数
正数
负数
正数
知识清单
10.有理数的混合运算的运算顺序
先算 _______ ,再算 ______ ,最后算 _______ ;如果有括号,就先算 _________________ .
11.科学记数法
一般地,一个大于10的数可以表示成a×10n的形式,其中 ___ ≤a< ___ ,n是 __________ ,这种记数方法叫做科学记数法.
乘方
乘除
加减
括号里面的
1
10
正整数
典例精讲
类型之一 有理数的分类
【例1】把下列各数分别填在相应的括号内
正数:{ }; 负数:{ };
正整数:{ }; 正分数:{ };
负整数:{ }; 负分数:{ }.
典例精讲
[解析]正数: ;
负数: ;
正整数:{13,+6};
正分数: ;
负整数:{-2};
负分数:
变式训练
1.把下列各数分别填在相应的大括号内.
(1)整数集合:{ };
(2)分数集合:{ };
(3)负数集合:{ };
(4)自然数集合:{ }.
变式训练
【答案】(1)整数集合:{-5,10,0,2020,-69};
(2)分数集合: ;
(3)负数集合: ;
(4)自然数集合:{10,0,2020}.
典例精讲
类型之二 相反数和绝对值
【例2】绝对值等于3的数有____个,它们分别是_____,它们表示的是一对 ______数.
[解析]正数的绝对值是它本身,负数的绝对值是它的相反数,因此,绝对值等于一个正数的数有两个,它们互为相反数.
故答案为:2;3,-3;相反.
变式训练
2. 如果a的相反数是2,那么a等于( )
A.-2 B.2 C. D.
【答案】A
典例精讲
类型之三 数轴
【例3】有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.|a|>|b| B.ab>0
C.a+b>0 D.|a-b|>1
[解析]由数轴可得:-2<b<-1,0<a<1,则|a|<|b|,故选项A错误;
ab<0,故选项B错误;a+b<0,故选项C错误;|a-b|>1,正确.
故选D.
变式训练
3.有理数a,b在数轴上的位置如图所示,试化简|a-1|-|b-a|.
【答案】|a-1|-|b-a|=a-1+(b-a)=a-1+b-a=b-1.
典例精讲
类型之四 科学记数法
【例4】在我国南海某海域探明可燃冰储量约有194亿立方米,数字19400000000用科学记数法表示正确的是( )
A.1.94×10 B.0.194×10
C.19.4×10 D.1.94×10
典例精讲
[解析]用科学记数法表示一个大于10的数,就是把这个数表示为a×10 (其中a是整数位数只有一位的数,n是正整数)的形式.因此,准确地理解科学记数法的概念,紧紧抓住a,n的条件是解决此类题的关键.根据科学记数法表示数的规律,当原数大于10时,10的幂指数n=原数整数位数-1,
则19 400 000 000=1.9×10 .
故选A.
变式训练
4.某机构对30万人的调查显示,沉迷于手机上网的初中生大约占7%,则这部分沉迷于手机上网的初中生人数,可用科学记数法表示为( )
A.2.1×10 B.21×10
C.0.21×10 D.2.1×10
【答案】因为30万×7%=300 000×7%=21 000=2.1×10 .故选D.
典例精讲
类型之五 有理数的运算
【例5】计算:
典例精讲
[解析](1)原式=
(2)原式=
或原式=
变式训练
5.计算:
变式训练
【答案】(1)原式=
(2)原式=
(3)原式=
(4)原式=
典例精讲
类型之六 利用运算律简化运算
【例6】计算:
[解析] 原式=
变式训练
6.计算:
【答案】原式
典例精讲
类型之七 有理数运算的应用
【例7】某粮食加工厂刚加工了10箱袋装大米,每箱20袋,每袋800克.其中有一箱因为灌装机出现故障,每袋少了50克.厂长责令质检员只能称一次,就要查出是哪一箱出现问题.质检员小明思考了一下,他将10个箱子从1到10作了编号,然后从1号箱子中取出1袋大米,从2号箱子中取出2袋大米,依此类推.这样一共取了55袋大米,将它们一起称量,称得质量为43 800克,随后就找出了是哪一箱.你能明白其中的道理吗?
典例精讲
[解析]55袋大米的标准质量应为800×55=44 000(克),但是实际质量是43 800克,少了200克.
∵每袋中少了50克,200÷50=4,
∴是4号箱子中的大米不足.
变式训练
7.某出租车周日下午以钟楼为出发点,在东西方向的大街上行驶,规定向东为正,向西为负,行驶里程按照先后顺序记录如下(单位:km):
+9,-3,-5,+4,-8,+6,-3,-6,-4,+10.
(1)最后出租车离开钟楼多远?在钟楼的什么方向?
(2)若每千米的收费价格是2.4元,该出租车周日下午的营业额是多少?
变式训练
【答案】(1)+9-3-5+4-8+6-3-6-4+10=0,故该出租车正好在钟楼处.
(2)2.4×(|+9|+|-3|+|-5|+|+4|+|-8|+|+6|+|-3|+|-6|+|-4|+|+10|)
=2.4×58=139.2(元).
即该出租车周日下午的营业额是139.2元.
区校真题
1.(罗湖)在|-1|,(-1) ,(-1) ,-(-1)这四个数中,与-1互为相反数的数的个数有( )
A.1个 B.2个
C.3个 D.4个
2.(南山)根据国家气象局统计,全球平均每年发生雷电次数约为16 000 000次,将16 000 000用科学记数法表示为( )
A.1.6×10 B.1.6×10
C.16×10 D.1.6×10
C
B
区校真题
3.(宝安)已知有理数a,b在数轴上表示的点如图所示,则下列式子中不正确的是( )
A.a+b<0 B.b-a>0
C.ab>0 D.|a|-|b|>0
4.(坪山)下列运算正确的是( )
A.8-(-2)=8+2 B.
C.(-3)×(-4)=-7 D.2-7=(+2)+(+7)
C
A
区校真题
5.(百外)a,b,c三个数在数轴上的位置如图所示,则化简|a-b|-|a-c|的结果是_________________.
6.(罗湖)某品牌冰箱启动后开始降温,如果冰箱启动时的温度是10℃,每小时冰箱内部的温度降低5℃(降至设定温度后即停止降温),那么3小时后冰箱内部温度是 __________.
2a-b-c
-5℃
区校真题
7.(福田)计算:
(1)-8-(-9)+(-3);
【解答】(1)原式=-8+9-3=-2;
(2)原式=9-8-1=0;
(3)原式=1+3-2=2.
区校真题
8.(南山)我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将 化为分数形式
由于 =0.777…,设x=0.777…①
则10x=7.777…②
②-①得9x=7,解得x= ,于是得 = .
同理可得
区校真题
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
【基础训练】
(1) =_________, =__________;
(2) 将化为分数形式,写出推导过程;
【能力提升】
(3) =_______, =_____;(注:=0.315 315…,=2.018 18…)
【探索发现】
(4)①试比较 与1的大小: _______1(填“>”、“<”或“=”)
区校真题
②若已知 ,则 =___.(注: )
【解答】(1)由题意知 ,故答案为:
(2)
设x=0.232 323……①,则100x=23.232 3……②,
②-①,得:99x=23,解得: ,∴
(3)同理
故答案为:
区校真题
(4)①
故答案为:=.
②
故答案为: .
中考链接
1.下列各数中,负数是( )
A.-(-2) B.-|-2| C.(-2) D.(-2)
2.4月24日是中国航天日.1970年的这一天,我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射,标志着中国从此进入了太空时代,它的运行轨道,距地球最近点439 000米,将439 000用科学记数法表示应为( )
A.0.439×10 B.4.39×10
C.4.39×10 D.439×10
B
C
中考链接
3.如图,数轴上A,B两点所表示的数分别是-4和2,点C是线段AB的中点,则点C所表示的数是__________
-1
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
人教版 七年级上册
知识清单
1.有理数
(1)有理数 (2)有理数
2.数轴
(1)数轴的概念:规定了 _______、_________、___________的直线叫数轴;
(2)数轴上的点与有理数的关系:所有的有理数都可以用数轴上的点表示,零用_____表示,正有理数用__________的点表示,负有理数用___________的点表示;
(3)数轴上两个点表示的数,右边的总比左边的大;正数大于0,负数小
整数
分数
正整数
零
负整数
正分数
负分数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
原点 正方向 单位长度
原点
原点右边
原点左边
知识清单
于0,正数大于负数.
3.相反数
(1)概念:如果两个数只有_______不同,那么称其中一个数为另一个数的相反数,也称这个两个数互为相反数,特别地,0的相反数是___;
(2)几何意义:在数轴上,表示互为相反数的两个点,位于原点的_____,并且与原点的距离______ .
4.绝对值
(1)概念:在数轴上,一个数所对应的点与_______的距离叫做这个数的
符号
0
两侧
相等
原点
知识清单
绝对值;
(2)绝对值的求法:正数的绝对值是它_______,负数的绝对值是它的
__________,0的绝对值是 _____.
5.有理数的加法
(1)法则:同号两数相加,取______的符号,并把绝对值_______;异号两数相加,绝对值相等时和为_____,绝对值不相等时,取绝对值较____的数的符号,并用较大的绝对值减去较小的绝对值;一个数同_____相加,仍得这个数.
本身
相反数
0
相同
相加
0
大
0
知识清单
(2)运算律:①交换律:a+b=________;②结合律:(a+b)+c=
_______________.
6.有理数的减法
(1)法则:减去一个数,等于加上这个数的__________;
(2)字母表示:a-b=a+ _______ .
7.有理数的乘法
(1)法则:两数相乘,同号得 ___ ,异号得 ____ ,并把绝对值 相乘 ;任何数与0相乘,积仍为 ____ .
b+a
a+(b+c)
相反数
(-b)
正
负
0
知识清单
(2)推广:几个不为0的有理数相乘,积的符号由 _________ 的个数决定,当 ________ 为奇数个时,积为 ____ ;当 _______ 为偶数个时,积为 _____ .
(3)倒数:乘积为1的两个有理数互为倒数,如-2与_____;____与____.
(4)运算律:①交换律:a·b= ________ ;②结合律:(a·b)·c= ________ ;③乘法对加法的分配律:a(b+c)= ___________ .
8.有理数的除法
(1)法则一:两个有理数相除,同号得 _____ ,异号得 ____ ,并把绝
负因数
负因数
负
负因数
正
b·a
a·(b·c)
ab+ac
正
负
知识清单
对值 _______ ;0除以任何非0的数都得 _____ .
(2)法则二:除以一个数等于乘这个数的 ______ .
9.有理数的乘方
(1)意义:一般地,求n个相同因数a的 ____ 的运算叫做乘方;即=an,其中乘方的结果叫做 _____ ,a叫做 _______ ,n叫做 _______ ;
(2)乘方运算的符号法则:正数的任何次幂都是 _______ ,负数的奇数次幂是 ________ ,负数的偶数次幂是 ______ .
相除
0
倒数
积
幂
底数
指数
正数
负数
正数
知识清单
10.有理数的混合运算的运算顺序
先算 _______ ,再算 ______ ,最后算 _______ ;如果有括号,就先算 _________________ .
11.科学记数法
一般地,一个大于10的数可以表示成a×10n的形式,其中 ___ ≤a< ___ ,n是 __________ ,这种记数方法叫做科学记数法.
乘方
乘除
加减
括号里面的
1
10
正整数
典例精讲
类型之一 有理数的分类
【例1】把下列各数分别填在相应的括号内
正数:{ }; 负数:{ };
正整数:{ }; 正分数:{ };
负整数:{ }; 负分数:{ }.
典例精讲
[解析]正数: ;
负数: ;
正整数:{13,+6};
正分数: ;
负整数:{-2};
负分数:
变式训练
1.把下列各数分别填在相应的大括号内.
(1)整数集合:{ };
(2)分数集合:{ };
(3)负数集合:{ };
(4)自然数集合:{ }.
变式训练
【答案】(1)整数集合:{-5,10,0,2020,-69};
(2)分数集合: ;
(3)负数集合: ;
(4)自然数集合:{10,0,2020}.
典例精讲
类型之二 相反数和绝对值
【例2】绝对值等于3的数有____个,它们分别是_____,它们表示的是一对 ______数.
[解析]正数的绝对值是它本身,负数的绝对值是它的相反数,因此,绝对值等于一个正数的数有两个,它们互为相反数.
故答案为:2;3,-3;相反.
变式训练
2. 如果a的相反数是2,那么a等于( )
A.-2 B.2 C. D.
【答案】A
典例精讲
类型之三 数轴
【例3】有理数a,b在数轴上的位置如图所示,则下列选项正确的是( )
A.|a|>|b| B.ab>0
C.a+b>0 D.|a-b|>1
[解析]由数轴可得:-2<b<-1,0<a<1,则|a|<|b|,故选项A错误;
ab<0,故选项B错误;a+b<0,故选项C错误;|a-b|>1,正确.
故选D.
变式训练
3.有理数a,b在数轴上的位置如图所示,试化简|a-1|-|b-a|.
【答案】|a-1|-|b-a|=a-1+(b-a)=a-1+b-a=b-1.
典例精讲
类型之四 科学记数法
【例4】在我国南海某海域探明可燃冰储量约有194亿立方米,数字19400000000用科学记数法表示正确的是( )
A.1.94×10 B.0.194×10
C.19.4×10 D.1.94×10
典例精讲
[解析]用科学记数法表示一个大于10的数,就是把这个数表示为a×10 (其中a是整数位数只有一位的数,n是正整数)的形式.因此,准确地理解科学记数法的概念,紧紧抓住a,n的条件是解决此类题的关键.根据科学记数法表示数的规律,当原数大于10时,10的幂指数n=原数整数位数-1,
则19 400 000 000=1.9×10 .
故选A.
变式训练
4.某机构对30万人的调查显示,沉迷于手机上网的初中生大约占7%,则这部分沉迷于手机上网的初中生人数,可用科学记数法表示为( )
A.2.1×10 B.21×10
C.0.21×10 D.2.1×10
【答案】因为30万×7%=300 000×7%=21 000=2.1×10 .故选D.
典例精讲
类型之五 有理数的运算
【例5】计算:
典例精讲
[解析](1)原式=
(2)原式=
或原式=
变式训练
5.计算:
变式训练
【答案】(1)原式=
(2)原式=
(3)原式=
(4)原式=
典例精讲
类型之六 利用运算律简化运算
【例6】计算:
[解析] 原式=
变式训练
6.计算:
【答案】原式
典例精讲
类型之七 有理数运算的应用
【例7】某粮食加工厂刚加工了10箱袋装大米,每箱20袋,每袋800克.其中有一箱因为灌装机出现故障,每袋少了50克.厂长责令质检员只能称一次,就要查出是哪一箱出现问题.质检员小明思考了一下,他将10个箱子从1到10作了编号,然后从1号箱子中取出1袋大米,从2号箱子中取出2袋大米,依此类推.这样一共取了55袋大米,将它们一起称量,称得质量为43 800克,随后就找出了是哪一箱.你能明白其中的道理吗?
典例精讲
[解析]55袋大米的标准质量应为800×55=44 000(克),但是实际质量是43 800克,少了200克.
∵每袋中少了50克,200÷50=4,
∴是4号箱子中的大米不足.
变式训练
7.某出租车周日下午以钟楼为出发点,在东西方向的大街上行驶,规定向东为正,向西为负,行驶里程按照先后顺序记录如下(单位:km):
+9,-3,-5,+4,-8,+6,-3,-6,-4,+10.
(1)最后出租车离开钟楼多远?在钟楼的什么方向?
(2)若每千米的收费价格是2.4元,该出租车周日下午的营业额是多少?
变式训练
【答案】(1)+9-3-5+4-8+6-3-6-4+10=0,故该出租车正好在钟楼处.
(2)2.4×(|+9|+|-3|+|-5|+|+4|+|-8|+|+6|+|-3|+|-6|+|-4|+|+10|)
=2.4×58=139.2(元).
即该出租车周日下午的营业额是139.2元.
区校真题
1.(罗湖)在|-1|,(-1) ,(-1) ,-(-1)这四个数中,与-1互为相反数的数的个数有( )
A.1个 B.2个
C.3个 D.4个
2.(南山)根据国家气象局统计,全球平均每年发生雷电次数约为16 000 000次,将16 000 000用科学记数法表示为( )
A.1.6×10 B.1.6×10
C.16×10 D.1.6×10
C
B
区校真题
3.(宝安)已知有理数a,b在数轴上表示的点如图所示,则下列式子中不正确的是( )
A.a+b<0 B.b-a>0
C.ab>0 D.|a|-|b|>0
4.(坪山)下列运算正确的是( )
A.8-(-2)=8+2 B.
C.(-3)×(-4)=-7 D.2-7=(+2)+(+7)
C
A
区校真题
5.(百外)a,b,c三个数在数轴上的位置如图所示,则化简|a-b|-|a-c|的结果是_________________.
6.(罗湖)某品牌冰箱启动后开始降温,如果冰箱启动时的温度是10℃,每小时冰箱内部的温度降低5℃(降至设定温度后即停止降温),那么3小时后冰箱内部温度是 __________.
2a-b-c
-5℃
区校真题
7.(福田)计算:
(1)-8-(-9)+(-3);
【解答】(1)原式=-8+9-3=-2;
(2)原式=9-8-1=0;
(3)原式=1+3-2=2.
区校真题
8.(南山)我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将 化为分数形式
由于 =0.777…,设x=0.777…①
则10x=7.777…②
②-①得9x=7,解得x= ,于是得 = .
同理可得
区校真题
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
【基础训练】
(1) =_________, =__________;
(2) 将化为分数形式,写出推导过程;
【能力提升】
(3) =_______, =_____;(注:=0.315 315…,=2.018 18…)
【探索发现】
(4)①试比较 与1的大小: _______1(填“>”、“<”或“=”)
区校真题
②若已知 ,则 =___.(注: )
【解答】(1)由题意知 ,故答案为:
(2)
设x=0.232 323……①,则100x=23.232 3……②,
②-①,得:99x=23,解得: ,∴
(3)同理
故答案为:
区校真题
(4)①
故答案为:=.
②
故答案为: .
中考链接
1.下列各数中,负数是( )
A.-(-2) B.-|-2| C.(-2) D.(-2)
2.4月24日是中国航天日.1970年的这一天,我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射,标志着中国从此进入了太空时代,它的运行轨道,距地球最近点439 000米,将439 000用科学记数法表示应为( )
A.0.439×10 B.4.39×10
C.4.39×10 D.439×10
B
C
中考链接
3.如图,数轴上A,B两点所表示的数分别是-4和2,点C是线段AB的中点,则点C所表示的数是__________
-1
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
