华师大版数学八年级上册期中考试复习学案
文档属性
| 名称 | 华师大版数学八年级上册期中考试复习学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 126.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-03 00:00:00 | ||
图片预览




文档简介
课题:第12章 数的开方
学习目标:通过复习,系统掌握本章知识,能运用相关知识解决相关问题,形成技能。
重点:本章知识点。
难点:应用。
一、知识点归纳:
1、概念:
(1)平方根:如果一个数的 等于a,那么这个数叫做a的 。
(2) 叫做a的算术平方根。0的算术平方根是 。
(3)如果一个数的 等于a,那么这个数就叫做a的立方根(也叫做 次方根)
(4)无理数: 叫做无理数. 不能开尽根的根号式及∏都是 。
(5)无理数与有理数统称为 .
(6)开平方:求一个数的 的运算,叫做开平方。
(7)开立方:求一个数的 的运算,叫做开立方。
2、实数的分类:(识记)
3、实数与数轴上的点是 的。
4、法则:
(1)一个正数有两 个平方根,它们互为 ;0的平方根是 ;负数 平方根.
(2)任何数都有 根,正数的立方根是 数,负数的立方根是 数,0的立方根是
二、典型例题:
例1、把下列各数填入相应的大括号内
, -3, 0, 3.1415 , , , , , ,
, 1.121221222122221… (两个1之间依次多个2)
(1)无理数集合: …;
(2)非负数集合: …;
(3)整数集合: …;
(4)分数集合: …。
例2、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是
A. B. 1.4 C. D.
例3、实数p在数轴上的位置如图所示,
化简______________;
例4、已知数a满足,求a-20002的值。
解:
三、基础练习:(课堂内不能完成的作为课后作业)
1、填空题
(1)的算术平方根是______.
(2)(-)2002·(+)2003=______.
(3)如果=2,那么(x+3)2=______.
(4)若=,那么的值是______.
(5)若xy=-,x-y=5-1,则(x+1)(y-1)=______.
(6)实数a,b在数轴上所对应的点的位置如图所示,则2a___________0,
a+b__________0,-|b-a|________0,化简|2a|-|a+b|=________.
(7)的相反数是______,-的倒数是______.
(8),则x的取值范围是__________.
(9)若的平方根是±3,则a=__________.
(10)当x=__________时,有最小值为__________.
(11)若与|x+y-3|互为相反数,则x=__________,y=__________.
(12)y=+2,则x=__________,y=__________.
2、选择:
(1)的平方根是( )A.3 B.-3 C.± D.
(2)下列说法中正确的是( )
A.任何数都有平方根 B.一个正数的平方根的平方就是它的本身
C.只有正数才有算术平方根 D.不是正数没有平方根
(3) 如果+有意义,那么代数式|x-1|+的值为( )
A.±8 B.8 C.与x的值无关 D.无法确定
(4)下列各式无意义的是( )A.- B. C. D.
(5) 在实数0.3,0,,,0.123456…中,其中无理数的个数是( )
A.2 B.3 C.4 D.5
(6)(-23)2的平方根是( )A.±8 B.8 C.-8 D.不存在
(7)一个自然数的算术平方根是x,则下一个自然数的算术平方根是( )
A.x+1 B.x2+1 C. D.
(8)使有意义的x的值是( )
A.正数 B.负数 C.0 D.非正数
3、计算:
(1)-+. (2)
(3) (4)
4、已知实数满足,求的值.
5、已知实数在数轴上的对应点如图所示,化简
6、已知的小数部分为,求的值。
7、已知某数有两个平方根分别是a+3与2a-15,求这个数
8、已知5+的小数部分为a,5-的小数部分为b,求:a+b的值;
9、已知x,y满足+3,求yx的平方根和算术平方根。
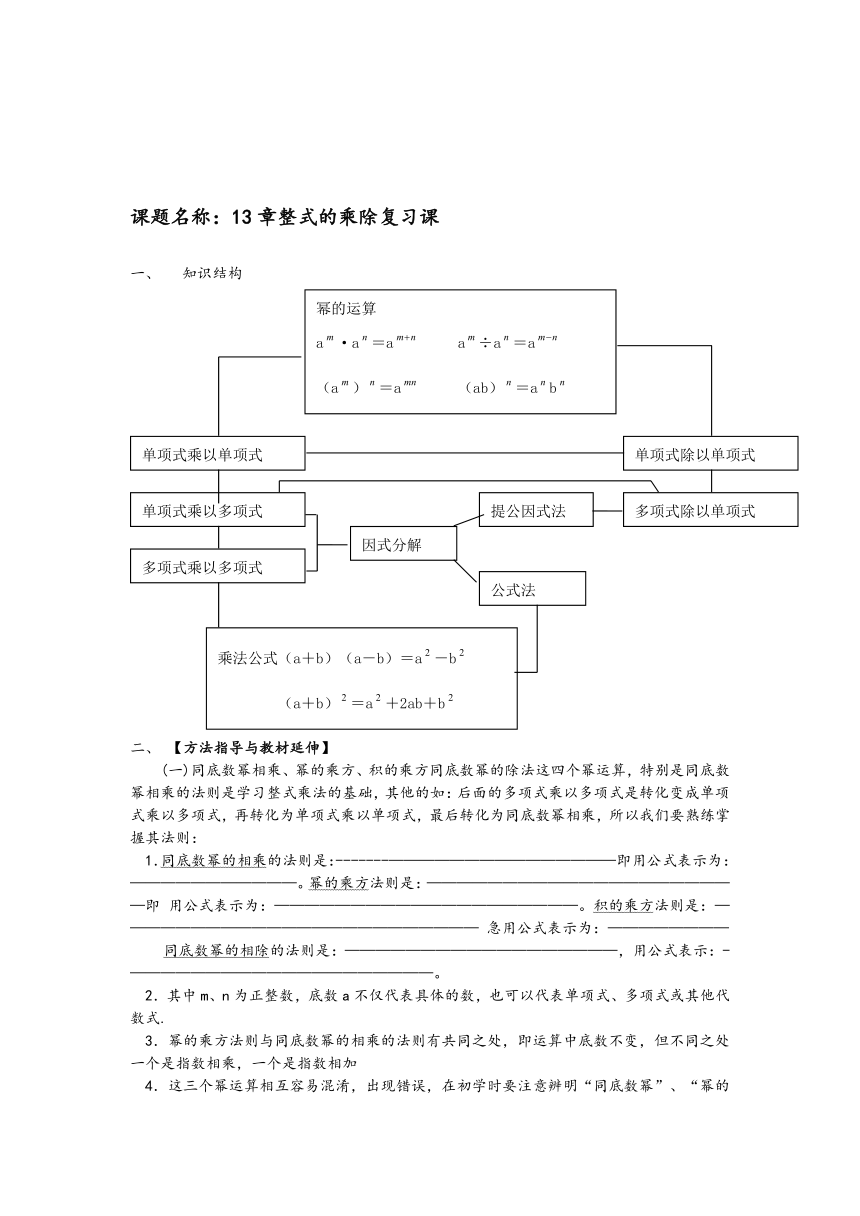
课题名称:13章整式的乘除复习课
知识结构
二、 【方法指导与教材延伸】
(一)同底数幂相乘、幂的乘方、积的乘方同底数幂的除法这四个幂运算,特别是同底数幂相乘的法则是学习整式乘法的基础,其他的如:后面的多项式乘以多项式是转化变成单项式乘以多项式,再转化为单项式乘以单项式,最后转化为同底数幂相乘,所以我们要熟练掌握其法则:
1.同底数幂的相乘的法则是:-------———————————————即用公式表示为:———————————。幂的乘方法则是:—————————————————————即 用公式表示为:————————————————————。积的乘方法则是:———————————————————————— 急用公式表示为:————————
同底数幂的相除的法则是:——————————————————,用公式表示:-————————————————————。
2.其中m、n为正整数,底数a不仅代表具体的数,也可以代表单项式、多项式或其他代数式.
3.幂的乘方法则与同底数幂的相乘的法则有共同之处,即运算中底数不变,但不同之处一个是指数相乘,一个是指数相加
4.这三个幂运算相互容易混淆,出现错误,在初学时要注意辨明“同底数幂”、“幂的乘方”、“积的乘方”等基本概念,对公式的记忆要联系相应的文字表述,运用法则计算时,要注意识别是同底数幂的相乘、幂的乘方还是积的乘方,法则中各字母分别代表什么?再对照法则运算.
(二)整式的乘法
1.单项式与单项式相乘:
由单项式与单项式法则可知,单项式与单项式相乘实为完成三项工作:(1)————————————————————————(2)——————————————(3)——————————————————————,单项式乘法法则对两个以上单项式相乘同样成立。
2.单项式与多项式相乘:
单项式与多项式相乘,实际上是转化为————————————————————,即———————————————————————————用公式表示为—————。
单项式与多项式相乘,结果是多项式,积的项数与因式中多项式的项数相同.
3.多项式与多项式相乘:
多项式与多项式相乘,实际上是先转化为单项式与多项式相乘,即将一个多项式看成一个整体,即(m+n)(a+b)=a(m+n)+b(m+n),再用一次单项式与多项式相乘,得(m+n)(a+b)=ma+n a+m b+b n.
多项式乘以多项式其积仍是多项式,积的次数等于两个多项式的次数之和,积的项数在末合并同类项之前等于两个多项式项数之和.
(三)乘法公式
1.“两数和乘以两数差:————————————————————,用公式表示为:————————————,应用这个乘法公式计算时,应掌握公式的特征:① 公式的左边是两个二项式相乘;并且这两个二项式中有一项是完全相同的项a,另一项是相反数项b;② 公式的右边是相同项的平方a2减去相反数项的平方b2.
公式中的a和b,可以是单项式,也可以是多项式或具体数字.
2.“两数和的平方:————————————————————”.即用公式表示:——————————————————————要理解公式的特征:① 公式的左边是一个二项式的平方,右边是一个二次三项式.公式的适用范围:公式中的a和b可以是具体的数,也可以是单项式或多项式;任何形式的两数和(或差)的平方都可以运用这个公式计算.
(四)整式的除法
整式的除法关键是掌握好同底数幂的除法和单项式与单项式相除的法则。
1、单项式除以单项式的一般步骤是:——————————————————————————————————————2、多项式除以单项式应转化——————————————————————————。
(五) 因式分解
因式分解与因数分解类似,它与整式乘法的过程恰好相反,我们可以运用整式的乘法得到因式分解的方法,也可以运用整式乘法来检验因式分解的正确性.
1.在运用提取公因式法分解因式时,系数要取多项式的各项系数的最大公约数;字母要取各项都含有的字母(或多项式因式)的最低次幂;
2.多项式的第一项系数是负数时,一般要提出 “-”号,使括号的第一项是正的, 在提出“-”号时,多项式的各项都变号.
3.在因式分解时一般步骤:
①如果多项式的各项有————————,那么先提————————————。
②如果各项没有————————————,那么可以尝试————————来分解;
③如果用上述方法都不能分解,那么可以用————————————来分解。
④分解因式,必须进行到每一个多项式都不能再分解为止.
课内练习:
1、计算下列各式:
(1) (-2)2·(-2)3 ; (2) a2·a4·a3 ; (3) x5·x·(-x)3 ;
(a+b-c)2·(c-a-b)3 5) 100·10n+1·10n-1 ;
(6) (x+2)n-1·(2+x)n+1-(x+2)2n
解题方法:熟记公式是解这类题的前提,当题中幂的底数不同时,必须利用乘法和乘方的意义变形,化成同底数幂;当题目中有加、减、乘混合运算时,应计算同底数幂的乘法,然后再合并同类项.
2、计算下列各式:
(1) [(-2)2]6 ;(2) [(x+y)3]4 ;(3) (a4n)n-1 ;(4) -(y4)2·(y2)3 ;
(5) (-a3)2+(-a2)3-(-a2)·(-a)4 ;(6) x3·x2·x4+(-x4)2+4(-x2)4
3、计算下列各式:
(-3a4)3 ;(2) (a2b3)m ;(3) [(x+y)(x-y)]5 ;(4) (x m+2·y 2n-1)2 ;
(5) (-0.125)8×225 ;(6) (1990)n·()n+1 ;
4、已知22x+1+4x=48,求x的值.
解题方法:解这种有关指数方程的基本方法是,将左右两边变形为两个幂相等的等式,且左右两边幂的底数相同,再根据两个底数相同的幂相等,其指数必定相等列出方程,解这个方程即可.
5、计算:
(1) 3x2y·(-2xy3) (2) (-5a2b3)·(-4b2c)·a2b
(3)[2(a-b)3][-3(a-b)2][-(a-b)] (4) (-3xy)2(-x2y)3·(-yz2)2
(-4xy3)(-xy)3-(x2y3)2 (6) (2xyz2)2·(-xy2z)-(-xyz)3·(5yz)(-3z)
6、计算:
(1) (-2a2)·(3ab2-5ab3) (2) (-2x2y)2(-y2+xy+x3)
3) xn-1(2xn-4xn+1+5xn+3) (4) 2a(-ab-b2)-3ab(4a-2b)
7、已知x+y=4,x-y=6,
求代数式x y(y2+y)-y2(x y+2x)-3x y的值
8、计算:
(3x2-2x-5)(-2x+3) (2) (2x-y)(4x2+2xy+y2)
(3a+2b)2 (4) (x-1)(2x-3)(3x+1)
9、已知(a2+pa+8)与(a2-3a+q)的乘积中不含a3和a2项,求p、q的值.
分析:不含有这个项,即为此项的系数为零,又(a2+pa+8)与(a2-3a+q)的乘积中的a3项是-3a3+pa3=(-3+p)a3, a2项是qa2-3pa2+8a2=(q-3 p+8)a2
例10、计算:
(3+x)(3-x) (2) (x2-y3)(x2+y3) (3) (a3b5+c3d4)(c3d4-a3b5)
(-a-3ab)(-3ab+a) (5) (1-2x)(1+2x)(1+4x2)(1+16x4)
(6) 98×102 (7) (x+y)2(x-y)2-(x-y)(x+y)(x2+y2)
(8) (3+9a)(a-)-3(a-2)(3a+6) (9) x(x2+2x)(x-2)
11、计算:(1)(-0.5a-0.2)2 (2) ()2 (3) (am-bn)2 (4) 982
(5)(1-y)2-(1+y)(-1-y) (6) (x-2y)(x+2y)-(x+2y)2
(m+2)2(m-2)2 ( 8) (a+b-c)(a-b+c) 9) (2x+3y-z)
例13、已知 a+b=2,a b=1 求a2+b2、(a-b)2的值
12、先化简,再求值
,其中a=-5
思路点拨:对于这个混合运算,先算乘方,再算除,后算加减,有括号的先算括号里的
13、对下列多项式进行因式分解:
(1)4x3y+4x2y2+xy3; (2)3x3-12xy2
14、分解因式:
⑴ ⑵
注意:⑴中与是一对相反数,首先要将其底变换成相同,再提取公因式法分解因式;⑵中项的指数是含字母m多项式,在提取公因式法时剩余的的指数是相减得到的差.
15、把下列各式分解因式:
⑴ ⑵ ⑶
⑷ ⑸
16、分解下列因式:
⑴ ⑵
⑶ ⑷
17、把下列各式分解因式:
⑴ ⑵ ⑶ ⑷
18、已知:a,b,c 分别为△ABC的三条边长.求证:
19、 已知:n为正整数,求证:能被30整除.
复习题(课外选用)
A组
1. 计算:
(1) a·a (2) (xy)·(xy) (3) [(-x)]
4) [(-x)] (5) (-2mn) (6) (y3)·(y2).
2. 计算:
(1) (4×10)×(2×10) 2) 2a·3a (3)(-3xy)·(-4yz)
(-2a)·(-5a) (5) (-3x)·(2x-x-1) (6) (x+2)(x+6)
(7) (x-2)(x-6);(8) (2x-1)(3x+2).
3. 计算:
(1) (x+2)(x-2) (2) (m+n)(m-n) (3) (-m-n)(-m+n)
(-m-n)(m+n) (5) (-m+n)(m-n) (6) (x+y).
4. 计算:
(1) 2001-2002×2000 (2) (2x+5)-(2x-5) (3) -12xy·3xy-xy·(-3xy)
(4) 2x·(x-1)-3x(x+) (5) (-2x)·(-y)+3xy·(1-x)(6) (-6x)+(-3x)·x.
5. 计算:
(1) a·a÷a (2) (-x)÷(-x)·(-x) (3) 27x÷3x
(4) -12mn÷4mn (5) (6xyz)÷4xy (6) (-6abc)÷(-2ab).
6. 计算:
(1) (6a-4a-2a)÷(-2a) (2) (4xy+6xy-xy)÷2xy
(x+2x-x)÷(-x) (4) (2ab-b)÷2b.
计算: [(x-2y)+(x-2y)(x+2y)-2x(2x-y)]÷2x.
8. 把下列多项式分解因式:
(1) x-25 (2) 2x2y2-4y3z (3) am-an+ap (4) x-25x
(5) 1-4x (6) 25x+20xy+4y (7) x+4x+4x.
9. 先化简,再求值:
(1) 3a(2a-4a+3)-2a(3a+4),其中a=-2;
(a-3b)+(3a+b)-(a+5b)+(a-5b),其中a=-8, b=-6.
一个正方形的边长增加3cm,它的面积增加了45cm.求这个正方形原来的边长.若边长减少3cm,它的面积减少了45cm,这时原来边长是多少呢
11. 1千克镭完全蜕变后,放出的热量相当于3.75×10千克煤放出的热量,据估计地壳里
1×10千克镭.试问这些镭完全蜕变后放出的热量相当于多少千克煤放出的热量.
B组
12. 求下列各式的值:
(1) (3x-2x)÷(-x)-(x-x)·3x,其中x=-;
[(ab+1)(ab-2)-2ab+2]÷(-ab),其中a=, b=-.
已知(x+y)=1, (x-y)=49,求x+y与xy的值.
已知a+b=3, ab=2,求a+b的值.
已知a-b=1, a+b=25,求ab的值.
16. 把下列各式分解因式:
(1) x(x+y)-y(x+y) (2) (a+b)+2(a+b)+1 (3) 4x-4x+x
(4) x-16ax+64a (5) (x-1)(x-3)+1 (6) (ab+a)+(b+1).
课题名称:第14章 勾股定理单元复习教案
复习目标:
1、勾股定理:直角三角形两直角边的平方和等于斜边的平方;
2、如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形;
3、勾股定理能解决直角三角形的许多问题,因此在现实生活和数学中有着广泛的应用.
复习过程:
旧知识回顾(学生交流完成)
1 直角三角形有那些特征?
答: __________________________________________________________________________
2 直角三角形有那些识别方法?
答 : _______________________________________________________________________。
3 你能说几组勾股数呢?
答:_________________________________________________________________________。
合作探究
探究一:如图1,以Rt△的三边为边向外作正方形,其面积分别为,请同学们想一想之间有何关系呢?
1 2
联想
(1)若以Rt△的三边为直径作半圆,其面积分别为,请同学们想一想之间有何关系呢?
(2)若以Rt△的三边为边作等边三角形,其面积分别为,请同学们想一想之间有何关系呢?
2
如图2,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
探究3
.如图3沿AE折叠矩形,点D恰好落在 BC边上的点F处,已知AB =8cm,BC = 10cm,求EC的长.
3 4
探究四 如图4所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是8厘米,则正方形A,B,C,D的面积之和是________平方厘米.
随堂练习
1 在△ABC中,∠C=90°,若 a=5,b=12,则 c=___.
2 在△ABC中,∠C=90°,若c=10,a∶b=3∶4,则ab= .
3 等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___.
4 等边△ABC的高为3cm,以AB为边的正方形面积为___.
5 直角三角形三边是连续整数,则这三角形的各边分别为___.
6. 在Rt△ABC中,斜边AB=2,则AB2+BC2+AC2=______.
7. 在一个直角三角形中,若斜边的长是,一条直角边的长为,那么这个直角三角形的面积是_________.
8. 若三角形的两边长为4和5,要使其成为直角三角形,则第三边长的平方为 .
9. 如图,以三角形三边为直径向外作三个半圆,若较小的两个半圆面积之和等于较大的半圆面积,则这个三角形是_______________三角形.
10、(2006 山西吕梁课改)如图,分别以直角的三边为直径向外作半圆.设直线左边阴影部分的面积为,右边阴影部分的面积和为,则( )
A.
B.
C.
D.无法确定
(四) 你能说说出本章的知识结构吗?
2 本节课有什么收获,请你谈谈?
课外延伸设计
1 国旗杆的绳子垂到地面时,还多了1m,拉着绳子下端离开旗杆5m时,绳子被拉直且下端刚好接触地面,试求旗杆的高.
2 (2006 荆门大纲)园丁住宅小区有一块草坪如图所示,已知米,米,米,米,且,这块草坪的面积是多少?
3 在一棵树的10m高处有两只猴子,其中一只猴子爬下树走到离树20m处的池塘A处,另一只爬到树顶后直接跃向池塘的A处,距离以直线计算,如果两只猴子所经过的距离相等,试问:这棵树有多高
4(10分)如图,四边形ABCD中,∠BAD=90°,∠DBC=90°,AD=3,AB=4,BC=12.
(1)求CD的长;(2)求四边形ABCD的面积.
2
A
-1
0
1
幂的运算
a·a=a a÷a=a
(a)=a (ab)=ab
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
因式分解
提公因式法
公式法
单项式除以单项式
多项式除以单项式
乘法公式(a+b)(a-b)=a-b
(a+b)=a+2ab+b
B
D
C
A
O
A
B
F
C
D
E
A
B
C
直角三角形
勾股定理
应用
判定直角三角形的一种方法
A
D
C
B
学习目标:通过复习,系统掌握本章知识,能运用相关知识解决相关问题,形成技能。
重点:本章知识点。
难点:应用。
一、知识点归纳:
1、概念:
(1)平方根:如果一个数的 等于a,那么这个数叫做a的 。
(2) 叫做a的算术平方根。0的算术平方根是 。
(3)如果一个数的 等于a,那么这个数就叫做a的立方根(也叫做 次方根)
(4)无理数: 叫做无理数. 不能开尽根的根号式及∏都是 。
(5)无理数与有理数统称为 .
(6)开平方:求一个数的 的运算,叫做开平方。
(7)开立方:求一个数的 的运算,叫做开立方。
2、实数的分类:(识记)
3、实数与数轴上的点是 的。
4、法则:
(1)一个正数有两 个平方根,它们互为 ;0的平方根是 ;负数 平方根.
(2)任何数都有 根,正数的立方根是 数,负数的立方根是 数,0的立方根是
二、典型例题:
例1、把下列各数填入相应的大括号内
, -3, 0, 3.1415 , , , , , ,
, 1.121221222122221… (两个1之间依次多个2)
(1)无理数集合: …;
(2)非负数集合: …;
(3)整数集合: …;
(4)分数集合: …。
例2、如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是
A. B. 1.4 C. D.
例3、实数p在数轴上的位置如图所示,
化简______________;
例4、已知数a满足,求a-20002的值。
解:
三、基础练习:(课堂内不能完成的作为课后作业)
1、填空题
(1)的算术平方根是______.
(2)(-)2002·(+)2003=______.
(3)如果=2,那么(x+3)2=______.
(4)若=,那么的值是______.
(5)若xy=-,x-y=5-1,则(x+1)(y-1)=______.
(6)实数a,b在数轴上所对应的点的位置如图所示,则2a___________0,
a+b__________0,-|b-a|________0,化简|2a|-|a+b|=________.
(7)的相反数是______,-的倒数是______.
(8),则x的取值范围是__________.
(9)若的平方根是±3,则a=__________.
(10)当x=__________时,有最小值为__________.
(11)若与|x+y-3|互为相反数,则x=__________,y=__________.
(12)y=+2,则x=__________,y=__________.
2、选择:
(1)的平方根是( )A.3 B.-3 C.± D.
(2)下列说法中正确的是( )
A.任何数都有平方根 B.一个正数的平方根的平方就是它的本身
C.只有正数才有算术平方根 D.不是正数没有平方根
(3) 如果+有意义,那么代数式|x-1|+的值为( )
A.±8 B.8 C.与x的值无关 D.无法确定
(4)下列各式无意义的是( )A.- B. C. D.
(5) 在实数0.3,0,,,0.123456…中,其中无理数的个数是( )
A.2 B.3 C.4 D.5
(6)(-23)2的平方根是( )A.±8 B.8 C.-8 D.不存在
(7)一个自然数的算术平方根是x,则下一个自然数的算术平方根是( )
A.x+1 B.x2+1 C. D.
(8)使有意义的x的值是( )
A.正数 B.负数 C.0 D.非正数
3、计算:
(1)-+. (2)
(3) (4)
4、已知实数满足,求的值.
5、已知实数在数轴上的对应点如图所示,化简
6、已知的小数部分为,求的值。
7、已知某数有两个平方根分别是a+3与2a-15,求这个数
8、已知5+的小数部分为a,5-的小数部分为b,求:a+b的值;
9、已知x,y满足+3,求yx的平方根和算术平方根。
课题名称:13章整式的乘除复习课
知识结构
二、 【方法指导与教材延伸】
(一)同底数幂相乘、幂的乘方、积的乘方同底数幂的除法这四个幂运算,特别是同底数幂相乘的法则是学习整式乘法的基础,其他的如:后面的多项式乘以多项式是转化变成单项式乘以多项式,再转化为单项式乘以单项式,最后转化为同底数幂相乘,所以我们要熟练掌握其法则:
1.同底数幂的相乘的法则是:-------———————————————即用公式表示为:———————————。幂的乘方法则是:—————————————————————即 用公式表示为:————————————————————。积的乘方法则是:———————————————————————— 急用公式表示为:————————
同底数幂的相除的法则是:——————————————————,用公式表示:-————————————————————。
2.其中m、n为正整数,底数a不仅代表具体的数,也可以代表单项式、多项式或其他代数式.
3.幂的乘方法则与同底数幂的相乘的法则有共同之处,即运算中底数不变,但不同之处一个是指数相乘,一个是指数相加
4.这三个幂运算相互容易混淆,出现错误,在初学时要注意辨明“同底数幂”、“幂的乘方”、“积的乘方”等基本概念,对公式的记忆要联系相应的文字表述,运用法则计算时,要注意识别是同底数幂的相乘、幂的乘方还是积的乘方,法则中各字母分别代表什么?再对照法则运算.
(二)整式的乘法
1.单项式与单项式相乘:
由单项式与单项式法则可知,单项式与单项式相乘实为完成三项工作:(1)————————————————————————(2)——————————————(3)——————————————————————,单项式乘法法则对两个以上单项式相乘同样成立。
2.单项式与多项式相乘:
单项式与多项式相乘,实际上是转化为————————————————————,即———————————————————————————用公式表示为—————。
单项式与多项式相乘,结果是多项式,积的项数与因式中多项式的项数相同.
3.多项式与多项式相乘:
多项式与多项式相乘,实际上是先转化为单项式与多项式相乘,即将一个多项式看成一个整体,即(m+n)(a+b)=a(m+n)+b(m+n),再用一次单项式与多项式相乘,得(m+n)(a+b)=ma+n a+m b+b n.
多项式乘以多项式其积仍是多项式,积的次数等于两个多项式的次数之和,积的项数在末合并同类项之前等于两个多项式项数之和.
(三)乘法公式
1.“两数和乘以两数差:————————————————————,用公式表示为:————————————,应用这个乘法公式计算时,应掌握公式的特征:① 公式的左边是两个二项式相乘;并且这两个二项式中有一项是完全相同的项a,另一项是相反数项b;② 公式的右边是相同项的平方a2减去相反数项的平方b2.
公式中的a和b,可以是单项式,也可以是多项式或具体数字.
2.“两数和的平方:————————————————————”.即用公式表示:——————————————————————要理解公式的特征:① 公式的左边是一个二项式的平方,右边是一个二次三项式.公式的适用范围:公式中的a和b可以是具体的数,也可以是单项式或多项式;任何形式的两数和(或差)的平方都可以运用这个公式计算.
(四)整式的除法
整式的除法关键是掌握好同底数幂的除法和单项式与单项式相除的法则。
1、单项式除以单项式的一般步骤是:——————————————————————————————————————2、多项式除以单项式应转化——————————————————————————。
(五) 因式分解
因式分解与因数分解类似,它与整式乘法的过程恰好相反,我们可以运用整式的乘法得到因式分解的方法,也可以运用整式乘法来检验因式分解的正确性.
1.在运用提取公因式法分解因式时,系数要取多项式的各项系数的最大公约数;字母要取各项都含有的字母(或多项式因式)的最低次幂;
2.多项式的第一项系数是负数时,一般要提出 “-”号,使括号的第一项是正的, 在提出“-”号时,多项式的各项都变号.
3.在因式分解时一般步骤:
①如果多项式的各项有————————,那么先提————————————。
②如果各项没有————————————,那么可以尝试————————来分解;
③如果用上述方法都不能分解,那么可以用————————————来分解。
④分解因式,必须进行到每一个多项式都不能再分解为止.
课内练习:
1、计算下列各式:
(1) (-2)2·(-2)3 ; (2) a2·a4·a3 ; (3) x5·x·(-x)3 ;
(a+b-c)2·(c-a-b)3 5) 100·10n+1·10n-1 ;
(6) (x+2)n-1·(2+x)n+1-(x+2)2n
解题方法:熟记公式是解这类题的前提,当题中幂的底数不同时,必须利用乘法和乘方的意义变形,化成同底数幂;当题目中有加、减、乘混合运算时,应计算同底数幂的乘法,然后再合并同类项.
2、计算下列各式:
(1) [(-2)2]6 ;(2) [(x+y)3]4 ;(3) (a4n)n-1 ;(4) -(y4)2·(y2)3 ;
(5) (-a3)2+(-a2)3-(-a2)·(-a)4 ;(6) x3·x2·x4+(-x4)2+4(-x2)4
3、计算下列各式:
(-3a4)3 ;(2) (a2b3)m ;(3) [(x+y)(x-y)]5 ;(4) (x m+2·y 2n-1)2 ;
(5) (-0.125)8×225 ;(6) (1990)n·()n+1 ;
4、已知22x+1+4x=48,求x的值.
解题方法:解这种有关指数方程的基本方法是,将左右两边变形为两个幂相等的等式,且左右两边幂的底数相同,再根据两个底数相同的幂相等,其指数必定相等列出方程,解这个方程即可.
5、计算:
(1) 3x2y·(-2xy3) (2) (-5a2b3)·(-4b2c)·a2b
(3)[2(a-b)3][-3(a-b)2][-(a-b)] (4) (-3xy)2(-x2y)3·(-yz2)2
(-4xy3)(-xy)3-(x2y3)2 (6) (2xyz2)2·(-xy2z)-(-xyz)3·(5yz)(-3z)
6、计算:
(1) (-2a2)·(3ab2-5ab3) (2) (-2x2y)2(-y2+xy+x3)
3) xn-1(2xn-4xn+1+5xn+3) (4) 2a(-ab-b2)-3ab(4a-2b)
7、已知x+y=4,x-y=6,
求代数式x y(y2+y)-y2(x y+2x)-3x y的值
8、计算:
(3x2-2x-5)(-2x+3) (2) (2x-y)(4x2+2xy+y2)
(3a+2b)2 (4) (x-1)(2x-3)(3x+1)
9、已知(a2+pa+8)与(a2-3a+q)的乘积中不含a3和a2项,求p、q的值.
分析:不含有这个项,即为此项的系数为零,又(a2+pa+8)与(a2-3a+q)的乘积中的a3项是-3a3+pa3=(-3+p)a3, a2项是qa2-3pa2+8a2=(q-3 p+8)a2
例10、计算:
(3+x)(3-x) (2) (x2-y3)(x2+y3) (3) (a3b5+c3d4)(c3d4-a3b5)
(-a-3ab)(-3ab+a) (5) (1-2x)(1+2x)(1+4x2)(1+16x4)
(6) 98×102 (7) (x+y)2(x-y)2-(x-y)(x+y)(x2+y2)
(8) (3+9a)(a-)-3(a-2)(3a+6) (9) x(x2+2x)(x-2)
11、计算:(1)(-0.5a-0.2)2 (2) ()2 (3) (am-bn)2 (4) 982
(5)(1-y)2-(1+y)(-1-y) (6) (x-2y)(x+2y)-(x+2y)2
(m+2)2(m-2)2 ( 8) (a+b-c)(a-b+c) 9) (2x+3y-z)
例13、已知 a+b=2,a b=1 求a2+b2、(a-b)2的值
12、先化简,再求值
,其中a=-5
思路点拨:对于这个混合运算,先算乘方,再算除,后算加减,有括号的先算括号里的
13、对下列多项式进行因式分解:
(1)4x3y+4x2y2+xy3; (2)3x3-12xy2
14、分解因式:
⑴ ⑵
注意:⑴中与是一对相反数,首先要将其底变换成相同,再提取公因式法分解因式;⑵中项的指数是含字母m多项式,在提取公因式法时剩余的的指数是相减得到的差.
15、把下列各式分解因式:
⑴ ⑵ ⑶
⑷ ⑸
16、分解下列因式:
⑴ ⑵
⑶ ⑷
17、把下列各式分解因式:
⑴ ⑵ ⑶ ⑷
18、已知:a,b,c 分别为△ABC的三条边长.求证:
19、 已知:n为正整数,求证:能被30整除.
复习题(课外选用)
A组
1. 计算:
(1) a·a (2) (xy)·(xy) (3) [(-x)]
4) [(-x)] (5) (-2mn) (6) (y3)·(y2).
2. 计算:
(1) (4×10)×(2×10) 2) 2a·3a (3)(-3xy)·(-4yz)
(-2a)·(-5a) (5) (-3x)·(2x-x-1) (6) (x+2)(x+6)
(7) (x-2)(x-6);(8) (2x-1)(3x+2).
3. 计算:
(1) (x+2)(x-2) (2) (m+n)(m-n) (3) (-m-n)(-m+n)
(-m-n)(m+n) (5) (-m+n)(m-n) (6) (x+y).
4. 计算:
(1) 2001-2002×2000 (2) (2x+5)-(2x-5) (3) -12xy·3xy-xy·(-3xy)
(4) 2x·(x-1)-3x(x+) (5) (-2x)·(-y)+3xy·(1-x)(6) (-6x)+(-3x)·x.
5. 计算:
(1) a·a÷a (2) (-x)÷(-x)·(-x) (3) 27x÷3x
(4) -12mn÷4mn (5) (6xyz)÷4xy (6) (-6abc)÷(-2ab).
6. 计算:
(1) (6a-4a-2a)÷(-2a) (2) (4xy+6xy-xy)÷2xy
(x+2x-x)÷(-x) (4) (2ab-b)÷2b.
计算: [(x-2y)+(x-2y)(x+2y)-2x(2x-y)]÷2x.
8. 把下列多项式分解因式:
(1) x-25 (2) 2x2y2-4y3z (3) am-an+ap (4) x-25x
(5) 1-4x (6) 25x+20xy+4y (7) x+4x+4x.
9. 先化简,再求值:
(1) 3a(2a-4a+3)-2a(3a+4),其中a=-2;
(a-3b)+(3a+b)-(a+5b)+(a-5b),其中a=-8, b=-6.
一个正方形的边长增加3cm,它的面积增加了45cm.求这个正方形原来的边长.若边长减少3cm,它的面积减少了45cm,这时原来边长是多少呢
11. 1千克镭完全蜕变后,放出的热量相当于3.75×10千克煤放出的热量,据估计地壳里
1×10千克镭.试问这些镭完全蜕变后放出的热量相当于多少千克煤放出的热量.
B组
12. 求下列各式的值:
(1) (3x-2x)÷(-x)-(x-x)·3x,其中x=-;
[(ab+1)(ab-2)-2ab+2]÷(-ab),其中a=, b=-.
已知(x+y)=1, (x-y)=49,求x+y与xy的值.
已知a+b=3, ab=2,求a+b的值.
已知a-b=1, a+b=25,求ab的值.
16. 把下列各式分解因式:
(1) x(x+y)-y(x+y) (2) (a+b)+2(a+b)+1 (3) 4x-4x+x
(4) x-16ax+64a (5) (x-1)(x-3)+1 (6) (ab+a)+(b+1).
课题名称:第14章 勾股定理单元复习教案
复习目标:
1、勾股定理:直角三角形两直角边的平方和等于斜边的平方;
2、如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个三角形是直角三角形;
3、勾股定理能解决直角三角形的许多问题,因此在现实生活和数学中有着广泛的应用.
复习过程:
旧知识回顾(学生交流完成)
1 直角三角形有那些特征?
答: __________________________________________________________________________
2 直角三角形有那些识别方法?
答 : _______________________________________________________________________。
3 你能说几组勾股数呢?
答:_________________________________________________________________________。
合作探究
探究一:如图1,以Rt△的三边为边向外作正方形,其面积分别为,请同学们想一想之间有何关系呢?
1 2
联想
(1)若以Rt△的三边为直径作半圆,其面积分别为,请同学们想一想之间有何关系呢?
(2)若以Rt△的三边为边作等边三角形,其面积分别为,请同学们想一想之间有何关系呢?
2
如图2,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
探究3
.如图3沿AE折叠矩形,点D恰好落在 BC边上的点F处,已知AB =8cm,BC = 10cm,求EC的长.
3 4
探究四 如图4所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是8厘米,则正方形A,B,C,D的面积之和是________平方厘米.
随堂练习
1 在△ABC中,∠C=90°,若 a=5,b=12,则 c=___.
2 在△ABC中,∠C=90°,若c=10,a∶b=3∶4,则ab= .
3 等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___.
4 等边△ABC的高为3cm,以AB为边的正方形面积为___.
5 直角三角形三边是连续整数,则这三角形的各边分别为___.
6. 在Rt△ABC中,斜边AB=2,则AB2+BC2+AC2=______.
7. 在一个直角三角形中,若斜边的长是,一条直角边的长为,那么这个直角三角形的面积是_________.
8. 若三角形的两边长为4和5,要使其成为直角三角形,则第三边长的平方为 .
9. 如图,以三角形三边为直径向外作三个半圆,若较小的两个半圆面积之和等于较大的半圆面积,则这个三角形是_______________三角形.
10、(2006 山西吕梁课改)如图,分别以直角的三边为直径向外作半圆.设直线左边阴影部分的面积为,右边阴影部分的面积和为,则( )
A.
B.
C.
D.无法确定
(四) 你能说说出本章的知识结构吗?
2 本节课有什么收获,请你谈谈?
课外延伸设计
1 国旗杆的绳子垂到地面时,还多了1m,拉着绳子下端离开旗杆5m时,绳子被拉直且下端刚好接触地面,试求旗杆的高.
2 (2006 荆门大纲)园丁住宅小区有一块草坪如图所示,已知米,米,米,米,且,这块草坪的面积是多少?
3 在一棵树的10m高处有两只猴子,其中一只猴子爬下树走到离树20m处的池塘A处,另一只爬到树顶后直接跃向池塘的A处,距离以直线计算,如果两只猴子所经过的距离相等,试问:这棵树有多高
4(10分)如图,四边形ABCD中,∠BAD=90°,∠DBC=90°,AD=3,AB=4,BC=12.
(1)求CD的长;(2)求四边形ABCD的面积.
2
A
-1
0
1
幂的运算
a·a=a a÷a=a
(a)=a (ab)=ab
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
因式分解
提公因式法
公式法
单项式除以单项式
多项式除以单项式
乘法公式(a+b)(a-b)=a-b
(a+b)=a+2ab+b
B
D
C
A
O
A
B
F
C
D
E
A
B
C
直角三角形
勾股定理
应用
判定直角三角形的一种方法
A
D
C
B
同课章节目录
